前言
本章我们介绍随机变量的分布、概率分布特性的刻画以及几个重要的随机变量。
系列文章
1、随机变量
定义2.1:随机变量
设有一概率空间$(\Omega,\mathscr{F},P)$,$X=X(\omega)$是$\Omega=\{\omega_i\}$上的实值函数,如果对任何实数$x$,集合$\{\omega|X(\omega)\leq x\}$属于$\mathscr{F}$,则称$X$是概率空间$(\Omega,\mathscr{F},P)$上的随机变量(简称随机变量)。
这个定义刻画了两个方面的内容:
(1)随机变量$X$是$\omega$的函数,体现了随机而变的特性;
(2)$\{\omega|X(\omega)\leq x\}$是事件,因此可以度量其概率,体现了概率分布的特性。
为了简便考虑,事件$\{\omega|X(\omega)\leq x\}$常简写为$\{X\leq x\}$(或$\{X\in (-\infty,x]\}$)。我们来看一个例子:
一盒中有三个球,两白一黑。从中取出两个球,形式地设函数$X$:取出的白球数。显然这是一个古典概型,我们有:
$$ P(X\leq 1)=P(X=1)=\frac{2}{3},P(X\leq 2)=1 $$
容易看出,函数$X$是一个随机变量,因此类比于随机事件,此处的随机变量通常也可以直观地定义。
2、随机变量的分布函数
2.1:随机变量的分类
随机变量有很多,我们怎么进行研究呢?通常我们将其分为两类:
定义2.2:离散型随机变量
设有一随机变量$X$,若$X$的函数值的个数可数(有限或可数无限),则称$X$为离散型随机变量。
定义2.3:连续型随机变量
设有一随机变量$X$,如果存在非负函数$p(x)$使得对于任意的$a<b,a,b\in\mathbb{R}$有:
$$ P(a<X<b)=\int_{a}^b p(x)\text d x $$
则称$X$为连续型随机变量。
说明
我们这里介绍的两类随机变量并不包含所有情况,也就是说存在既非离散型又非连续型的随机变量,详见教材94页例4.1。
2.2:概率函数:PDF
我们知道,随机变量具有概率分布的特性,显然地,根据两类随机变量的定义,概率函数已经呼之欲出了。
定义2.4:离散型随机变量的概率函数
设有一随机变量$X$,若它是离散型的也即$X$有可数个可能值$x_1,x_2\cdots$,记函数$p_X(k)=P(X=x_k)$,称其为$X$的概率函数,简记为$p_k$。在$X$的取值较少时,通常将所有$x_k$与对应的$p_k$列成一个表,故而我们通常称离散型随机变量的概率函数为分布列或分布律。
定义2.5:连续型随机变量的概率函数
设有一随机变量$X$,若它是连续型的,即存在非负函数$p(x)$使得对于任意的$a<b,a,b\in\mathbb{R}$有:
$$ P(a<X<b)=\int_{a}^b p(x)\text d x $$
此时我们称函数$p(x)$为$X$的概率函数或概率密度函数。
定理2.1:概率函数的性质
(1)非负:$p_k,p(x)\geq 0$
(2)可加性、归一化:$\sum\limits_k p_k,\int_{-\infty}^{+\infty} p(x)=1$
对于连续型随机变量的PDF,由积分的性质可知:
(3)$\forall a\in\mathbb{R},p(a)=0$
(4)$\forall a\in\mathbb{R}$,将$p(a)$改成任意非负数后,$p(x)$仍不变
2.3:分布函数:CDF
定义2.6:随机变量的分布函数
设有一随机变量$X=X(\omega)$,则称函数:
$$ F(x)=P(X\leq x), x\in\mathbb{R} $$
为$X$的(累积)分布函数(CDF),有时也记为$F_X(x)$。
定理2.2:分布函数的性质
(1)非减性:若$a<b$,则$F(a)\leq F(b)$
(2)$\lim\limits_{x\to -\infty} F(x)=0,\lim\limits_{x\to +\infty} F(x)=1$
(3)右连续性:$\lim\limits_{\delta\to 0^+}F(x+\delta)=F(x)$
2.4:概率函数与分布函数的关系
定理2.3:
从PDF到CDF我们有:
$$ F_X(x)=\begin{cases} \sum\limits_{k:k\leq x} p_k,&X为离散型;\\ \int_{-\infty}^x p(u)\text d u,&X为连续型 \end{cases} $$
而从CDF到PDF我们有什么结论呢?
定理2.4:
设$X$为离散型随机变量,则:
$$ p_k=P(X=x_k)=\color{Red}{F_X(x_k+0)-F_X(x_k-0)} $$
定理2.5:
设有一随机变量$X=X(\omega)$,其分布函数为$F(x)$,若$F'(x)$处处存在,则$X$为连续型随机变量,且$F'(x)$就是$X$的概率密度函数。
定理2.6:
设有一随机变量$X=X(\omega)$,其分布函数为$F(x)$且处处连续,$F'(x)$处有限个点$x_1,\cdots,x_n$外存在且连续,则$X$是连续型的,且函数:
$$ p(x)=\begin{cases} F'(x),&x\neq x_i,i=1,\cdots,n\\ a_i,&x=x_i,i=1,\cdots,n \end{cases} $$
($a_i$为任意非负数)为$X$的概率密度函数。
3、重要的随机变量
接下来,我们来研究若干重要的随机变量。同样的,分为离散型与连续型两类。此外我们还将研究随机变量的函数。
3.1:重要的离散型随机变量
(1)两点分布
定义2.7:两点分布(Bernoulli分布)
若$X$的可能值仅有0,1,且:
$$ P(X=1)=p,\ P(X=0)=1-p,\ 0\leq p\leq 1 $$
则称$X$服从两点分布(Bernoulli分布),记为$X\sim B(1,p)$。
这个例子很简单,但是它带给我们的启示是很深刻的。在概率论一:随机事件与概率中我们介绍了样本空间与随机事件,设有一事件$A\subseteq \Omega$,记$P(A)=p$,故而:
$$ X=\begin{cases} 0,&A发生\\ 1,&A不发生 \end{cases} $$
是一个两点分布,这启示我们:可以将研究随机事件概率的问题转化为研究随机变量的问题!
(2)二项分布
定义2.8:二项分布(n重Bernoulli分布)
设随机变量$X$的可能值是$0,1,\cdots,n$,且:
$$ p_k=P(X=k)=\text{C}_{n}^k p^k(1-p)^{n-k},k=0,\cdots,n $$
其中$n\geq 1,0\leq p\leq 1$,则称$X$服从参数为$n,p$的二项分布,记为$X\sim B(n,p)$。
显然地,二项分布的实际背景便是我们在概率论一:随机事件与概率中介绍的$n$重独立试验序列。
定理2.7:二项分布的最大值点
设$X\sim B(n,p)$,则$p_k$在$k=[(n+1)p]$处取得最大值。($[x]$为不超过$x$的最大整数)特别地,若$(n+1)p$为整数,则$p_k$有两个最大值点:$(n+1)p$与$(n+1)p-1$。
(3)几何分布
定义2.9:几何分布
若离散型随机变量$X$的分布律满足:
$$ p_k=P(X=k)=(1-p)^{k-1}p,0<p<1 $$
则称$X$服从参数为$p$的几何分布,记为$X\sim GE(p)$。
由于:
$$ \sum_{k=1}^\infty (1-p)^{k-1}=\frac{1}{1-(1-p)} $$
从而易证$p_k$是归一化的。
几何分布的实际背景为:某人射中靶的概率为$p$,不停射击,则其首次击中靶的次数$X$是服从几何分布的。
(4)超几何分布
定义2.10:超几何分布
若离散型随机变量$X$的分布律满足:
$$ p_k=P(X=k)=\frac{\text{C}_M^k \text{C}_{N-M}^{n-k}}{\text{C}_N^n} $$
(其中$k=0,\cdots,\min \{M,n\}$)则称$X$服从参数为$n,M,N$的超几何分布,记为$X\sim H(n,M,N)$。
超几何分布的实际背景为:设有$N$件产品,$M$件次品,从这$N$件中任选$n$件,取出的次品数为$X$。显然这是一个不放回抽样,而二项分布是放回抽样。容易想到,在产品总数$N\to\infty$时,二者是近似的,因而我们有如下的定理:
定理2.8:
在定义2.10中,设$M=M(N)$,且:
$$ \lim_{N\to \infty} \frac{M(N)}{N}=p,0<p<1 $$
则:
$$ \lim_{N\to\infty} \frac{\text{C}_{M(N)}^k \text{C}_{N-M(N)}^{n-k}}{\text{C}_N^n}=\text{C}_{n}^k p^k(1-p)^{n-k} $$
(5)Poisson分布
定义2.11:Poisson分布
若离散型随机变量$X$的分布律满足:
$$ p_k=P(X=k)=\frac{1}{k!}\lambda^k e^{-\lambda},k=0,1,\cdots $$
则称$X$服从参数为$\lambda$的Poisson分布,记为$X\sim P(\lambda)$。
3.2:重要的连续型随机变量
(1)均匀分布
定义2.12:均匀分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)=\begin{cases} \frac{1}{b-a},&x\in\ [a,b]\\ 0,& else \end{cases}\quad (a<b) $$
则称$X$服从区间$[a,b]$的均匀分布,记为$X\sim U(a,b)$。
(2)指数分布
定义2.13:指数分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)=\begin{cases} \lambda e^{-\lambda x},& x\geq 0\\ 0,&else \end{cases}\quad (\lambda >0) $$
则称$X$服从参数为$\lambda$的指数分布,记为$X\sim E(\lambda)$。
定理2.9:指数分布具有无记忆性
设随机变量$X$非负,则对任意$s,t\geq 0$,等式:
$$ P(X>s+t|X>s)=P(X>t) $$
恒成立的充要条件是$X$服从指数分布。
什么是“无记忆性”呢?设产品寿命服从指数分布,则产品在使用了$s$时间后未寿终的条件下,往后的使用寿命与寿命本身具有相同的概率分布。
(3)正态分布
定义2.14:正态分布(Gaussian分布)
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\sigma>0 $$
则称$X$服从参数为$\mu,\sigma$的正态分布,记为$X\sim N(\mu,\sigma^2)$。
特别地, 若$X\sim N(0,1)$,则称$X$服从标准正态分布,此时$X$的分布函数称为标准正态分布函数,常记为$\Phi(x)$:
$$ \Phi(x)=\int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}\text d u $$
定理2.10:
设有$X\sim N(\mu,\sigma^2)$,则对任意$a<b$:
$$ P(a<X<b)=\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right) $$
定理2.11:
设有$X\sim N(\mu,\sigma^2)$,则对任意$k>0$:
$$ P(\mu-k\sigma<X<\mu+k\sigma)=2\Phi(k)-1 $$
(4)Weibull分布
定义2.15:Weibull分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)={\begin{cases}{\frac {k}{\lambda^k }}x^{k-1}e^{{-(x/\lambda )^{{k}}}},&x\geq 0\\0,&else\end{cases}} $$
则称$X$服从参数为$\lambda,k$的Weibull分布,记为$X\sim W(\lambda,k)$。
当$k=1$时,即是指数分布;当$k=2$时,为Rayleigh分布:
$$ p(x)=\begin{cases}{\frac {x}{\lambda ^{2}}}e^{{-x^{2}/2\lambda ^{2}}},&x\geq 0\\0,&else \end{cases} $$
记为$X\sim R(\lambda)$。
(5) Gamma分布
定义2.16:Gamma分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)= \begin{cases} \frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x},&x>0\\ 0,&else \end{cases} $$
则称$X$服从参数为$\alpha,\beta>0$的Gamma分布,记为$X\sim Ga(\alpha,\beta)$。
(6)Beta分布
定义2.17:Beta分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)= \begin{cases} \frac{1}{\text B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1},&0\leq x\leq 1\\ 0,&else \end{cases} $$
则称$X$服从参数为$\alpha,\beta>0$的Beta分布,记为$X\sim Be(\alpha,\beta)$。
(7)Cauchy分布
定义2.18:Cauchy分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)=\frac{1}{\pi}\cdot \frac{\gamma}{(x-x_0)^2+\gamma^2} $$
则称$X$服从参数为$x_0,\gamma(\gamma>0)$的Cauchy分布,记为$X\sim C(x_0,\gamma)$。当$X\sim C(0,1)$时称$X$服从标准Cauchy分布。
(8)Laplace分布
定义2.19:Laplace分布
若连续型随机变量$X$的概率密度函数满足:
$$ p(x)=\frac{1}{2\beta}e^{\frac{-|x-\alpha|}{\beta}} $$
则称$X$服从参数为$\alpha,\beta(\beta>0)$的Laplace分布,记为$X\sim La(\alpha,\beta)$。
3.3:随机变量的函数
我们在2.3节介绍了分布函数,并在定理2.2中给出了分布函数 三个性质,那么具有这三个性质的函数会是某个随机变量的分布函数吗?此外,我们经常遇到一个随机变量的函数,它具有怎样的分布呢?我们先来研究第二个问题。
定义2.20:随机变量的函数
设有一随机变量$X$,函数$f$有$\text{dom}f\supseteq \{X\leq x\}$,设有一随机变量$Y$,当$X$取值$x$时$Y$的取值有$y=f(x)$。则称$Y$为随机变量$X$的函数。
为了使$Y$满足定义2.1成为一严格定义的随机变量,要求$f$是Borel可测的,见教材95页。由于常见函数均为Borel可测,故本节我们不特别说明。
随机变量函数的一个经典例子是正态分布标准化:设$X\sim N(\mu,\sigma^2)$,则$Y=\frac{1}{\sigma}(X-\mu)$有:$Y\sim N(0,1)$。
定理2.12:随机变量函数的概率密度函数
设有连续型随机变量$X$,概率密度函数$p(x)$,且在区间$(a,b),-\infty\leq a<b\leq +\infty$上有$P(a<X<B)=1$。设有一在$(a,b)$上严格单调的连续函数$f$,其反函数为$g$,且$g$处处可微。随机变量的函数$Y=f(X)$令:
$$ q(y)=\begin{cases} p(g(y))\cdot|g'(y)|,&y\in (\alpha,\beta)\\ 0,&else \end{cases} $$
其中,$(\alpha,\beta)$为反函数$g(y)$的存在区间。则$q(y)$是$Y$的概率密度函数。
练习:$X\sim C(0,1)$,即$p(x)=\left(\pi+\pi x^2\right)^{-1}$,试求随机变量$X$的函数$Y=1-X^{1/3}$的概率密度函数。
定理2.13:随机变量的线性函数
设有随机变量$X$,概率密度函数为$p_X(x)$。若$Y=aX+b,a\neq0$,则$Y$的概率密度函数:
$$ p_Y(y)=\frac{1}{|a|}p_X\left(\frac{y-b}{a}\right) $$
我们再来研究本小节开篇提到的第一个问题。
定义2.21:分布函数的广义反函数
设函数$F(x)$是一分布函数,即满足定理2.2中的三个性质,则称函数:
$$ F^{-1}(y)=\min\{x|F(x)\geq y\} $$
为函数$F(x)$的广义反函数。
定理2.14:广义反函数的性质
(1)$F^{-1}(y)$是$y$的增函数
(2)$F(F^{-1}(y))\geq y$,若$F(x)$在点$x=F^{-1}(y)$处连续,则$F(F^{-1}(y))=y$
(3)$F^{-1}(y)\leq x\Leftrightarrow y\leq F(x)$
定理2.15:
若随机变量$X$的分布函数$F(x)$是连续的,则$X$的函数$Y=F(X)$满足:$Y\sim U(0,1)$。
定理2.16:
设$Y\sim U(0,1)$,$F(x)$是满足定理2.2中三个性质的任意函数,$Y$的函数$X=F^{-1}(Y)$(广义反函数),则$X$的分布函数就是$F(x)$!!
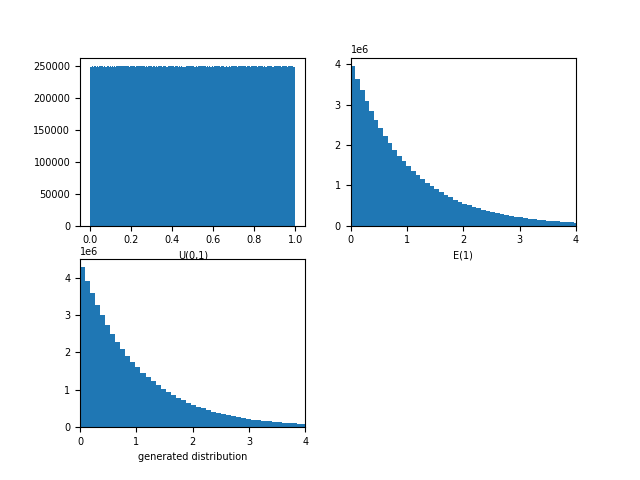
例如:设$Y\sim U(0,1)$,则$X=-\log Y$就有:$X\sim E(1)$!