前言
本章我们介绍优化问题的一般形式与等价、凸优化问题的定义以及几个重要的例子:LP、QP、QCQP等。
系列文章
1、优化问题
1.1:基本概念
我们在第零章中简单介绍了优化问题,我们复习一下。
定义3.1.1.1:优化问题
优化问题的数学表述为:
$$ \begin{align} &\text{minimize}\ \ f_0(\boldsymbol{x})\\ &subject\ to\ f_i(\boldsymbol{x})\leq 0,\ i=1,\cdots,m\\ &\qquad\qquad\ \ h_i(\boldsymbol{x})=0,\ i=1,\cdots,p \end{align}\tag{*} $$
其中我们称:
$\boldsymbol{x}=\left[x_1,\cdots,x_n\right]^\top\in\mathbb{R}^n$称为优化变量;
$f_0:\mathbb{R}^{n}\to\mathbb{R}$称为目标函数或损失(代价)函数,当优化问题为最大化($\max$)时,称$f_0$为效用函数;
$f_i:\mathbb{R}^n\to\mathbb{R}$称为不等式约束函数;
$h_i:\mathbb{R}^n\to\mathbb{R}$称为等式约束函数;
若$m=p=0$,则称问题(*)是无约束优化问题。
关于问题(*),我们还有如下定义:
优化问题的(定义)域$\mathcal{D}$:
$$ \mathcal{D}=\bigcap_{i=1}^m \text{dom}f_i\cap\bigcap_{i=1}^p \text{dom}h_i\cap\text{dom}f_0 $$
可(行)解集$\boldsymbol{X}_f$:$\mathcal{D}$中的满足问题(*)所有约束条件的$\boldsymbol{x}$的集合
问题的最优值$\boldsymbol{p}^{*}$:
$$ \boldsymbol{p}^*=\inf\{f_0(\boldsymbol{x})|\boldsymbol{x}\in\boldsymbol{X}_f\} $$
若$\boldsymbol{X}_f$是空集,规定$\boldsymbol{p}^*=+\infty$
(全局)(最优)解$\boldsymbol{x}^*$:$\boldsymbol{x}^*\in\boldsymbol{X}_f,f(\boldsymbol{x}^*)=\boldsymbol{p}^*$。我们称所有最优解的集合为(最优)解集$\boldsymbol{X}_{opt}$。
$\epsilon$-次优解集$\boldsymbol{X}_\epsilon$:对于很多问题,求解精确的最优解(集)比较困难,我们转而期望求解satisficing solution。显然地,$\boldsymbol{X}_\epsilon$是$f_0$的一个下水平集。
$$ \boldsymbol{X}_\epsilon=\{\boldsymbol{x}|\boldsymbol{x}\in\boldsymbol{X}_f,f_0(\boldsymbol{x})\leq \boldsymbol{p}^*+\epsilon\} $$
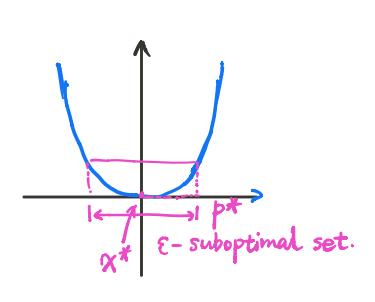
局部最优解:如果存在$r>0$使得:
$$ f_0(\boldsymbol{x})=\inf\{f_0(\boldsymbol{z})|\boldsymbol{z}\in\boldsymbol{X}_f,||\boldsymbol{z}-\boldsymbol{x}||<r\} $$
则称$\boldsymbol{x}$是一个局部最优解。显然,全局最优解$\boldsymbol{x}^*$是一个局部最优解。具体地:
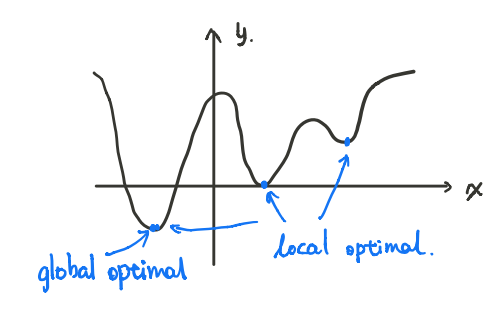
所有局部最优解的集合称为局部最优解集$\boldsymbol{X}_{loc}$。
对于问题(*),有关其“解”的概念有如下关系:
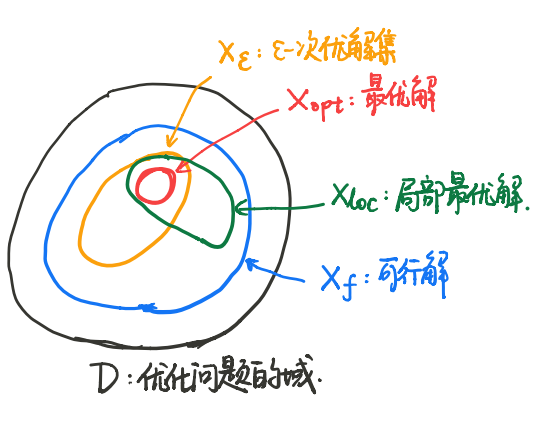
对于可行解集中的任意$\boldsymbol{x}\in\boldsymbol{X}_f$,若约束$f_i(\boldsymbol{x})=0$,则称该约束$f_i$为活动约束(起作用);若$f_i(\boldsymbol{x})<0$,则称约束$f_i$是冗余的(不起作用)。
定义3.1.1.2:可行性问题
有时候我们只期望找到可行解集$\boldsymbol{X}_f$,此时优化问题可写为:
$$ \begin{align} &find\ \boldsymbol{x}\\ &restrictions \end{align} $$
1.2:等价问题
优化问题的等价我们形式地给出下面的定义:
定义3.1.2.1:优化问题的等价
我们说两个优化问题(P1),(P2)是等价的:如果可以通过(P1)的最优解得到(P2)的最优解,反之亦然。显然,这种等价是一个等价关系。
我们考虑如下的若干例子。
(1)缩放
我们沿用问题(*)中的符号,考虑以下优化问题:
$$ \begin{align} &\text{minimize}\ \ \tilde f(\boldsymbol{x})=\alpha_0f_0(\boldsymbol{x})\\ &subject\ to\ \tilde f_i(\boldsymbol{x})=\alpha_if_i(\boldsymbol{x})\leq 0,\ i=1,\cdots,m\\ &\qquad\qquad\ \ \tilde h_i(\boldsymbol{x})=\beta_ih_i(\boldsymbol{x})=0,\ i=1,\cdots,p\\ &where:\ \ \ \ \alpha_i>0,i=0,1,\cdots,m\\ &\qquad\qquad\ \ \beta_i\neq 0,i=1,\cdots,p \end{align}\tag{1} $$
容易知道,问题(1)的可行集、解、最优解必定与(*)的相同,反之亦然,二者是等价的。
(2)变量变换
设有一一映射$\phi:\mathbb{R}^n\to\mathbb{R}^n$,其中$\mathcal{D}\subseteq \phi(\text{dom}\phi)$,我们定义:
$$ \tilde f_i(\boldsymbol{z})=f_i(\phi(\boldsymbol{z})),\ \tilde h_i(\boldsymbol{z})=h_i(\phi(\boldsymbol{z})), $$
则问题:
$$ \begin{align} &\text{minimize}\ \ \tilde f_0(\boldsymbol{z})\\ &subject\ to\ \tilde f_i(\boldsymbol{z})\leq 0,\ i=1,\cdots,m\\ &\qquad\qquad\ \ \tilde h_i(\boldsymbol{z})=0,\ i=1,\cdots,p\\ \end{align}\tag{2} $$
若$\boldsymbol{z}$是(2)的解,自然有$\boldsymbol{x}=\phi(\boldsymbol{z})$是(*)的解,反之也有类似规律。所以(2)与(*)是等价的。
(3)函数变换
设有$\phi:\mathbb{R}\to\mathbb{R}$是单增的;$\phi_1,\cdots,\phi_m:\mathbb{R}\to\mathbb{R}$有$\phi_i(u)\leq0\Leftrightarrow u\leq0$;$\psi_1,\cdots,\psi_p:\mathbb{R}\to\mathbb{R}$有$\psi_i(u)=0\Leftrightarrow u=0$,则问题:
$$ \begin{align} &\text{minimize}\ \ \tilde f(\boldsymbol{x})=\phi_0(f_0(\boldsymbol{x}))\\ &subject\ to\ \tilde f_i(\boldsymbol{x})=\phi_i(f_i(\boldsymbol{x}))\leq 0,\ i=1,\cdots,m\\ &\qquad\qquad\ \ \tilde h_i(\boldsymbol{x})=\psi_i(h_i(\boldsymbol{x}))=0,\ i=1,\cdots,p\\ \end{align}\tag{3} $$
(3)与(*)是等价的。事实上,二者可行解集与最优解均是相同的。
例如:无约束问题$\min ||\boldsymbol{Ax}-\boldsymbol{b}||_2$与$\min ||\boldsymbol{Ax}-\boldsymbol{b}||^2_2$是等价的
(4)消除等式约束
我们先考虑p个等式约束:$\{h_i(\boldsymbol{x})=0,i=1,\cdots,n\}$,设有一些$\boldsymbol{z}\in\mathbb{R}^k$与映射$\phi:\mathbb{R}^k\to\mathbb{R}^n$使得$\boldsymbol{x}=\phi(\boldsymbol{z})$满足这些等式约束,从而问题:
$$ \begin{align} &\text{minimize}\ \ \tilde f_0(\boldsymbol{z})=f_0(\phi(\boldsymbol{z}))\\ &subject\ to\ \tilde f_i(\boldsymbol{z})=f_i(\phi(\boldsymbol{z}))\leq 0,\ i=1,\cdots,m\\ \end{align}\tag{4} $$
与问题(*)是等价的。因为(4)的最优解若为$\boldsymbol{z}^*$,则$\phi(\boldsymbol{z}^*)$必为(*)的最优解,反之也有类似结论。
(5)松弛变量
我们沿用问题(*)中的符号,考虑以下优化问题:
$$ \begin{align} &\text{minimize}\ \ f_0(\boldsymbol{x})\\ &subject\ to\ f_i(\boldsymbol{x})+s_i= 0,\ i=1,\cdots,m\\ &\qquad\qquad\ \ h_i(\boldsymbol{x})=0,\ i=1,\cdots,p\\ &where:\ \ \ \ s_i\geq 0,\ i=1,\cdots,m \end{align}\tag{5} $$
注意该问题的变量包括$(\boldsymbol{x},\boldsymbol{s})$共$n+m$个,$s_i$称为松弛变量。如果$\boldsymbol{x}^*$是问题(*)的最优解,那么 $(\boldsymbol{x}^*,\boldsymbol{s}^*)$ 是(5)的最优解,其中$s_i=-f_i(\boldsymbol{x})$;反之 $(\boldsymbol{x}^*,\boldsymbol{s}^*)$ 是(5)的最优解,那么 $\boldsymbol{x}^*$ 是(*)的最优解。从而可知问题(*)与(5)等价。
2、凸优化问题
2.1:凸优化问题的一般形式
定义3.2.1.1:凸优化问题
若一优化问题形如:
$$ \begin{align} &\text{minimize}\ \ f_0(\boldsymbol{x})\\ &subject\ to\ f_i(\boldsymbol{x})\leq0,\ i=1,\cdots,m\\ &\qquad\qquad\ \ \boldsymbol{a}_i^\top\boldsymbol{x}=b_i,\ i=1,\cdots,p\\ \end{align}\tag{6} $$
若$f_0,f_1,\cdots,f_m$均为凸函数,则称问题(6)为凸优化问题。换句话说,凸优化问题具有条件:
- 目标函数是凸函数
- 不等式约束函数是凸函数
- 等式约束函数$h_i(\boldsymbol{x})=\boldsymbol{a}_i^\top\boldsymbol{x}-b_i$是仿射函数
定义3.2.1.2:拟凸问题与非凸问题
对于一个优化问题,不等式约束函数是凸函数,等式约束函数$h_i(\boldsymbol{x})=\boldsymbol{a}_i^\top\boldsymbol{x}-b_i$是仿射函数,若目标函数$f_0$是拟凸函数而非凸,则称该问题为拟凸问题;若$f_0$是凹函数,则称该问题为非凸问题。
注意!拟凸问题后两个条件也要满足!只是目标函数从凸函数变为了拟凸函数。
2.2:凸优化问题的性质
定理3.2.2.1:凸问题的域与可行解集为凸集
对于一个凸优化问题,其定义域:
$$ \mathcal{D}=\text{dom}f_0\cap\left(\bigcap_{i=1}^m \text{dom}f_i\right) $$
显然是凸集。其可行解集$\boldsymbol{X}_f$是$\mathcal{D}$、m个下水平集($f_i(\boldsymbol{x})\leq 0$)与p个超平面($\boldsymbol{a}^\top\boldsymbol{x}=\boldsymbol{b}_i$)的交集,显然其是一个凸集。
定理3.2.2.2:凸问题的局部最优等于全局最优
对于一个凸问题,其一个局部最优解必为全局最优解。
我们回顾一下局部最优的概念:存在$r>0$使得:
$$ f_0(\boldsymbol{x})=\inf\{f_0(\boldsymbol{z})|\boldsymbol{z}\in\boldsymbol{X}_f,||\boldsymbol{z}-\boldsymbol{x}||<r\} $$
则称$\boldsymbol{x}$是一个局部最优解。现在假设$x$不是全局最优,即$\exists\boldsymbol{y}\in\boldsymbol{X}_f$,使得$f_0(\boldsymbol{y})<f_0(\boldsymbol{x})$。显然$||\boldsymbol{y}-\boldsymbol{x}||_>r$。取:
$$ \boldsymbol{z}=(1-\theta)\boldsymbol{x}+\theta\boldsymbol{y},\ \theta=\frac{r}{2||\boldsymbol{y}-\boldsymbol{x}||}\in(0,\frac{1}{2}) $$
则$\boldsymbol{z}$为$\boldsymbol{x},\boldsymbol{y}$的一个凸组合,由于$\boldsymbol{X}_f$是凸集,从而$\boldsymbol{z}\in\boldsymbol{X}_f$,且对于凸函数$f_0$,有:
$$ f_0(\boldsymbol{z})\leq (1-\theta)f_0(\boldsymbol{x})+\theta f_0(\boldsymbol{y})<f_0(\boldsymbol{x}) $$
同时注意到$||\boldsymbol{z}-\boldsymbol{x}||=\theta||\boldsymbol{x}-\boldsymbol{y}||=\frac{R}{2}$,所以$f_0(\boldsymbol{x})\leq f_0(\boldsymbol{z})$,这与上式是矛盾的。
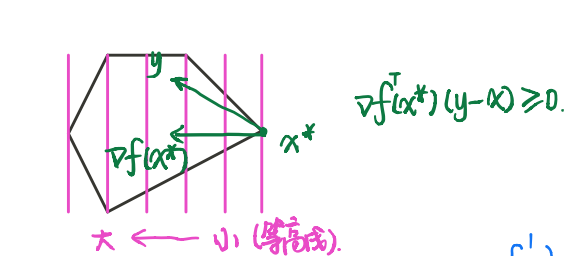
定理3.2.2.3:目标函数可微情况下的最优解判定
对于一凸优化问题,若目标函数$f_0$可微,则一可行解$\boldsymbol{x}^*\in\boldsymbol{X}_f$是最优解当且仅当:
$$ \boldsymbol{J}(\boldsymbol{y}-\boldsymbol{x}^*)\geq0,\forall \boldsymbol{y}\in\boldsymbol{X}_f $$
其中,$\boldsymbol{J}$为$f_0$在$\boldsymbol{x}^*$处的Jacobian矩阵。我们可以用下图来理解该判定:
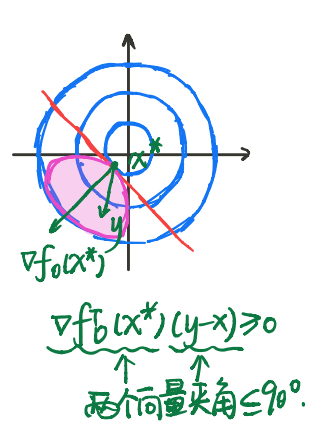
其中,红色部分为可行解集。
2.3:典型的凸优化问题
(1)LP:线性规划
定义3.2.3.1:LP问题的一般形式
设有一优化问题:
$$ \begin{aligned} \min \ & \boldsymbol{c}^T\boldsymbol{x}+d,\boldsymbol{c}\in \mathbb{R}^n,d\in \mathbb{R} \\ s.t. \ & \boldsymbol{Gx}\preccurlyeq \boldsymbol{h},\boldsymbol{G}\in \mathbb{R}^{m\times n},\boldsymbol{h}\in \mathbb{R}^m \\ &\boldsymbol{Ax}=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k \end{aligned}\tag{7} $$
亦即当目标函数与约束函数均为线性时,称为线性规划问题。显然,LP问题(7)的可行解集$\boldsymbol{X}_f$是一个多面体,特别地,在$n=2$时我们可以用等高线去刻画问题(7):
我们注意到,LP问题的最优解一定在边界上,事实上这便是单纯形法的来源。
定义3.2.3.2:LP问题的标准形式
我们称形如(8)式的LP问题为LP的标准形式:
$$ \begin{aligned} \min \ & \boldsymbol{c}^T\boldsymbol{x},\boldsymbol{c}\in \mathbb{R}^n \\ s.t. \ & \boldsymbol{Ax}=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ & \boldsymbol{x}\succcurlyeq \boldsymbol{0} \end{aligned}\tag{8} $$
定义3.2.3.3:LP问题的不等式形式
我们称形如(9)式的LP问题为LP的不等式形式,它没有等式约束:
$$ \begin{aligned} \min \ & \boldsymbol{c}^T\boldsymbol{x},\boldsymbol{c}\in \mathbb{R}^n \\ s.t. \ & \boldsymbol{Ax}\preccurlyeq\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ \end{aligned}\tag{9} $$
定理3.2.3.1:将一般形式的LP转化为标准形式
我们介绍一个将一般形式的LP转化为标准形式的技巧。首先对一般LP引入松弛变量$\boldsymbol{s}$:
$$ \begin{aligned} \min \ & \boldsymbol{c}^T\boldsymbol{x}+d,\boldsymbol{c}\in \mathbb{R}^n,d\in \mathbb{R} \\ s.t. \ & \boldsymbol{Gx}+\boldsymbol{s}=\boldsymbol{h},\boldsymbol{G}\in \mathbb{R}^{m\times n},\boldsymbol{s},\boldsymbol{h}\in \mathbb{R}^m \\ &\boldsymbol{Ax}=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ & \boldsymbol{s}\succcurlyeq \boldsymbol{0} \end{aligned} $$
而后我们将$\boldsymbol{x}$的所有正分量与负分量分别提取出来,将$\boldsymbol{x}$表示为两个非负向量的差,例如:
$$ \boldsymbol{x}= \begin{bmatrix} 1\\ -1\\ 2 \end{bmatrix}= \underbrace{\begin{bmatrix} 1\\ 0\\ 2 \end{bmatrix}}_{\boldsymbol{x}^+}-\underbrace{\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}}_{\boldsymbol{x}^-} $$
从而有优化问题:
$$ \begin{aligned} \min \ & \boldsymbol{c}^T\boldsymbol{x}^+-\boldsymbol{c}^\top\boldsymbol{x}^-+d,\boldsymbol{c}\in \mathbb{R}^n,d\in \mathbb{R} \\ s.t. \ & \boldsymbol{Gx}^+-\boldsymbol{Gx}^-+\boldsymbol{s}=\boldsymbol{h},\boldsymbol{G}\in \mathbb{R}^{m\times n},\boldsymbol{s},\boldsymbol{h}\in \mathbb{R}^m \\ &\boldsymbol{Ax}^+-\boldsymbol{Ax}^-=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ & \boldsymbol{s},\boldsymbol{x}^+,\boldsymbol{x}^-\succcurlyeq \boldsymbol{0} \end{aligned} $$
它的优化变量是$(\boldsymbol{x}^+,\boldsymbol{x}^-,\boldsymbol{s})$,就这个意义上而言它是标准的LP问题。
最后我们来看一个例子:线性分式规划。问题:
$$ \begin{aligned} \min \ & f_0(\boldsymbol{x}) \\ s.t. \ & \boldsymbol{Gx}\preccurlyeq\boldsymbol{h},\boldsymbol{G}\in \mathbb{R}^{m\times n},\boldsymbol{h}\in \mathbb{R}^m \\ &\boldsymbol{Ax}=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ \end{aligned}\tag{P1} $$
其中$f_0$为一线性分式函数:
$$ f_0(\boldsymbol{x})=\frac{\boldsymbol{c}^\top\boldsymbol{x}+d}{\boldsymbol{e}^\top\boldsymbol{x}+f} $$
$\text{dom}f_0=\{\boldsymbol{x}|\boldsymbol{e}^\top\boldsymbol{x}+f>0\}$。由第二章凸函数4.3节例(4)可知,$f_0$不一定凸但是一定拟凸。我们假设(P1)的可行集是非空的。而事实上,我们可以将这一个拟凸问题(P1)转化为一等价的LP问题(P2):
$$ \begin{aligned} \text{min} \ & \boldsymbol{c}^\top\boldsymbol{y}+dz,\boldsymbol{y}\in\mathbb{R}^n,z\in\mathbb{R} \\ s.t. \ & \boldsymbol{Gy}-\boldsymbol{h}z\preccurlyeq \boldsymbol{0},\boldsymbol{G}\in \mathbb{R}^{m\times n},\boldsymbol{h}\in \mathbb{R}^m \\ &\boldsymbol{Ay}-\boldsymbol{b}z=\boldsymbol{0},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ where:\ &\boldsymbol{e}^\top\boldsymbol{y}+fz=1\\ &z\geq 0 \end{aligned}\tag{P2} $$
下面我们来证明(P1)与(P2)等价。由于从最优解等价的角度证明问题等价比较困难,我们采用以下的证明方法:
(1)对于(P1)的一个可行解$\boldsymbol{x}$,可构造(P2)的一个可行解$(\boldsymbol{y},z)$且此时两个问题的目标函数值相同;
(2)对于(P2)的一个可行解$(\boldsymbol{y},z)$,可构造(P1)的一个可行解$\boldsymbol{x}$且此时两个问题的目标函数值相同;
显然这是一个比判断最优解等价更强的判定。下面我们先来看(1)。设$\boldsymbol{x}$对于问题(P1)可行,取:
$$ \boldsymbol{y}=\frac{\boldsymbol{x}}{\boldsymbol{e}^\top\boldsymbol{x}+f},z=\frac{1}{\boldsymbol{e}^\top\boldsymbol{x}+f} $$
可以证明,此时$(\boldsymbol{y},z)$满足问题(P2)的约束条件,且(P2)的目标函数值等于(P1)的目标函数值。
现在设$(\boldsymbol{y},z)$对于问题(P2)可行,若$z>0$则取$\boldsymbol{x}=\boldsymbol{y}/z$,容易证明约束满足且目标函数值相等。下设$z=0$。我们另取(P1)的一个可行解$\boldsymbol{x}_0$,我们现在来考察$\boldsymbol{x}=\boldsymbol{x}_0+t\boldsymbol{y},\forall t\in\mathbb{R}\geq 0$。我们知道:
$$ \boldsymbol{Gy}\preccurlyeq\boldsymbol{0},\boldsymbol{Ay}=\boldsymbol{0},\boldsymbol{e}^\top\boldsymbol{y}=1 $$
而对于(P1)中的约束,我们有:
$$ \begin{align} \boldsymbol{Gx}&=\boldsymbol{Gx}_0+t\boldsymbol{Gy}\preccurlyeq \boldsymbol{0}\\ \boldsymbol{Ax}&=\boldsymbol{Ax}_0+t\boldsymbol{Ay}=\boldsymbol{0}\\ \boldsymbol{e}^\top\boldsymbol{x}+f&=\underbrace{\boldsymbol{e}^\top\boldsymbol{x}_0+f}_{>0}+\underbrace{t\boldsymbol{e}^\top\boldsymbol{y}}_{=t}>t \end{align} $$
所以可知$\boldsymbol{x}$对于问题(P1)是可行的。又:
$$ f_0(\boldsymbol{x})=f_0(\boldsymbol{x}_0+t\boldsymbol{y})=\frac{\boldsymbol{c}^\top\boldsymbol{x}_0+t\boldsymbol{c}^\top\boldsymbol{y}+d}{\boldsymbol{e}^\top\boldsymbol{x}_0+\underbrace{t\boldsymbol{e}^\top\boldsymbol{y}}_t+f}\overset{t\to\infty}{=}\boldsymbol{c}^\top\boldsymbol{y} $$
命题得证。
(2)QP:二次规划
定义3.2.3.4:QP问题的形式
设有一优化问题:
$$ \begin{aligned} \min \ & \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Px}+\boldsymbol{q}^\top\boldsymbol{x}+r,\boldsymbol{q}\in\mathbb{R}^n,r\in\mathbb{R} \\ s.t. \ & \boldsymbol{Gx}\preccurlyeq \boldsymbol{h},\boldsymbol{G}\in \mathbb{R}^{m\times n},\boldsymbol{h}\in \mathbb{R}^m \\ &\boldsymbol{Ax}=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k \end{aligned}\tag{10} $$
而当$\boldsymbol{P}$半正定时,问题(10)是一个凸问题,此时我们称其为二次规划问题。
QP问题的可行集仍为一多面体,而对于目标函数的等高线,LP问题是一组平行的线,QP问题是一组同心的椭圆。此时最优解不一定在边界上了,可能在可行集的内部。
(3)QCQP:二次约束二次规划
定义3.2.3.5:QCQP问题的形式
设有一优化问题:
$$ \begin{aligned} \min \ & \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Px}+\boldsymbol{q}^\top\boldsymbol{x}+r,\boldsymbol{q}\in\mathbb{R}^n,r\in\mathbb{R} \\ s.t. \ & \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{P}_i\boldsymbol{x}+\boldsymbol{q}_i^\top\boldsymbol{x}+r_i\leq 0,\boldsymbol{q}_i\in\mathbb{R}^n,r_i\in\mathbb{R} \\ &\boldsymbol{Ax}=\boldsymbol{b},\boldsymbol{A}\in \mathbb{R}^{k\times n},\boldsymbol{b}\in \mathbb{R}^k\\ where:\ &\boldsymbol{P},\boldsymbol{P}_i\in\boldsymbol{S}^n_{+},i=1,\cdots,m \end{aligned}\tag{11} $$
即当目标函数与不等式约束函数为二次的,等式约束为线性的时,称为二次约束的二次规划问题。
(4)SDP:半正定规划
定义3.2.3.6:SDP问题的形式
设有一优化问题:
$$ \begin{aligned} \min \ & tr(\boldsymbol{CX}) \\ s.t. \ & tr(\boldsymbol{A}_i\boldsymbol{X})=b_i \\ where:\ &\boldsymbol{X}\in\boldsymbol{S}^n_{+}\\ &\boldsymbol{C},\boldsymbol{A}_i\in\mathbb{R}^{n\times n},b_i\in\mathbb{R} \end{aligned}\tag{12} $$
注意矩阵$\boldsymbol{C}$并不是优化变量。这样一类矩阵空间中的优化问题称为半(正)定规划问题。当优化变量$\boldsymbol{X}$为一向量时,SDP问题有以下的形式:
$$ \begin{aligned} \min \ & \boldsymbol{c}^\top\boldsymbol{x} \\ s.t. \ & \sum_{i=1}^n x_i\boldsymbol{A}_i-\boldsymbol{B}\preceq 0 \\ where:\ &\boldsymbol{x},\boldsymbol{c}\in\mathbb{R}^n\\ &\boldsymbol{A}_i,\boldsymbol{B}\in\boldsymbol{S}^n \end{aligned}\tag{13} $$
其中$\boldsymbol{S}^n\subseteq\mathbb{R}^{n\times n}$代表所有$n$阶对称矩阵的集合。
