前言
本部分我们介绍凸函数的定义、性质、例子以及若干保凸运算。请注意!从现在起,忘记所有关于函数凹凸性的定义、性质与判定,诸如所谓下凸、上凹等等概念!
系列文章
1、凸函数的定义、性质、例子
1.1:凸函数的几个定义
定义 2.1.1.1:基本定义
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,若:
- 定义域是凸集:$\text{dom}f$是凸集
- 凸组合的函数值$\leq$函数值的凸组合:
$$ f(\theta\boldsymbol{x}+(1-\theta)\boldsymbol{y})\leq\theta f(\boldsymbol{x})+(1-\theta)\boldsymbol{y},0\leq\theta \leq1,\tag{1} $$
若不等式(1)对$\boldsymbol{x}\neq\boldsymbol{y}$及 $0<\theta<1$严格成立(等号处处不成立),则称$f$是严格凸的。相应地,若$-f$是凸的、严格凸的,则称$f$ 是凹的、严格凹的。
定义 2.1.1.2:降维
(严格意义上来说不算定义,算一个判定定理)
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,$\text{dom}f$是凸集。若$\forall \boldsymbol{x}\in\text{dom}f,\forall \boldsymbol{v}\in\mathbb{R}^n,\forall t\in\mathbb{R}$,若函数$g:\mathbb{R}\to\mathbb{R}$:
$$ g(t)=f(\boldsymbol{x}+t\boldsymbol{v}),\text{dom}g=\{t|\boldsymbol{x}+t\boldsymbol{v}\in\text{dom}f\} $$
是凸的,则$f$是凸的。
定义理解:在高维空间选择一个起点和任意一个方向来切这个高维函数,切出来的边缘就是一个一维函数,“所有切出来的一维函数是凸的” 等价于 “原来的高维函数是凸的”。
定义 2.1.1.3:一阶条件
设有可微函数$f:\mathbb{R}^n\to\mathbb{R}$,若:
- $\text{dom}f$是凸集
- $f(\boldsymbol{y})\geq f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{y}-\boldsymbol{x})$,其中$\boldsymbol{J}$是$f$在$\boldsymbol{x}$的 Jacobian 矩阵,即是梯度矩阵$\nabla_{\boldsymbol{x}}f(\boldsymbol{x})$的转置。特别地,在一维情况下,有$f(y)\geq f(x)+f'(x)(y-x)$。
可以证明,能用定义 2 证明定义 3 的正确性。
定义 2.1.1.4:二阶条件
设有二阶可微函数$f:\mathbb{R}^n\to\mathbb{R}$,若:
- $\text{dom}f$是凸集
- $\forall \boldsymbol{x}\in\text{dom}f$,$f$在$\boldsymbol{x}$处的 Hessian 矩阵$\boldsymbol{H}[f(\boldsymbol{x})]=\nabla^2_{\boldsymbol{x}}f(\boldsymbol{x})$半正定
1.2:关于凸函数定义的说明
- 在基于 Hessian 矩阵判定凸函数的定义 4 中,$\boldsymbol{H}[f(\boldsymbol{x})]\succ 0$可以得到$f$严格凸,反之则不一定成立!
例如$f(x)=x^4$在$x=0$处
- 在判断函数的凹凸性时,不管基于定义几,定义域一定要是凸集!凹函数的定义域也必须是凸集!
例如$f(x)=x^{-2}$
1.3:几个重要的例子
(1)广义二次函数
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,$\text{dom}f=\mathbb{R}^n$,定义为:
$$ f(\boldsymbol{x})=\frac{1}{2}\boldsymbol{x}^\top\boldsymbol{P}\boldsymbol{x}+\boldsymbol{q}^\top\boldsymbol{x}+r $$
其中$\boldsymbol{P}\in\mathbb{R}^{n\times n},\boldsymbol{q}\in\mathbb{R}^n,r\in\mathbb{R}$,不妨设$\boldsymbol{P}$是对称的。应用我们在这篇文章中介绍的求解 Hessian 矩阵的方法,有$\boldsymbol{H}[f(\boldsymbol{x})]=\boldsymbol{P}$,于是当函数$f$是凸(凹)的当且仅当$\boldsymbol{P}$半正定(半负定),特别地,$f$是严格凸(凹)的当且仅当$\boldsymbol{P}$正定(负定)。
(2)仿射函数
设有仿射函数$f(\boldsymbol{x})=\boldsymbol{Ax}+\boldsymbol{b}$,易知$\boldsymbol{H}[f(\boldsymbol{x})]=\boldsymbol{O}$,故而$f$既是凸函数又是凹函数。
(3)指数函数
函数$f(x)=e^{ax}$,$f''(x)=a^2e^{ax}\geq0$,所以$f$是凸函数
(4)幂函数
函数$f(x)=x^a,x\in\mathbb{R}_+$,$f''(x)=a(a-1)x^{a-2}$,故而当 $0\leq a\leq 1$是$f$ 是凹函数,否则则是凸函数。
(5)对数函数
函数$f(x)=\log{x},x\in\mathbb{R}_+$,$f$是严格凹函数。
(6)$L_p$范数
$L_p$范数的定义如下:
$$ ||\boldsymbol{x}||_p=\left(\sum\limits_{i=1}^n |x_i|^p\right)^\frac{1}{p}(p\geq1),\ ||\boldsymbol{x}||_{\infty}=\max\{x_1,\cdots,x_n\}=\max \boldsymbol{x} $$
可以证明,$L_p$是凸的。例如$L_{\infty}$,设有 $0\leq \theta \leq 1$,则:
$$ \begin{align} ||\theta \boldsymbol{x}+(1-\theta)\boldsymbol{y}||_{\infty}&=\max_{i=1,\cdots,n}\{\theta x_i+(1-\theta)y_i\}\\ &\leq \max_{i=1,\cdots,n}\{\theta x_i\}+\max_{i=1,\cdots,n}\{(1-\theta)y_i\}\\ &=\theta||\boldsymbol{x}||_{\infty}+(1-\theta)||y||_{\infty} \end{align} $$
事实上,满足范数三条定义的任意函数都是凸的。
(7)指数和的对数(log-sum-exp)
函数$f:\mathbb{R}^n\to\mathbb{R}$,其定义为:
$$ f(\boldsymbol{x})=\log(\sum\limits_{i=1}^n e^{x_i}) $$
注意到:
$$ \log{e^{\max \boldsymbol{x}}}\leq f(\boldsymbol{x})\leq \log ne^{\max \boldsymbol{x}} $$
从而:
$$ ||\boldsymbol{x}||_\infty\leq f(\boldsymbol{x})\leq ||\boldsymbol{x}|+\log n $$
所以$f$提供了一个对于$||\boldsymbol{x}||_\infty$的解析逼近。我们再来研究$f$的凹凸性。为了描述简便,我们记向量$\boldsymbol{z}=[e^{x_1},\cdots,e^{x_n}]^\top$,$Z=\sum_{i=1}^n z_i=\sum_{i=1}^n e^{x_i}$。显然地,我们有:
$$ \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}^\top}=\boldsymbol{J}=[\frac{e^{x_1}}{Z},\cdots,\frac{e^{x_n}}{Z}] $$
从而:
$$ \boldsymbol{H}[f(\boldsymbol{x})]_{ij}=\begin{cases} Z^{-2}(-z_iz_j), & if\ i\neq j\\ Z^{-2}(Zz_i-z^2_i),&if\ i=j \end{cases} $$
所以:
$$ \boldsymbol{H}[f(\boldsymbol{x})]=Z^{-2}\left(Z\text{diag}(z_1,\cdots,z_n)-\boldsymbol{z}\boldsymbol{z}^\top\right) $$
考察 Hessian 矩阵的二次型函数:
$$ \begin{align} \boldsymbol{v}^\top\boldsymbol{Hv}&=Z^{-2}(Z\boldsymbol{v}^\top\text{diag}(z_1,\cdots,z_n)\boldsymbol{v}-\boldsymbol{v}^\top\boldsymbol{zz}^\top\boldsymbol{v})\\ &=Z^{-2}\left(\underbrace{\left(\sum\limits_{i=1}^n e^{x_i}\right)}_{Z}\cdot\sum\limits_{i=1}^n e^{x_i}v_i^2-\left(\sum\limits_{i=1}^n v_ie^{x_i}\right)^2\right)\\ &\geq Z^{-2}\left(\sum_{i=1}^n (e^{x_i})^2v^2_i-\left(\sum\limits_{i=1}^n v_ie^{x_i}\right)^2\right)\\ &\geq 0\ \ (\text{Cauchy-Schwarz}) \end{align} $$
所以$f$是凸的。
(8)几何平均
函数$f:\mathbb{R}_+^n\to\mathbb{R}$,即$x_i>0$,$f$定义为:
$$ f(\boldsymbol{x})=\left(\prod\limits_{i=1}^n x_i\right)^{\frac{1}{n}} $$
它是凹函数,证明留做练习。
(9)行列式的对数
函数$f:\boldsymbol{S}^n_{++}\to\mathbb{R}_{+},f(\boldsymbol{X})=\log \det \boldsymbol{X}$。
2、保凸运算
注意!这里的保凸运算指一个凸函数经过某种运算、映射后仍为一凸函数,与第一章凸集部分的保凸运算不同!
2.1:非负加权和
定理 2.2.1.1:非负加权和保凸
设有$m$个$\mathbb{R}^n\to\mathbb{R}$上的凸函数$f_1,\cdots,f_n$,则$f=\sum_{i=1}^n w_if_i,w_i\geq0$也是凸函数。类似地,凹函数的非负加权和也是凹的,严格凸(凹)的非负非零加权和也是严格凸(凹)的。
推而广之,设$f(x,y)$在相对固定$y\in \boldsymbol{A}$后关于$x$是凸的,若有$w(y):\boldsymbol{A}\to\mathbb{R_+}$,则:
$$ g(x)=\int_{\boldsymbol{A}}w(y)f(x,y)\text d y $$
也是凸的。(若积分存在)
2.2:复合仿射映射
定理 2.2.2.1:仿射映射的复合运算保凸
设有$f:\mathbb{R}^n\to\mathbb{R},\boldsymbol{A}\in\mathbb{R}^{n\times m},\boldsymbol{b}\in\mathbb{R}^n,\boldsymbol{x}\in\mathbb{R}^m$,则:
$$ g(\boldsymbol{x})=f(\boldsymbol{Ax}+\boldsymbol{b}) $$
若$f$是凸的,则$g$是凸的;若$f$是凹的,则$g$是凹的。
2.3:逐点最大
定理 2.2.3.1:逐点最大运算保凸
设有凸函数$f_1,f_2$,则函数:
$$ f(\boldsymbol{x})=\max\{f_1(\boldsymbol{x}),f_2(\boldsymbol{x})\} $$
其定义域为$\text{dom}f=\text{dom}f_1\cap\text{dom}f_2$,则$f$仍然是凸函数。推而广之,无限个凸函数的极大值亦为凸函数。具体地,若$\forall \boldsymbol{y}\in\boldsymbol{A}$有$f(\boldsymbol{x},\boldsymbol{y})$关于$\boldsymbol{x}$是凸的,则:
$$ g(\boldsymbol{x})=\sup_{\boldsymbol{y}\in\boldsymbol{A}}f(\boldsymbol{x},\boldsymbol{y}) $$
也是凸的。此时$g(\boldsymbol{x})$也被称为$f$的逐点上确界。
2.4:函数复合
设:$h:\mathbb{R}^k\to \mathbb{R},g:\mathbb{R}^n\to \mathbb{R}^k,f=h\circ g,f:\mathbb{R}^n\to \mathbb{R}$,即 $f(\boldsymbol{x})=h(g(\boldsymbol{x})),\text{dom}f=\{\boldsymbol{x}\in dom(g)|g(\boldsymbol{x})\in dom(h)\}$,$\circ$代表函数的复合。我们来讨论$f$的凹凸性关于$g,h$的凹凸性间的规律。
(1)$k=n=1$
我们首先来看最简单的情况:$f(x)=h(g(x))$,不妨设$h,g$二阶可微,且$\text{dom}f=\text{dom}h=\text{dom}g=\mathbb{R}$。此时$f$是凸的当且仅当$f''\geq0$。对$f$求二阶导得:
$$ f''(x)=h''(g(x))\cdot (g'(x))^2+h'(g(x))\cdot g''(x) $$
因此我们有结论:
定理 2.2.4.1:
| $h$ | $g$ | 结论:$f=h(g(x))$ |
|---|---|---|
| 凸、不降 | 凸 | 凸 |
| 凸、不增 | 凹 | 凸 |
| 凹、不降 | 凹 | 凹 |
| 凹、不增 | 凸 | 凹 |
(2)更一般的情况
我们将(1)中的三个条件均放松:维度$n\geq 1$,定义域$\text{dom}h,\text{dom}g\neq \mathbb{R}^k,\mathbb{R}^n$,$h,g$不处处二阶可微,注意此时$h$仍为标量变元的标量函数。
首先我们来解决定义域的问题。设有函数$\phi:\text{dom}\phi\subseteq\mathbb{R}\to\mathbb{R}$,若它是凸函数,则构造函数:
$$ \tilde{\phi}(\boldsymbol{x})=\begin{cases} \phi(\boldsymbol{x}),&if\ x\in\text{dom}\phi\\ +\infty,&else \end{cases} $$
容易证明,$\tilde{\phi}$也是凸的。通常我们将这种操作称为扩展,所以,凸函数的扩展是保凸的。类似地,对于凹函数,我们将在定义域外的函数值赋为$-\infty$,则此时凹函数的扩展也是凹函数。
我们有结论:
定理 2.2.4.2:
| $h$ | $g$ | 结论:$f=h(g(\boldsymbol{x}))$ |
|---|---|---|
| 凸、$\tilde h$不降 | 凸 | 凸 |
| 凸、$\tilde h$不增 | 凹 | 凸 |
| 凹、$\tilde h$不降 | 凹 | 凹 |
| 凹、$\tilde h$不增 | 凸 | 凹 |
练习:
1.若$g$是凸函数,判断$e^{g(x)}$的凹凸性
2.若$g$是凹函数且$g(x)>0$,判断$\log g(x)$的凹凸性
3.若$g$是凹函数且$g(x)>0$,判断 $1/g(x)$ 的凹凸性
答案:凸、凹、凸
(3)矢量复合
若$g_i:\mathbb{R}^n\to\mathbb{R},h:\mathbb{R}^k\to\mathbb{R}$,现在考虑$f(\boldsymbol{x})=h(g_1(\boldsymbol{x}),\cdots,g_k(\boldsymbol{x}))$,我们有结论:
定理 2.2.4.3:
| $h$ | $g$ | 结论:$f$ |
|---|---|---|
| 凸、在每维分量上不降 | 凸 | 凸 |
| 凸、在每维分量上不增 | 凹 | 凸 |
| 凹、在每维分量上不降 | 凹 | 凹 |
| 凹、在每维分量上不增 | 凸 | 凹 |
练习:
1.$g_i$是凸函数,判断$\log\left(\sum_{i=1}^k e^{g_i(\boldsymbol{x})}\right)$的凹凸性
2.若$g_i$是凹函数且$g(x)>0$,取 $0<p\leq 1$,判断$\left(\sum_{i=1}^k (g_i(\boldsymbol{x}))^p\right)^{1/p}$的凹凸性
3.若$g_i$是凸函数且$g(x)>0$,取$p\leq 1$,判断$\left(\sum_{i=1}^k (g_i(\boldsymbol{x}))^p\right)^{1/p}$ 的凹凸性
答案:凸、凹、凸
2.5:函数的透视
我们首先复习一下透视函数的概念。设有映射$P:\mathbb{R}^{n+1}\to\mathbb{R}^n$,其定义域为:$\text{dom}P=\mathbb{R}^n\times \mathbb{R}_+$,即$P(\boldsymbol{z},t)$,$\boldsymbol{z}\in\mathbb{R}^n,t>0$。若$P(\boldsymbol{z},t)=\boldsymbol{z}/t$,则称$P$为一透视函数。
定义 2.2.5.1:函数的透视
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,则映射$g:\mathbb{R}^{n+1}\to\mathbb{R}$,
$$ g(\boldsymbol{x},t)=tf(\frac{\boldsymbol{x}}{t}) $$
称为函数$f$的透视(函数)。其定义域为:
$$ \text{dom}g=\{(\boldsymbol{x},t)|\frac{\boldsymbol{x}}{t}\in\text{dom}f,t>0\} $$
对于函数的透视运算,我们有结论:
定理 2.2.5.1:函数的透视保凸
若$f$为凸函数,则$g$为凸;若$f$为凹函数,则$g$为凹。
我们来看两个例子。
(1)负对数
考虑$\mathbb{R}_+$上的函数$f(x)=-\log x$,则$f$的透视:
$$ g(x,t)=-t\log \frac{x}{t}=t\log\frac{t}{x}=t\log t-t\log x $$
是凸函数。其中$\text{dom}g=\mathbb{R}^2_{+}$。当然我们也可以基于$\boldsymbol{H}[g]$来判断其凹凸性。
(2)相对熵与 KL 散度
设有$\boldsymbol{u},\boldsymbol{v}\in\mathbb{R}^n_+$,考虑函数:
$$ g(\boldsymbol{u},\boldsymbol{v})=\sum_{i=1}^n u_i \log\frac{u_i}{v_i} $$
由(1)的结论,$g(\boldsymbol{u},\boldsymbol{v})$是一系列负对数的和,它是凸函数。(注意:这里不能用非负加权和解释!)
我们定义函数:
$$ KL(\boldsymbol{u},\boldsymbol{v})=\sum_{i=1}^n \left(u_i \log\frac{u_i}{v_i}-u_i-v_i\right) $$
容易证明它是凸的。由于$KL\geq 0$且当且仅当$\boldsymbol{u}=\boldsymbol{v}$时有$KL=0$,故而常用以衡量两个正向量间的偏差。显然地,若$\boldsymbol{u},\boldsymbol{v}$是归一化的即$\boldsymbol{1}^\top\boldsymbol{u}=\boldsymbol{1}^\top\boldsymbol{v}=1$,例如离散型随机变量的分布,则此时$KL$散度与相对熵等价。
2.6:函数的共轭
定理 2.2.6.1:函数的共轭保凸
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,则其共轭$f^*:\mathbb{R}^n\to\mathbb{R}$定义为:
$$ f^*(\boldsymbol{y})=\sup_{\boldsymbol{x}\in\text{dom}f}(\boldsymbol{y}^\top\boldsymbol{x}-f(\boldsymbol{x})) $$
例如在一维的情况下:
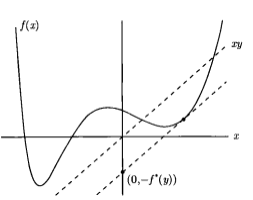
如上图,有函数$f:\mathbb{R}\to\mathbb{R}$以及某一$y\in\mathbb{R}$ ,共轭函数$f^*$是线性函数$yx$和$f(x)$之间的最大差值,见图中虚线所示。显然地,如果$f$一阶可微,在满足$f'(x)=y$的点 处差值最大。
定理2.2.6.2:函数共轭的性质
- 若$f$一阶可微,则$f^*(\boldsymbol{y})$在对应的$\boldsymbol{x}$处必有$\nabla_{\boldsymbol{x}}f(\boldsymbol{x})=\boldsymbol{y}^\top$
- $f^*(\boldsymbol{y})$关于$\boldsymbol{y}$是凸函数,不论$f$是否为凸(因为$f^*(\boldsymbol{y})$是若干关于$\boldsymbol{y}$的仿射函数的逐点上确界)
- Fenchel:
$$ f(\boldsymbol{x})+f^*(\boldsymbol{y})\geq \boldsymbol{x}^\top\boldsymbol{y} $$
若$f$可微,也称为Young不等式。
- 若$f$是闭凸函数,则$f^{**}=f$
我们来看几个函数共轭的例子:
(1)$f(x)=ax+b$
我们设$\text{dom}f=\mathbb{R}$,则其共轭:
$$ \begin{align} f^*(y)&=\sup_{x\in\text{dom}f} (yx-f(x))\\ &=\max_{x\in\mathbb{R}} \{(y-a)x-b\}\\ &=\begin{cases} -b,&y=a\\ +\infty,&else \end{cases} \end{align} $$
(2)$f(x)=-\log x$
$\text{dom}f=\mathbb{R}_+$,其共轭为:
$$ \begin{align} f^*(y)&=\max_{x\in\mathbb{R}_+} \{yx+\log x\}\\ &=\begin{cases} +\infty,&y\geq0\\ -1-\log(-y),&y<0 \end{cases} \end{align} $$
(3)$f(\boldsymbol{x})=\frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Qx}$
$\text{dom}f=\mathbb{R}$,且$\boldsymbol{Q}\in\boldsymbol{S}^n_{++}$。则其共轭:
$$ \begin{align} f^*(\boldsymbol{y})&=\max\{\boldsymbol{y}^\top\boldsymbol{x}-\frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Qx}\}\\ \end{align} $$
由于$f$可微,故而:(参考:矩阵分析二、矩阵微分)
$$ \begin{align} \nabla_{\boldsymbol{x}}(\boldsymbol{y}^\top\boldsymbol{x}-\frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Qx})&=\boldsymbol{y}-\boldsymbol{Qx} \end{align} $$
从而:$\boldsymbol{x}=\boldsymbol{Q}^{-1}\boldsymbol{y}$。将其代回原始表达式,有$f^*(\boldsymbol{y})=\frac{1}{2}\boldsymbol{y}^\top\boldsymbol{Q}^{-1}\boldsymbol{y}$。
3、凸集与凸函数
定义 2.3.1:$\alpha$-下水平集
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,则$f$的$\alpha$-下水平集定义为:
$$ \boldsymbol{C}_\alpha=\{\boldsymbol{x}\in\text{dom}f|f(\boldsymbol{x}\leq\alpha)\} $$
定理 2.3.2:凸函数的所有$\alpha$-下水平集为凸集
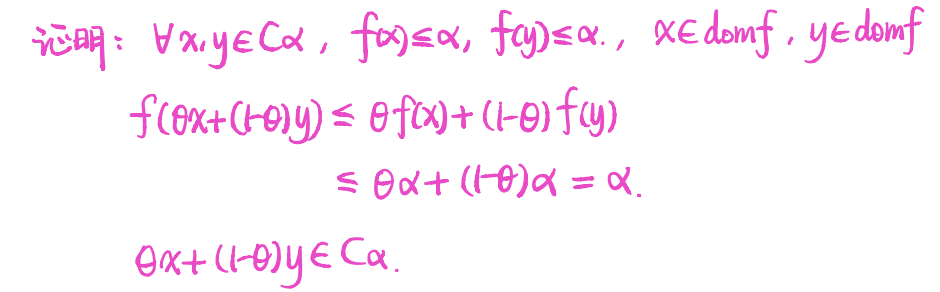
注意,反过来却不一定,即某个函数的所有$\alpha$-下水平集为凸集,其不一定是凸函数。例如$f(x)=-e^x$。
利用$\alpha$-下水平集,对于$f:\mathbb{R}^2\to\mathbb{R}$,我们可以在$\mathbb{R}^2$上用等高线刻画$f$,如下图:
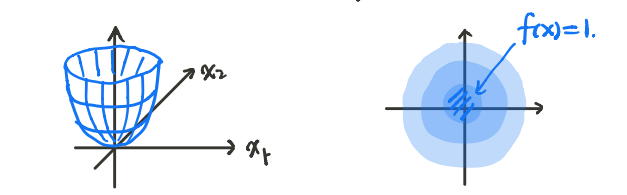
练习:设有$f:\mathbb{R}^2\to\mathbb{R}$,其在$\mathbb{R}^2$上的等高线如下:
试判断其凹凸性。
答案:无法判断!!
类似地,我们可以定义$\alpha$-上水平集:$\{\boldsymbol{x}\in\text{dom}f|f(\boldsymbol{x}\geq\alpha)\}$,可以证明,凹函数的所有$\alpha$-上水平集是凸的。
4、拟凸函数
4.1:拟凸函数的基本定义
定义 2.4.1.1:拟凸函数的基本定义
- 若$f$的所有下水平集为凸集,则称$f$为拟凸函数;
- 若$f$的所有上水平集为凸集,则称$f$为拟凹函数;
- 若$f$既是拟凸函数又是拟凹函数,则称$f$为拟线性函数。
例如:$e^x$是拟线性的
关于定义的说明:
- 容易知道,拟线性函数的定义域和所有水平集:$\{\boldsymbol{x}\in\text{dom}f|f(\boldsymbol{x}=\alpha)\}$是凸集。
- 凸函数一定是拟凸函数,凹函数一定是拟凹函数,反之则不一定。
4.2:拟凸函数的其他等价定义
定义 2.4.2.1:
设有函数$f$,则$f$为拟凸函数当且仅当:$\forall \boldsymbol{x},\boldsymbol{y}\in\text{dom}f,0\leq \theta\leq 1$,有:
$$ f(\theta\boldsymbol{x}+(1-\theta)\boldsymbol{y})\leq \max\{f(\boldsymbol{x},f(\boldsymbol{y}))\} $$
我们知道,凸函数有一阶条件与二阶条件定义,拟凸函数也有类似定义。
定义2.4.2.2:一阶条件
设$f:\mathbb{R}^n\to\mathbb{R}$可微,则$f$拟凸当且仅当:
- $\text{dom}f$为凸集
- $\forall \boldsymbol{x},\boldsymbol{y}\in\text{dom}f,f(\boldsymbol{y})\leq f(\boldsymbol{x})$,有:$\boldsymbol{J}(\boldsymbol{y}-\boldsymbol{x})\leq 0$。其中,$\boldsymbol{J}$为$f$在$\boldsymbol{x}$处的Jacobian矩阵。
定义2.4.2.3:二阶条件
设$f:\mathbb{R}^n\to\mathbb{R}$二阶可微,则$f$拟凸当且仅当:
- $\text{dom}f$为凸集
- $\forall \boldsymbol{y}\in\text{dom}f,\boldsymbol{y}^\top\nabla_{\boldsymbol{x}}f(\boldsymbol{x})\geq 0$,有:$\boldsymbol{y}^\top\boldsymbol{H}[f(\boldsymbol{x})]\boldsymbol{y}\geq 0$。其中,$\boldsymbol{H}[f(x)]$为$f$在$\boldsymbol{x}$处的Hessian矩阵。(注意这里不是$\boldsymbol{H}$正定的意思)
例如:
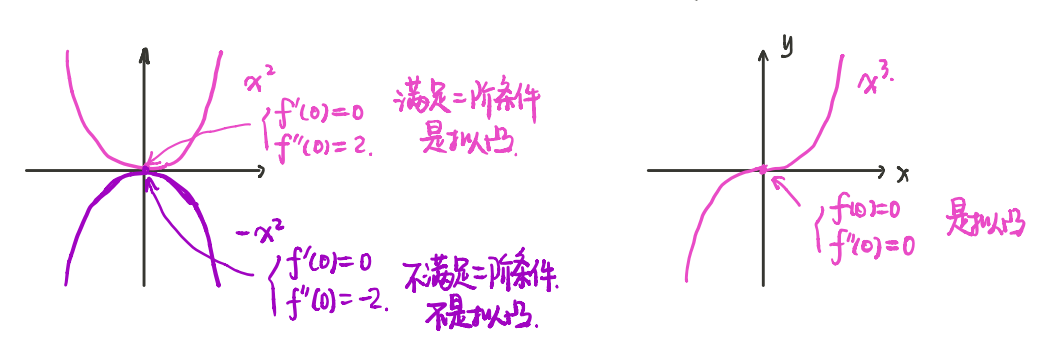
4.3:几个重要的例子
(1)0 范数
我们定义 0 范数$||\boldsymbol{x}||_0$为:$\boldsymbol{x}$中非零元素个数。事实上,0 范数不满足齐次性,它并不是范数。
在一维情况下,容易看出,它不是凸函数,但是拟凸的:
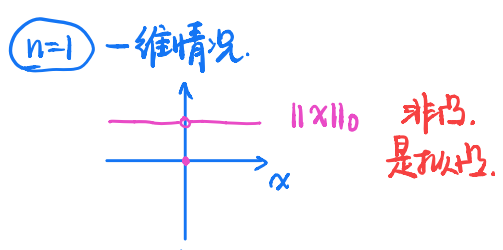
而在二维情况下,其等高线为:
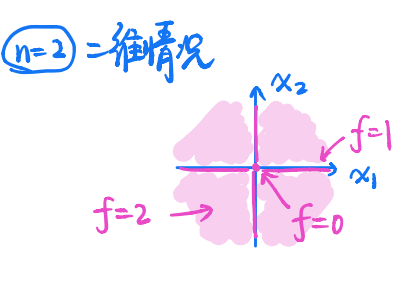
也即当$\boldsymbol{x}=\boldsymbol{0}$时,$f=0$;当$\boldsymbol{x}$为坐标轴上一点时,$f=1$;其余的情况下$f=2$。显然地,1.5-下水平集并不是凸集,所以其不是拟凸的。
(2)$L_1$范数
我们知道,$||\boldsymbol{x}||_1=\sum_{i=1}^n |x_1|$是凸函数,其在 1、2 维情况下的等高线:
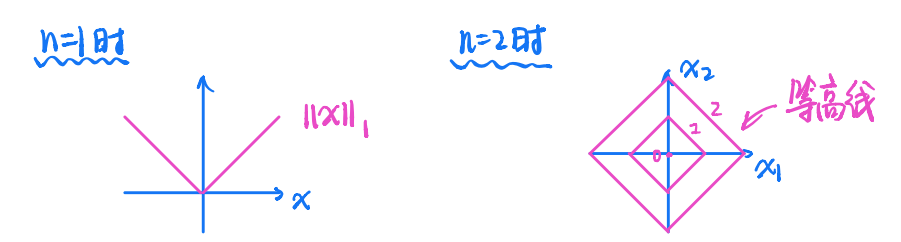
从等高线图我们也可以得知$L_1$范数是拟凸的。
(3)$f(\boldsymbol{x})=\log(\boldsymbol{x}^\top\boldsymbol{x}+1)$
等高线如下:
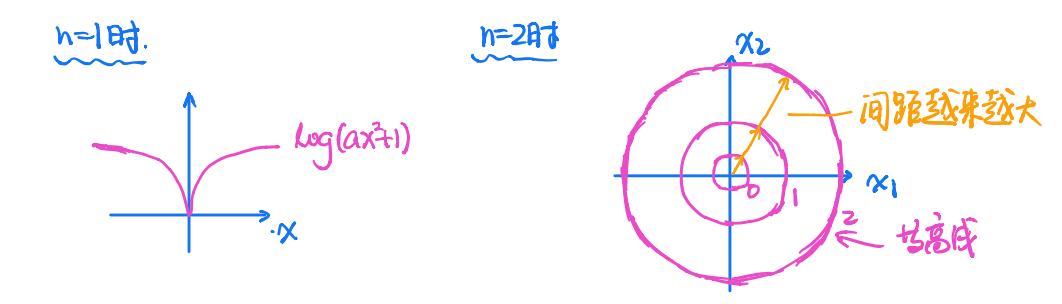
它是拟凸的。
(4)线性分式函数
我们在第一章凸集中介绍了线性分式函数:
$$ f(\boldsymbol{x})=\frac{\boldsymbol{Ax}+\boldsymbol{b}}{\boldsymbol{c}^\top\boldsymbol{x}+d},\ \text{dom}f=\{\boldsymbol{x}|\boldsymbol{c}^\top\boldsymbol{x}+d>0\} $$
当$\boldsymbol{A}$取$\boldsymbol{a}^\top$是为一种特殊情况。我们知道,一个凸集经线性分式函数映射后的像为一凸集,可它是不是凸函数呢?我们来研究线性分式函数的下水平集:
$$ \begin{align} \boldsymbol{C}_\alpha&=\{\boldsymbol{x}|\boldsymbol{c}^\top\boldsymbol{x}+d>0,\frac{\boldsymbol{a}^\top\boldsymbol{x}+b}{\boldsymbol{c}^\top\boldsymbol{x}+d}\leq\alpha\}\\ &=\{\boldsymbol{x}|\boldsymbol{c}^\top\boldsymbol{x}+d>0,(\boldsymbol{a}^\top-\alpha\boldsymbol{c}^\top)\boldsymbol{x}+b-\alpha d\leq 0\} \end{align} $$
显然$\boldsymbol{C}_\alpha$是一个多面体为凸集,从而可知$f$是拟凸的。
5、对数-凸与对数-凹
定义2.5.1:对数-凸、对数-凸
若$f:\mathbb{R}^n\to\mathbb{R}$为凸(凹)函数,且$\forall \boldsymbol{x}\in\text{dom}f,f(\boldsymbol{x})>0$,且$\log f$是凸(凹)函数,则称$f$是对数-凸(对数-凹)的。
定理2.5.1:对数-凸是凸函数
若$f$是对数-凸的,则$f$是凸函数。类似地,非负凹函数是对数+凹函数。
对数-凸一定是拟凸的;对数-凹一定是拟凹的。

1 条评论
感谢你的分享,2.3.1下水平集的定义错了