前言
本文我们介绍几篇关于Adam收敛性的工作。先介绍paper的主要内容,再写remark。比较冗长的证明这里就不展开了。
On the Convergence of Adam and Beyond
Paper
在之前介绍Adam的文章中:
我们提到Adam在在线凸优化的分析框架下无法证明收敛性,这是由于其无法保证:
$$ \Gamma_{k}=\frac{\sqrt{\hat{v}_{i}^{(k)}}}{\eta^{(k-1)}}-\frac{\sqrt{\hat{v}_{i}^{(k-1)}}}{\eta^{(k-1)}}\geq 0\tag{1} $$
恒成立。也即在某些情况下步长并不是单调非增的。Reddi等人指出在拥有少量频次非常低的、梯度却非常大的数据点的数据集上(1)的非恒成立性可能导致严重的不收敛,并构造了几个凸优化问题来说明无论如何调节$\varepsilon,\beta_1,\beta_2$都将导致不收敛。
回顾Adam算法,其参数更新式为:
$$ \begin{align} m^{(\tau)}_i&=\beta_1\cdot m_i^{(\tau-1)}+(1-\beta_1)\cdot g^{(\tau)}_i\\ v^{(\tau)}_i&=\beta_2\cdot v_i^{(\tau-1)}+(1-\beta_1)\cdot \left(g_i^{(\tau)} \right)^2\\ \hat m^{(\tau)}_i &=m^{(\tau)}_i/(1-\beta_1^\tau)\\ \hat v^{(\tau)}_i &=v^{(\tau)}_i/(1-\beta_2^\tau)\\ \theta^{(\tau+1)}_i&=\theta^{(\tau)}_i-\frac{\eta}{\sqrt{\hat v^{(\tau)}_i}+\varepsilon}\cdot \hat m^{(\tau)}_i \end{align}\tag{2} $$
Reddi等人在此之上提出了一种变体算法,从$\hat v^{(\tau)}_i =v^{(\tau)}_i/(1-\beta_2^\tau)$更改为:$\hat v^{(\tau)}_i =\max \{\hat v_i^{(\tau-1)} ,v^{(\tau)}_i/(1-\beta_2^\tau)\}$从而提出了AMSGrad算法:
$$ \begin{align} m^{(\tau)}_i&=\beta_1\cdot m_i^{(\tau-1)}+(1-\beta_1)\cdot g^{(\tau)}_i\\ v^{(\tau)}_i&=\beta_2\cdot v_i^{(\tau-1)}+(1-\beta_1)\cdot \left(g_i^{(\tau)} \right)^2\\ \hat m^{(\tau)}_i &=m^{(\tau)}_i/(1-\beta_1^\tau)\\ \hat v^{(\tau)}_i &=\color{Red}\max \{\hat v_i^{(\tau-1)} ,v^{(\tau)}_i/(1-\beta_2^\tau)\}\\ \theta^{(\tau+1)}_i&=\theta^{(\tau)}_i-\frac{\eta}{\sqrt{\hat v^{(\tau)}_i}+\varepsilon}\cdot \hat m^{(\tau)}_i \end{align}\tag{3} $$
而后同样在在线凸优化分析框架下得出了收敛性的结果(无偏差修正项):
实验方面,首先是说明了构造的凸优化例子Adam确实不收敛,而AMSGrad能正确收敛:
而后是逻辑回归、FCN、CNN的一些实验结果: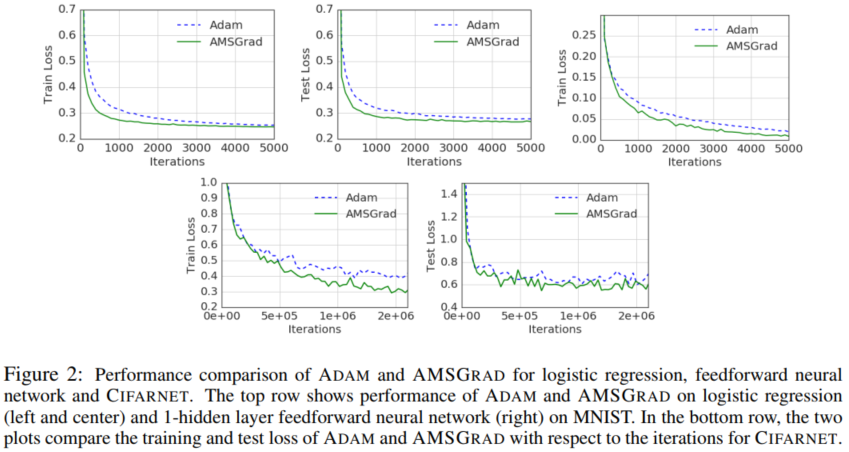
Remark
虽然说这篇文章分很高(9 8 8)而且最后被选为ICLR 2018的best paper,但个人认为这篇文章意义比较有限。
首先我们从理论的角度回顾AMSGrad的心路历程,作者首先在比较极端的情况下证明Adam可能不收敛。我们首先不讨论构造的例子是否有实践意义,这种极端的情况本质上是模拟了含离群点的数据:拥有少量频次非常低的、梯度却非常大的数据点的数据集。感觉在优化算法领域讨论这个问题有些奇怪,我们完全可以通过预处理的手段降低离群点的影响,而且在mini-batch的训练框架下,个人感觉离群点并没有多大影响。而骆梁宸在一篇博客:Adam 究竟还有什么问题 —— 深度学习优化算法概览(二)中也指出:
在作者的构造下,如果去除这些罕见数据点,那么 Adam 会与不去除一样收敛到相同位置;而 AMSGrad (作者提出的新方法) 则会因为罕见数据点是否存在的不同而收敛到完全不同的结果。个人认为这个构造反而是证明了 Adam 比 AMSGrad 更能应对 outlier 值,极端构造下的收敛性,并不意味着什么。
而且论文攻击的是Adam的收敛性分析框架,那么换一种分析框架(例如非凸L-光滑)Adam是不是就能得到收敛的结果呢?Adam的分析框架确实有问题,但据此否定Adam算法本身是牵强的。
其次我们再来看作者的实验,个人认为这是文章问题最大的地方。首先从实验的设置来看只做了LR、FCN和CNN的实验,而且比较的竟然是Training Loss和Test Loss!比较的不应该是测试集的指标么(比如ACC)?说Loss更低就是better performance感觉不太好。而且原文章中去掉了偏差修正项,那实验是不是要做消融呢?感觉实验部分还不太完善。
最后我们来看工程实践中AMSGrad的表现。参考资料2中表明Adam与AMSGrad之间并没有很大的差距。从实践的角度而言,Adam的使用率远远高于AMSGrad。
On the convergence of a class of Adam-type algorithms for non-convex optimization
Paper
文章首先构造了一个自适应算法的统一框架:(Generalized Adam)
$$ \begin{align} m^{(\tau)}_i&=\beta_1\cdot m_i^{(\tau-1)}+(1-\beta_1)\cdot g^{(\tau)}_i\\ \hat v^{(\tau)}_i&=h_\tau(g_i^{(1)},\cdots,g_i^{(\tau)}) \\ \theta^{(\tau+1)}_i&=\theta^{(\tau)}_i-\frac{\eta}{\sqrt{v^{(\tau)}_i}+\varepsilon}\cdot m^{(\tau)}_i \end{align}\tag{4} $$
早期的自适应算法都可以用这个框架表达:
| $v_i^{(\tau)}$\ $\beta_1^{(\tau)}$ | $\beta_1^{(\tau)}\equiv0$ | $\beta_1^{(\tau)}\leq \beta_1^{(\tau-1)}\\ \beta_1^{(\tau)}\overset{t\to\infty}{\to}b\geq0$ | $\beta_1^{(\tau)}\equiv\beta_1$ |
|---|---|---|---|
| $\hat v_i^{(\tau)}\equiv 1$ | SGD | - | HB |
| $\hat v_i^{(\tau)}=\frac 1\tau \sum_{k=1}^\tau \left(g_i^{(k)} \right)^2$ | AdaGrad | AdaFom | AdaFom |
| $\hat v_i^{(\tau)}=\beta_2 v_i^{(\tau)}+(1-\beta_2)\left(g_i^{(\tau)} \right)^2$ | RMSProp | Adam | Adam |
| $v_i^{(\tau)}=\beta_2 v_i^{(\tau)}+(1-\beta_2)\left(g_i^{(\tau)} \right)^2\\ \hat v_i^{(\tau)}=\max\{\hat v_i^{(\tau)},v_i^{(\tau)} \}$ | AMSGrad | AMSGrad | AMSGrad |
而后我们假设$\mathcal L\in \mathcal C_{L}^{1,1}$,$\|\nabla \mathcal L(\boldsymbol{\theta}^{(\tau)}) \|\leq H,\|\boldsymbol{g}^{(\tau)}\|\leq H$,$\boldsymbol{g}^{(\tau)}=\nabla\mathcal L(\boldsymbol{\theta}^{(\tau)})+\boldsymbol{\zeta}^{(\tau)}$且$\mathbb{E}[\boldsymbol{\zeta}]=\boldsymbol{0}$。如果进一步假设$\beta_1^{(\tau)}$非增、$\|\eta^{(\tau)}\boldsymbol{m}^{(\tau)}/\sqrt{\boldsymbol{\hat v}^{(\tau)}} \|\leq G$那么(4)式所示的算法恒有:
$$ \begin{align} \mathbb{E}\left[\sum_{k=1}^\tau \eta^{(k)}\left\langle \nabla\mathcal L(\boldsymbol{\theta}^{(k)}) ,\frac{\nabla \mathcal L(\boldsymbol{\theta}^{(k)})}{\sqrt{\boldsymbol{\hat v}^{(k)}}}\right\rangle \right]\leq &\ \mathbb{E}\left[C_1\underbrace{\sum_{k=1}^\tau\|\frac{\eta^{(k)}\boldsymbol{g}^{(k)} }{\sqrt{\boldsymbol{\hat v}^{(k)}}} \|^2}_{A} +C_2\underbrace{\sum_{k=2}^\tau \|\frac{\eta^{(k)} }{\sqrt{\boldsymbol{\hat v}^{(k)}}}-\frac{\eta^{(k-1)} }{\sqrt{\boldsymbol{\hat v}^{(k-1)}}} \|_1}_{B} \right]\\ & +\mathbb{E}\left[C_3\sum_{k=2}^{\tau-1}\|\frac{\eta^{(k)} }{\sqrt{\boldsymbol{\hat v}^{(k)}}}-\frac{\eta^{(k-1)} }{\sqrt{\boldsymbol{\hat v}^{(k-1)}}}\|^2 \right]+C_4\tag{5} \end{align} $$
如果记(5)式不等式右侧的上界为$O(s_1(\tau))$,记$\gamma_\tau=\min\limits_{i=1,\cdots,d}\min\limits_{k=1,\cdots,\tau}\eta^{(k)}/\sqrt{\hat v_i^{(k)}}$,$\sum_{k=1}^\tau \gamma_k=\Omega(s_2(\tau))$,则:
$$ \min_{k=1,\cdots,\tau}\mathbb{E}[\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(k)})\|^2]=O\left(\frac{s_1(\tau)}{s_2(\tau)} \right)\tag{6} $$
我们首先从直观上进行分析。显然如果$s_1(\tau)=o(s_2(\tau))$($o$表示高阶无穷小)则算法将收敛,如果称$\eta/\sqrt{\hat v_i}$为有效步长(effective stepsize)的话,$\gamma_k$可以理解为有效步长的累计(accumulation of effective stepsizes),(5)式中的B项可以理解为有效步长震荡的累计(accumulation of oscillation of effective stepsizes)。如果震荡太大则会影响$s_1(\tau)$的上界进而导致不收敛,这与AMSGrad中$\Gamma_k$必须大于等于0是类似的。
而在简单函数上进行实验分析,文章指出Adam算法中A、B增长的过快,而AMSGrad算法则较慢,这说明了AMSGrad的收敛性是优于Adam的。
最后文章还据此给出了AMSGrad和AdaFom的收敛速度,这里就不展开了。
Remark
这篇文章的分数为6 7 7,算是比较合适的。文章的问题主要有两点:
- 分析了Adam-Type,却没有分析Adam的收敛性,而是进一步分析了其在一些情况下的非收敛性,而且举的例子是凸函数,这与整篇文章的非凸分析不合。
- 实验只做了MNIST上的CNN,FCN和NLP任务都没做。
当然瑕不掩瑜,在对Adam类算法进行非凸分析的领域内这是比较早的一篇文章了(不知道是不是第一篇),而且后续的很多算法也沿用了本文的分析框架。总体而言是一篇不错的文章。
Towards practical Adam: Non-convexity, convergence theory, and mini-batch acceleration
文章指出,为了保证(或者提高)Adam的理论收敛性,我们可以从以下几个方面入手:
- 步长衰减:也即严格保证$\Gamma_k\geq 0$,这与上述两篇文章的分析是一致的。
- 采用大batch-size:对于确定性优化中,Adam与RMSProp能够收敛;而在随机优化中如果batch-size大到一定程度则Adam也是能收敛的。
References
- On the Convergence of Adam and Beyond,Sashank J. Reddi, Satyen Kale, Sanjiv Kumar,ICLR,2018
- On the convergence of a class of Adam-type algorithms for non-convex optimization,Xiangyi Chen, Sijia Liu, Ruoyu Sun, Mingyi Hong,ICLR 2019,2018
- Experiments with AMSGrad
- Towards practical Adam: Non-convexity, convergence theory, and mini-batch acceleration,Congliang Chen, Li Shen, Fangyu Zou, Wei Liu,JMLR,2022
