前言
本文介绍SGD优化器的参数更新公式并进行简单的编程实践。
回顾GD
在优化器二:Vanilla Gradient Descent一文中我们介绍了经典梯度下降:
我们知道,GD只能求解如下的经验风险最小化问题:
$$ \begin{aligned} \min \ & \mathcal{L}(\boldsymbol{\theta};\boldsymbol{T})=\frac 1N \sum_{i=1}^N L(\boldsymbol{\hat y}_i, \boldsymbol{y}_i) \\ where:\ & \boldsymbol{\theta}\in\boldsymbol{\Theta} \end{aligned}\tag{1} $$
它的参数更新公式为:
$$ {\boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta^{(\tau)} \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta}^{(\tau)} ; \boldsymbol{T}\right)}\tag{2} $$
它可以收敛至一个局部最优。对于凸问题,则可以收敛至全局最优。它在凸问题上次线性收敛,在强凸问题上线性收敛,具体地:
| 条件 | $i(\epsilon)$ | $\epsilon(i)$ | $i_S(\epsilon)$ | 收敛速度 |
|---|---|---|---|---|
| $L$-光滑+凸 | $\Omega(\frac 1\epsilon)$ | $O(\frac{1}{i})$ | $\Omega(\frac 1 {\epsilon^2})$ | 次线性收敛 |
| $L$-光滑+强凸 | $\Omega((\log \frac{1}{\epsilon})/\log \frac{\kappa}{\kappa-1})$ | $O\left((1-\kappa^{-1})^i \right)$ | $\Omega((\log \frac{1}{\epsilon^2})/\log \frac{\kappa}{\kappa-1})$ | 线性收敛 |
但是由于我们需要求解整个数据集上的梯度$\nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta}^{(i-1)} ; \boldsymbol{T}\right)$,以凸问题求解$i(\epsilon)$为例,设$\boldsymbol{x}$是$d$维的,我们有$N$个数据,则总体算法的复杂度$\geq \Omega(Nd\cdot \frac{1}\epsilon)$,也即总体迭代成本与样本数是成正相关的!在数据量比较大时效率很低。而更要命的是GD只能求解ERM问题,为了让ERM的解尽可能地近似期望风险最小化的解,我们的样本量要尽可能大一些!两相矛盾之下,我们需要一种计算效率更高的算法。
问题的简化表示
对于如(1)所示的ERM问题以及下述的期望风险最小化问题:
$$ \begin{aligned} \min \ & \mathcal L(\boldsymbol{\theta})=\int_{\mathcal X\times \mathcal Y} L(f(\boldsymbol{x};\boldsymbol{\theta}),\boldsymbol{y})\text{d}\boldsymbol{P}(\boldsymbol{x},\boldsymbol{y}) \\ where:\ & \boldsymbol{\theta}\in\boldsymbol{\Theta} \end{aligned}\tag{3} $$
我们通常采用一种简化的表述。考虑一系列相互独立的、服从分布$\boldsymbol{P}$的随机变量序列:$\{ \boldsymbol{\xi}_{i}\}_{i=1}^N$,同时设$\boldsymbol{\xi}_{[i]}$为$\boldsymbol{\xi}$的若干可能值构成的集合,也即:$\boldsymbol{\xi}_{[i]}=(\boldsymbol{x}_i,\boldsymbol{y}_i)$或$\boldsymbol{\xi}_{[i]}=\{(\boldsymbol{x}_i,\boldsymbol{y}_i)\}_{i=1}^{N_i}$。记基于$\boldsymbol{\xi}_{[i]}$的误差为:$L_i(\boldsymbol{\theta})=L(\boldsymbol{\theta},\boldsymbol{\xi}_{[i]})$。从而我们的期望风险可以简化表述为:
$$ \mathcal L(\boldsymbol{\theta})=\mathbb{E}_{\boldsymbol{\xi}}[L(\boldsymbol{\theta},\boldsymbol{\xi})] $$
如果$\{\boldsymbol{\xi}_{[i]} \}_{i=1}^N$构成$\boldsymbol{T}$的一个分割,则经验风险可以表示为:
$$ \mathcal L(\boldsymbol{\theta};\boldsymbol{T})=\frac 1N \sum_{i=1}^N L_i(\boldsymbol{\theta},\boldsymbol{\xi}_{[i]}) $$
因此我们的任务可以写为:
$$ \begin{aligned} \min \ & \mathcal{L}(\boldsymbol{\theta};\boldsymbol{T})=\frac 1N \sum_{i=1}^N L_i(\boldsymbol{\theta},\boldsymbol{\xi}_{[i]}) \\ where:\ & \boldsymbol{\theta}\in\boldsymbol{\Theta} \end{aligned}\tag{4} $$
我们在之前的笔记中是用GD去求解ERM问题,它与求解期望风险最小化问题之间是有差距的,除了实践上的必然性之外,我们能否从理论上给出一个这么做的解释呢?
记问题(3)期望风险最小化问题的一个最优解为$\boldsymbol{\theta}^*_E$;问题(4)经验风险最小化问题的一个最优解为$\boldsymbol{\theta}^*$。同时记(4)迭代次数$\tau\geq1$后的解为$\boldsymbol{\theta}^{(\tau)}$,记:
$$ \epsilon(\tau)=\mathbb{E} [\mathcal L(\boldsymbol{\theta}^{(\tau)};\boldsymbol{T})-\mathcal L(\boldsymbol{\theta}^*;\boldsymbol{T}) ] $$
其中:$\mathbb{E}[\cdot]=\mathbb{E}_{\boldsymbol{\xi}_{i_{0}}}\cdots\mathbb{E}_{\boldsymbol{\xi}_{i_\tau-1}}[\cdot]$现在我们来考察:$\mathbb{E}[\mathcal L(\boldsymbol{\theta}^{(\tau)};\boldsymbol{T})-\mathcal L(\boldsymbol{\theta}^*_E)]$。根据参考资料1,我们有:
$$ \mathbb{E}[\mathcal L(\boldsymbol{\theta};\boldsymbol{T})-\mathcal L(\boldsymbol{\theta})]\leq O\left(\sqrt\frac{\log N}{N}\right) $$
注意到:
$$ \begin{align} \underbrace{\mathbb{E}[\mathcal L(\boldsymbol{\theta}^{(\tau)})-\mathcal L(\boldsymbol{\theta}^*_E)]}_{\mathcal E(N,\tau)}& =\underbrace{\mathbb E[\mathcal L(\boldsymbol{\theta}^{(\tau)})-\mathcal L(\boldsymbol{\theta}^{(\tau)};\boldsymbol{T})]}_{\leq O(\sqrt{(\log N)/N})} + \ \underbrace{\mathbb{E} [\mathcal L(\boldsymbol{\theta}^{(\tau)};\boldsymbol{T})-\mathcal L(\boldsymbol{\theta}^*;\boldsymbol{T}) ]}_{\epsilon(\tau)}\\ &+\underbrace{\mathbb{E} [\mathcal L(\boldsymbol{\theta}^*;\boldsymbol{T})-\mathcal L(\boldsymbol{\theta}_E^*;\boldsymbol{T}) ]}_{\leq 0}+\underbrace{\mathbb{E} [\mathcal L(\boldsymbol{\theta}^*_E;\boldsymbol{T})-\mathcal L(\boldsymbol{\theta}^*_E) ]}_{\leq O(\sqrt{(\log N)/N})} \end{align} $$
从而:
$$ \mathcal E(N,\tau)\leq O\left(2\sqrt{\frac {\log N}N}+\epsilon(\tau)\right) $$
由于在大规模机器学习特别是深度学习中,数据集的数量往往特别大,从而$\mathcal E(N,\tau)\propto \epsilon(\tau)$,从而我们在训练集上优化$\epsilon(\tau)$是合理的。
此外从另一方面,我们设数据维度为$d$,则优化算法达到$\epsilon$精度的运行时间为:
$$ \mathcal T(n,d,\epsilon)=nd\cdot \tau(\epsilon) $$
其中,$\tau(\epsilon)$是$\epsilon$-次优解集中所有解的迭代次数的最小值,具体地:
$$ \tau(\epsilon)=\underset{\tau}{\min}\{\epsilon(\tau)\leq \epsilon \} $$
显然确定了$\epsilon(\tau)$,$\tau(\epsilon)$与$\mathcal T(n,d,\epsilon)$也随之确定,这进一步从理论上说明了在数据集上确定$\epsilon(\tau)$变化规律对于求解期望风险最小化问题是合理的。鉴于这种合理性,因此在下文以及后续的所有笔记中,不再刻意区分$\mathcal L(\boldsymbol{\theta};\boldsymbol{T})$与$\mathcal L(\boldsymbol{\theta})$,统一记为后者。
从GD到SGD
那么说了这么多,我们应该如何改进Vanilla Gradient Descent呢?我们考虑以下参数更新公式:
$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta^{(\tau)} \cdot g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]}) \tag{5} $$
其中,$i_\tau$为随机从$\{1,\cdots,N \}$中选取的一个指标;$g$为实值函数,定义为:
$$ g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})= \begin{cases} \nabla L_i(\boldsymbol{\theta}^{(\tau)})=\nabla L(\boldsymbol{\theta}^{(\tau)};\boldsymbol{\xi}_{[i_\tau]}),&(SGD)\\ \frac{1}{N_{i_\tau}}\sum\limits_{j=1}^{N_{i_\tau}} \nabla L(\boldsymbol{\theta}^{(\tau)};\xi_{[i_\tau],j}),&(MSGD) \end{cases}\tag{6} $$
对于式(5)所示的优化算法,若$N_{i_\tau}\equiv 1$,即每个$\boldsymbol{\xi}_{[i_\tau]}$均为一个$\mathcal X\times \mathcal Y$的一个样本点,则称该算法为随机梯度下降算法(Stochastic gradient descent ,SGD)。若每个$\boldsymbol{\xi}_{[i_\tau]}$均为若干$\mathcal X\times \mathcal Y$的一个样本点的集合,则称该算法为小批量随机梯度下降算法(Mini-Batch SGD,MSGD)。
显然地,SGD本质上是用$g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})$来估计$\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)})$!由于指标$i_\tau$的选取是随机的,从而我们有:
$$ \mathbb{E}_{\boldsymbol{\xi}_{i_\tau}}[g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})]=\frac{1}{N}\sum_{i_\tau=1}^N g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})=\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)})\tag{7} $$
所以,$g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})$事实上是$\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)})$的一个无偏估计!类似地,对于MSGD也有相同结论。因此虽然$g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})$并不能保证都是目标函数的下降方向,但是在期望意义下,迭代序列$\{ \boldsymbol{\theta}^{(\tau)}\}$最终可以收敛到目标函数的一个极小值点 !从而证明了(5)式的有效性。
SGD、MSGD与GD的实践对比
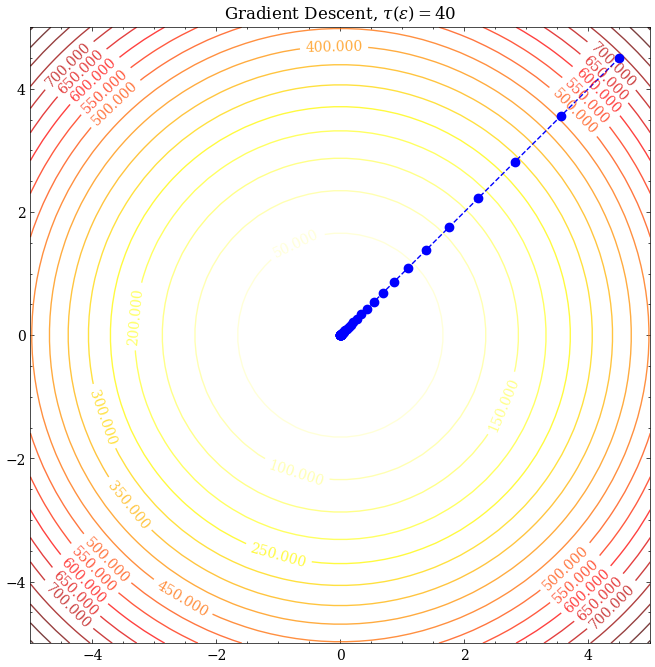
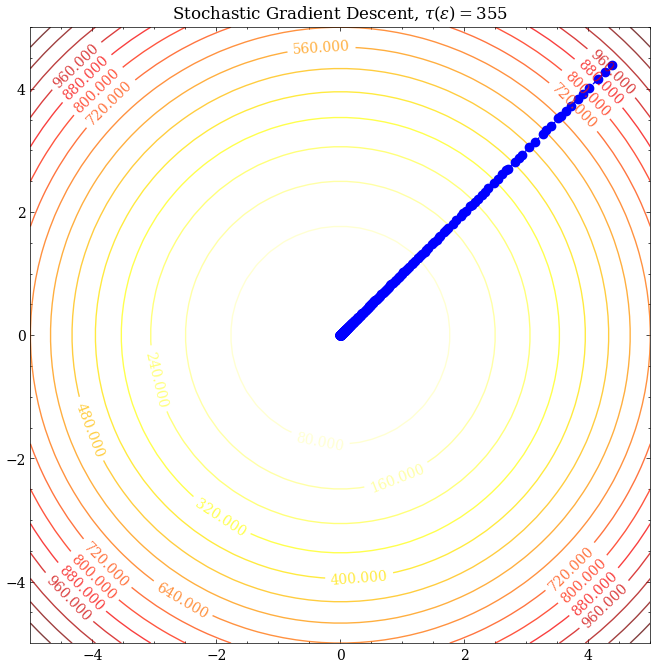
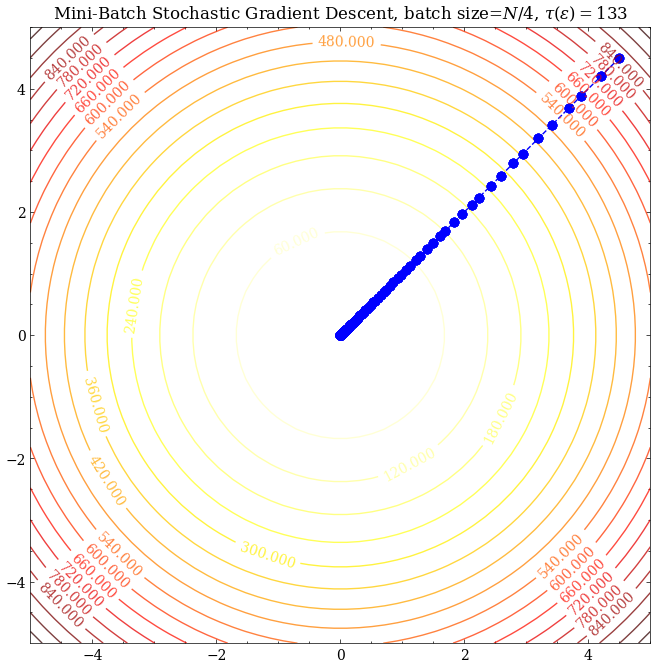
这里考虑目标函数为:
$$ \mathcal{L}(\theta_1,\theta_2)=\frac{1}{N}\sum_{i=1}^N x_i^2\cdot(\theta_1^2+\theta_2^2) $$
此时$\kappa=1$,可见三者都能很好地收敛至最优解。取$\epsilon=10^{-5}$,考察$\tau(\epsilon)$,可见SGD所需的迭代次数最多、MSGD其次、GD最少,猜想SGD的收敛速度应该比GD慢。那么有没有什么理论依据呢?我们接下来分析分析SGD的收敛速度。
References
- Estimation of Dependences Based on Empirical Data,Vladimir Vapnik
