前言
本章我们介绍几个凸优化算法。
系列文章
1、在介绍算法之前
本章我们讨论几种比较典型的优化算法。针对优化问题的类型,分为无约束问题与有约束问题两种情况进行分析。在优化领域中,所有的算法都是迭代算法,即形如:
$$ \boldsymbol{x}^{k+1}=\boldsymbol{x}^{k}+\alpha^k \boldsymbol{d}^k $$
其中$\boldsymbol{x}^k\in\boldsymbol{X}_f$为第$k$步时的解;$\boldsymbol{x}^{k+1}$为下一时刻的解;$\boldsymbol{d}^k$为前进方向,其维度与$\boldsymbol{x}$相同;$\alpha^k\in\mathbb{R},\alpha>0$为步长。
容易知道,在方向给定时,若目标函数为$f_0$是标量函数,则:
$$ \alpha^k = \underset{\alpha\geq 0}{\text{argmin}}f_0(\boldsymbol{x}^k+\alpha \boldsymbol{d}^k)\tag{1} $$
显然地,式(1)是一个关于$\alpha$的一维凸问题。这也被称为射线搜索问题。在实践中,求解$f_0(\boldsymbol{x}^k+\alpha \boldsymbol{d}^k)$关于$\alpha$的一阶偏导精确解出(1)的最优解往往是困难的,而事实上我们的重点是最小化$f_0(\boldsymbol{x})$,所以$\alpha$只需要让$f_0(\boldsymbol{x})$有足够小的减少即可。实践中我们往往采用下面两种方法,显然它们也是迭代算法:
(1)黄金分割法
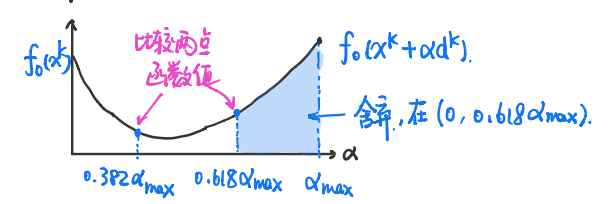
显然我们知道,$\alpha$往往有一个上界$\alpha_{max}$,我们在$(0,\alpha_{max}]$上取两点:$\alpha^1_1=0.618\alpha_{max}$与$\alpha_2^1=0.382\alpha_{max}$,比较$f_0(\boldsymbol{x}^k+\alpha _1^1\boldsymbol{d}^k)$与$f_0(\boldsymbol{x}^k+\alpha_2^1 \boldsymbol{d}^k)$的函数值,舍去较大的$\alpha^1$到端点的部分,而后再对剩下的区间进行上述迭代,图示:
(2)回溯直线法
设有两个参数:$\gamma\in(0,0.5],\beta\in(0,1)$,初始时设$\alpha=\alpha_{max}$,若:
$$ f_0(\boldsymbol{x}^k+\alpha \boldsymbol{d}^k)>f(\boldsymbol{x}^k)+\gamma \nabla_{\alpha} f_0(\boldsymbol{x}^k)^\top \boldsymbol{d}^k $$
则令$\alpha=\beta \alpha$,再进行迭代。
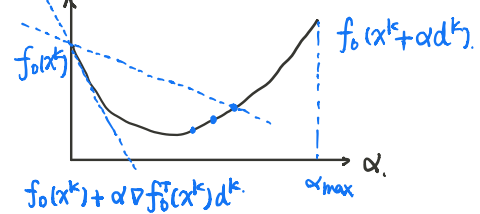
如上图所示,事实上我们需求的$\alpha$一定落在$(0,\alpha_0]$内,其中$\alpha_0$为$f_0(\boldsymbol{x}^k+\alpha \boldsymbol{d}^k)$与$f(\boldsymbol{x}^k)+\gamma \nabla_{\alpha} f_0(\boldsymbol{x}^k)^\top \boldsymbol{d}^k$交点的横坐标。
