神经网络基础

前言

  本文介绍了全连接神经网络的基本概念、结构、优化、以及一些其他问题。

1、从拟合问题说起

  我们考虑这样一个问题：设有一实值函数$f:\mathbb{R}^n\to\mathbb{R}^m$（下文称为目标函数），其形式未知，但函数$\boldsymbol{y}=f(\boldsymbol{x})$上有限个点构成的集合$\boldsymbol{T}=\{(\boldsymbol{x}_i,\boldsymbol{y}_i)\}_{i}^N$是已知的。如何在有限时间内利用有限的计算资源构造一个函数$f^*$（下文称为拟合函数），是某个度量函数间差异性的算子$\mathcal{L}$最小化？（或者直观地说得到一个最优近似）
  在实际中，函数拟合问题通常表现为回归或者曲线拟合的问题。很显然这是一个监督学习问题。就以回归问题为例，我们知道在经典的统计学习中，通常采用一个具有固定形式的基函数，而后基于最小二乘方法求解，例如线性回归最小二乘中有经典的解析解：$\boldsymbol{A}^\dagger\boldsymbol{Y}$，见最小二乘法-维基百科。
  根据泰勒展开式，一个很自然的想法便是基于高次多项式拟合。考虑到目标函数的任意性，我们期望多项式次数足够高，但是若目标函数是低次的多项式函数，便会带来极其严重的过拟合！此外，使用甚高次多项式函数进行拟合在计算效率上也是有严重问题的。
  因此在重重困难之下，我们需要一套新的理论与算法。核心问题便是：拟合函数应该基于数据具有自适应调整形式的能力！

2、仿射变换、激活函数与复合

  我们回过头来看多项式函数，真正制约它的是$\boldsymbol{x}^n$，但这恰恰是其在一些问题上获得成功的根本：非线性。我们如何在降低计算量的同时保留非线性呢？
  设$\boldsymbol{x}$是二维的，为了简化问题，我们假设使用二阶多项式函数逼近：$\frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Px}+\boldsymbol{q}^\top\boldsymbol{x}+r$，我们另设一二阶函数：$(\boldsymbol{a}^\top\boldsymbol{x}+b)^2$，编程实现这两者并比对50w次运行速度：

ans1= np.dot(x.T,P).dot(x)+np.dot(q.T,x)+r  # 2.52999
ans2 = (np.dot(a.T,x)+b)**2  # 1.44295

可以看出，后者的运行速度更快，事实上，我们做了两件事：

• 加权求和：广义而言是做了一个仿射变换；
• 逐点非线性运算：这里是逐点（也只有一个点）做了二次运算，也被称为激活函数

  所以，我们是将非线性变换从自变量身上（也即$\boldsymbol{x}^n$）转移到了其一个仿射变换的每一点上：$g(\boldsymbol{Wx}+\boldsymbol{b})$，其中$g$为逐点运算。这样，我们在保留非线性的同时显著降低了计算量。
  但是！这样做有一个问题，与多项式函数相比，表达能力是大大下降的。如何解决这个问题呢？直觉很快告诉我们：函数的复合！也即我们构造这样的一种形式：

$$ f^*(\boldsymbol{x})= f_2(g(f_1(\boldsymbol{x})))\tag{1} $$

其中：$f_1:\mathbb{R}^n\to\mathbb{R}^{d_1},f_2:\mathbb{R}^{d_1}\to\mathbb{R}^m$为仿射变换；$g:\mathbb{R}\to\mathbb{R}$为一维实值函数。为了防止平方后数值过大溢出，我们采用以下非线性更弱的函数：

$$ g(x)=\left\{\begin{aligned}1,&\,x\geq 0\\0,&\,x < 0\end{aligned}\right. $$

这个函数将负半轴强行归零，称为修正线性单元或线性整流单元，记为：$\text{ReLU}(x)$。所以，式（1）实际上是以下形式的函数：

$$ f^*(\boldsymbol{x})=\boldsymbol{W}_2\text{ReLU}(\boldsymbol{W}_1\boldsymbol{x}+\boldsymbol{b}_1)+\boldsymbol{b}_2\tag{2} $$

那么究竟这种复合能否解决我们在上文中提到的表达能力不足的问题呢？Cybenko与Hornik已经给出了答案：可以！事实上，对于$\mathbb{R}^n$上定义的任意Borel可测函数$f$，对于式（2）中定义的$f^*$有如下结论：

$$ |f(\boldsymbol{x})-f^*(\boldsymbol{x})|<\epsilon\tag{3} $$

其中$\epsilon$为一任意给定的正数。

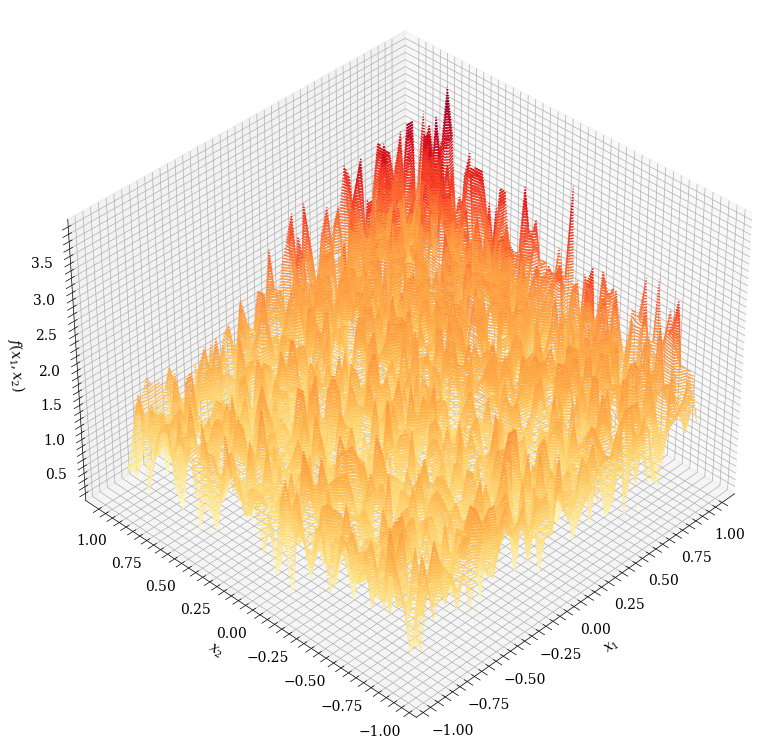
如果将$\text{ReLU}$看成一分段线性函数，是不是有点在实变函数中用分段线性函数逼近任意可测函数的意思呢？事实上如果我们随机取参数，$f^*$的图像如下：

确实有点像阶梯函数

  上述的定理也被称为人工神经网络的通用近似定理。等等，这不是一个复合函数吗？跟“神经网络”有什么关系？

3、神经元与神经网络

  为了看清楚式（2）我们引入如下的形式化记号：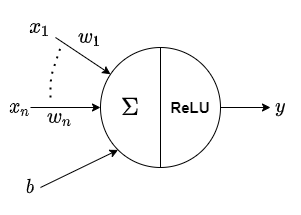

其被称为MP神经元，形如上图的神经元表达的是如下的函数：

$$ y=\sum_{i=1}^n w_ix_i +b $$

在不造成歧义的情况下，我们将圆圈中的算符省略，而将神经元的输出$y$写在圆圈中。所以，此时我们可以将仿射变换$f$与激活函数$g$放在一起用MP神经元表示，同时将变换前后的向量各个元素拆开，故而式（2）可以表示成如下的形式：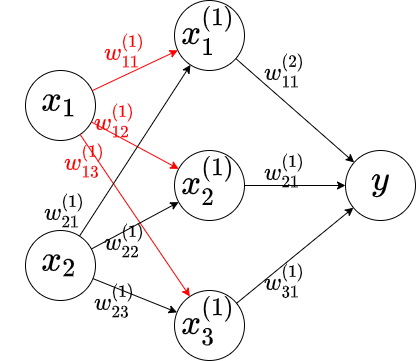

  正如上文所述，我们将 $g_i$与 $f_i$合到一起看成一组变换，某组变换与其对应的输入、输出构成的组合称为一层神经网络（one layer）。对于某层神经网络，称该层输出在激活函数前的向量为该层的状态（states），也即$output^{(i)}=g_i(states^{(i)})$。若某层神经网络的输入为整个模型的输入，则称其为输入层（input layer）；若某层神经网络的输出为整个模型的输出，则称其为输出层（output layer）；其余层均称为隐藏层（hidden layer）。从左至右，我们通常称各层为。同时在图示时我们常常略去加权因子、状态、偏差等，如下图所示：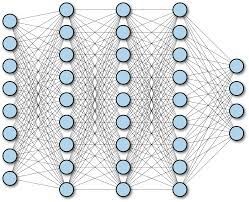
  从中我们可以看出此时模型具有网络状的结构，加之MP神经元是受到了生物神经元的启发，故而我们称形如式（3)的函数为神经网络。事实上，称式（3)为神经网络是一种狭义的表述，注意到上图中，前一层的状态正好是下一层的输入，层与层之间的连接是完全的，所以更为贴切的表述是全连接神经网络（Fully Connected Network，FCN)，其中的每一层被称为全连接层（FC layer，FC)。

4、神经网络的损失函数与梯度下降

  回到我们最开始的函数拟合问题，在第二部分中我们知道式（3）所示的函数可以任意精度逼近任意可测函数，但是如何去近似呢？
  设有数据集：$\boldsymbol{T}=\{(\boldsymbol{x}_i,\boldsymbol{y}_i)\}_{i}^N$，首先我们来刻画某个预测值$\boldsymbol{\hat y}$与其对应真实值$\boldsymbol{y}$之间的差异：

$$ L_{1}(\boldsymbol{\hat y},\boldsymbol{y})=||\boldsymbol{\hat y}-\boldsymbol{y}||_1=\sum_{i=1}^n |\hat y_i-y_i|\\\ or\ L_{2}(\boldsymbol{\hat y},\boldsymbol{y})=||\boldsymbol{\hat y}-\boldsymbol{y}||_2^2=\sum_{i=1}^n (\hat y_i-y_i)^2 $$

其中$y_i$代表向量$\boldsymbol{y}$的第$i$维取值。
  我们知道，神经网络的核心特点之一便是自适应性，其体现在层间加权因子上。设FCN总层数为$L$，则总体参数量为：

$$ P(f^*)=\sum_{l=1}^L d_ld_{l-1}+d_l $$

其中$d_l$表示第$l$层状态的维度。我们通常将所有参数记为$\boldsymbol{\theta}$，所有参数构成的集合称为参数空间，记为$\boldsymbol{\Theta}$，显然地，在我们这个问题中$\boldsymbol{\Theta}=\mathbb{R}^{P(f^*)}$。当参数取$\boldsymbol{\theta}_1\in\boldsymbol{\Theta}$时，数据集$\boldsymbol{T}$上有差异：

$$ \mathcal{L}_1(\boldsymbol{\theta}_1;\boldsymbol{T})=\sum_{i=1}^N L_1(\boldsymbol{\hat y}_i,\boldsymbol{y}_i)\\ \ or\ \mathcal{L}_2(\boldsymbol{\theta}_1;\boldsymbol{T})=\sum_{i=1}^N L_2(\boldsymbol{\hat y}_i,\boldsymbol{y}_i) $$

  我们通常将上式刻画的在$\boldsymbol{T}$上拟合值与真实值之间的差异称为经验风险，而将$L$称为损失函数。在机器学习领域中，我们通常称形如$L_1$的为MAE损失函数（MAE for Mean Absolute Error）；称形如$L_2$的为MSE损失函数（MSE for Mean Square Error）。此时，我们的函数拟合问题可以建模为：

$$ \min \mathcal{L}_{MAE}(\boldsymbol{\theta};\boldsymbol{T})\quad or \quad \min\mathcal{L}_{MSE}(\boldsymbol{\theta},\boldsymbol{T})\tag{*} $$

注意到此时$\boldsymbol{\theta}\in\mathbb{R}^{P(f^*)}$，所以这是一个无约束优化问题。我们文章在

中介绍了函数复合保凸的情况（定理2.2.4.2，定理2.2.4.3），对于ReLU函数，显然也是凸的，故而问题（）是一个凸问题！在无约束凸优化问题中，我们有经典的梯度下降方法（GD），由于$\mathcal{L}_{MAE}$不可微，所以我们采用MSE损失。将梯度下降算法应用于问题（）我们有参数更新公式：

$$ {\boldsymbol{\theta}^{(\tau)}=\boldsymbol{\theta}^{(\tau-1)}-\eta \cdot \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)} $$

其中，$\tau$为迭代次数（Step数），$\boldsymbol{\theta}^{(\tau)}$表示Step$=\tau$时的参数。特别地，$\boldsymbol{\theta}^{(0)}$称为初始参数，通常由某个预先设定的分布得来。$\eta>0$称为学习率，此处$\eta$刚好也是GD的步长。
  此外，在什么时候可以认为算法收敛了呢？我们称算法在Step$>m$后收敛，若以下三者中有其一满足：

• 设有一给定的阈值$l_0$，$\forall \tau_1,\tau_2>m,\tau_1\neq \tau_2,|\mathcal{L}\left(\boldsymbol{\theta}^{(\tau_1)} ; \boldsymbol{T}\right)-\mathcal{L}\left(\boldsymbol{\theta}^{(\tau_2)} ; \boldsymbol{T}\right)|<l$
• 设有一给定的阈值$\theta_0$，$\forall \tau_1,\tau_2>m,\tau_1\neq \tau_2,||\boldsymbol{\theta}^{(\tau_1)}-\boldsymbol{\theta}^{(\tau_2)}||_2<\theta_0$
• 设有一给定的阈值$\tau_0$，$m\geq \tau_0$

  所以，经典梯度下降算法为：

  我们知道，凸问题梯度下降算法是必然收敛于全局最优的，在这里就只简单进行一下可视化。由于对于高维函数可视化不好做，这里我们就相对固定其他参数，只研究$\boldsymbol{b}_1$，此时$\mathcal{L}$的图像为：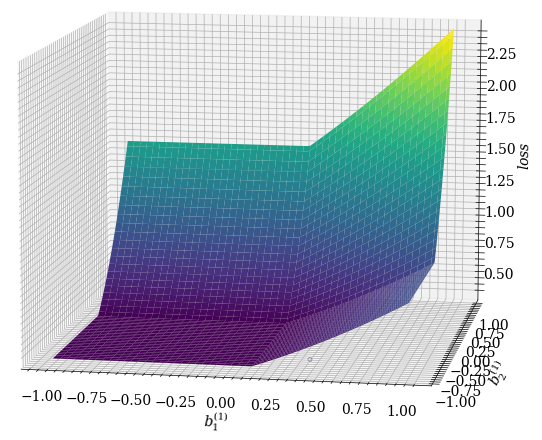

5、Backpropagation算法

  在上文的讨论中，我们介绍了模型的构建与优化算法，理论上已经足够完全了，但是我们在上文的分析中是将所有参数写在一起：$\boldsymbol{\theta}$，假设我们一共有$L$层，第$l$层状态的维度为$d_l$，输入的维度为$n$，则我们要求解的是：

$$ \nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)=\begin{bmatrix} \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial\theta^{(\tau-1)}_1}\\ \vdots\\ \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial\theta^{(\tau-1)}_{d_L}} \end{bmatrix}_{d_L\times 1} $$

而事实上各个参数之间是有联系的，如果直接求解上式会极其复杂，有没有什么好办法呢？我们来分析一下。值得注意的是，本节需要用到很多矩阵微分与求导的知识，详细内容参见：

  设第$l(1\leq l< L)$层的输入为$\boldsymbol{x}^{(l-1)}\in\mathbb{R}^{d_{l-1}\times 1}$，该层仿射变换权重与偏差分别为$\boldsymbol{W}^{(l)}\in\mathbb{R}^{d_{l}\times d_{l-1}},\boldsymbol{b}^{(l)}\in\mathbb{R}^{d_l\times 1}$，则记该层的状态为：

$$ \boldsymbol{h}^{(l)}=\boldsymbol{W}^{(l)}\boldsymbol{x}^{(l-1)}+\boldsymbol{b}^{(l)}=\begin{bmatrix} h^{(l)}_1\\ \vdots\\ h^{(l)}_{d_l} \end{bmatrix}_{d_{l}\times 1} =\begin{bmatrix} b_1^{(l)}+\sum\limits_{i=1}^{d_{l-1}} w_{1i}x_i\\ \vdots\\ b_{d_l}^{(l)}+\sum\limits_{i=1}^{d_{l-1}} w_{d_li}x_i\\ \end{bmatrix}\tag{4} $$

我们现在来考察$\frac{\partial \boldsymbol{h}^{(l)}}{\partial \boldsymbol{W}^{(l)}}$与$\frac{\partial \boldsymbol{h}^{(l)}}{\partial \boldsymbol{b}^{(l)}}$，由（4）式我们有：

$$ \begin{align} \frac{\partial \boldsymbol{h}^{(l)}}{\partial \boldsymbol{b}^{(l)}}&=[\frac{\partial h_i^{(l)}}{\partial b_j^{(l)}}]_{d_l\times d_l}\\ &=\boldsymbol{I}_{d_l} \end{align}\tag{5} $$

同时：

$$ \begin{align} \frac{\partial \boldsymbol{h}^{(l)}}{\partial \boldsymbol{W}^{(l)}}&=[\frac{\partial h_i^{(l)}}{\partial \text{vec}(\boldsymbol{W})}]_{d_l\times (d_l\cdot d_{l-1})}\\ &=\begin{bmatrix} \frac{\partial h_1^{(l)}}{\partial w_{11}^{(l)}} & \cdots&\frac{\partial h_1^{(l)}}{\partial w_{d_l1}^{(l)}}&\cdots&\frac{\partial h_1^{(l)}}{\partial w_{1d_{l-1}}^{(l)}} & \cdots&\frac{\partial h_1^{(l)}}{\partial w_{d_ld_{l-1}}^{(l)}}\\ \vdots & \ddots &\vdots & \ddots &\vdots & \ddots &\vdots\\ \frac{\partial h_{d_l}^{(l)}}{\partial w_{11}^{(l)}} & \cdots&\frac{\partial h_{d_l}^{(l)}}{\partial w_{d_l1}^{(l)}}&\cdots&\frac{\partial h_{d_l}^{(l)}}{\partial w_{1d_{l-1}}^{(l)}} & \cdots&\frac{\partial h_{d_l}^{(l)}}{\partial w_{d_ld_{l-1}}^{(l)}}\\ \end{bmatrix}_{d_l\times (d_l\cdot d_{l-1})}\\ &=\begin{bmatrix}\underbrace{ \text{diag}\{\overbrace{x_1^{(l-1)},\cdots,x_1^{(l-1)}}^{d_l个}\},\cdots, \text{diag}\{\overbrace{x_{d_{l-1}}^{(l-1)},\cdots,x_{d_{l-1}}^{(l-1)}}^{d_l个}\}}_{d_{l-1}个对角矩阵} \end{bmatrix}_{d_l\times (d_l\cdot d_{l-1})} \end{align}\tag{6} $$

  同时，我们记损失对第$l$层状态的偏导为：

$$ \boldsymbol{\delta}^{(l)}=\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{h}^{(l)}}=\begin{bmatrix} \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial h_1^{(l)}}\\ \vdots\\ \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial h_{d_l}^{(l)}} \end{bmatrix}_{d_l\times 1} =\begin{bmatrix} \delta_1^{(l)}\\ \vdots\\ \delta_{d_l}^{(l)}\\ \end{bmatrix} \tag{7} $$

  现在回到我们的正题上来，我们在上文中分析到直接求解$\nabla_{\boldsymbol{\theta}} \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)$对参数进行整体更新不好做，那如果已知损失对第$l$层状态的偏导$\boldsymbol{\delta}^{(l)}$呢？由一元导数的链式求导法则：

$$ \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial}=\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial h_i^{(l)}}\cdot \frac{\partial h_i^{(l)}}{\partial} $$

则立刻有：

$$ \begin{align} \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{b}^{(l)}}&=\boldsymbol{\delta}^{(l)}\\ \text{unvec}\left(\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{W}^{(l)}}\right)&=\boldsymbol{\delta}^{(l)}\cdot \left(\boldsymbol{x}^{(l-1)}\right)^\top\tag{8} \end{align} $$

所以如果我们已知$\boldsymbol{\delta}^{(l)}$，那么根据（8）式可以很轻易地对$\boldsymbol{W}^{(l)},\boldsymbol{b}^{(l)}$进行更新。所以现在的核心问题转化为了求解$\boldsymbol{\delta}^{(l)}$。
  对于$1\leq l \leq L-2$的中间的隐藏层，我们知道：

$$ \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{h}^{(l)}}=\left(\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial (\boldsymbol{h}^{(l+1)})^\top}\cdot\frac{\partial \boldsymbol{h}^{(l+1)}}{\partial \boldsymbol{h}^{(l)}}\right)^\top\tag{9} $$

  如果第$l$层的激活函数为$g^{(l)}:\mathbb{R}\to\mathbb{R}$，由于它是逐点的，则该层输出也即第$l+1$层的输入为：

$$ \boldsymbol{x}^{(l)}=g^{(l)}(\boldsymbol{h}^{(l)})=\begin{bmatrix} g^{(l)}(h_1^{(l)})\\ \vdots\\ g^{(l)}(h_{d_l}^{(l)}) \end{bmatrix}_{d_l\times 1}\tag{10} $$

  所以由（10）式：

$$ \frac{\partial \boldsymbol{x}^{(l)}}{\partial \boldsymbol{h}^{(l)}}=\begin{bmatrix} \frac{\partial g^{(l)}(h_1^{(l)})\\}{\partial h_1^{(l)}} & \cdots & \frac{\partial g^{(l)}(h_1^{(l)})\\}{\partial h_{d_l}^{(l)}}\\ \vdots & \ddots & \vdots\\ \frac{\partial g^{(l)}(h_{d_l}^{(l)})\\}{\partial h_{d_l}^{(l)}} & \cdots & \frac{\partial g^{(l)}(h_{d_l}^{(l)})\\}{\partial h_{d_l}^{(l)}}\\ \end{bmatrix}_{d_l\times d_l}=\text{diag}\{\frac{\partial g^{(l)}(h_1^{(l)})\\}{\partial h_1^{(l)}},\cdots,\frac{\partial g^{(l)}(h_{d_l}^{(l)})\\}{\partial h_{d_l}^{(l)}}\}\tag{11} $$

为了下文表示方便，我们记向量：

$$ g'^{(l)}(\boldsymbol{h}^{(l)})=\begin{bmatrix} \frac{\partial g^{(l)}(h_1^{(l)})\\}{\partial h_1^{(l)}}\\ \vdots\\ \frac{\partial g^{(l)}(h_{d_l}^{(l)})\\}{\partial h_{d_l}^{(l)}} \end{bmatrix}_{d_l\times 1}\tag{12} $$

  此外：

$$ \boldsymbol{h}^{(l+1)}=\boldsymbol{W}^{(l+1)}g^{(l)}(\boldsymbol{h}^{(l)})+b^{(l+1)}\tag{13} $$

所以有：

$$ \frac{\partial \boldsymbol{h}^{(l+1)}}{\partial \boldsymbol{h}^{(l)}}=\begin{bmatrix} w_{11}^{(l+1)}\frac{\partial g^{(l)}(h_1^{(l)})\\}{\partial h_1^{(l)}}&\cdots &w_{1d_l}^{(l+1)}\frac{\partial g^{(l)}(h_{d_l}^{(l)})\\}{\partial h_{d_l}^{(l)}}\\ \vdots&\ddots &\vdots\\ w_{d_{l+1}1}^{(l+1)}\frac{\partial g^{(l)}(h_1^{(l)})\\}{\partial h_1^{(l)}}&\cdots &w_{d_{l+1}d_l}^{(l+1)}\frac{\partial g^{(l)}(h_{d_l}^{(l)})\\}{\partial h_{d_l}^{(l)}} \end{bmatrix}_{d_{l+1}\times d_l} $$

将上式代入（9），并结合（12）可知

$$ \boldsymbol{\delta}^{(l)}=\left(\left(\boldsymbol{W}^{(l+1)}\right)^\top\boldsymbol{\delta}^{(l+1)}\right)\odot g'^{(l)}(\boldsymbol{h}^{(l)})\tag{14} $$

其中$\odot$为Hadamard积。特别地，对于输入层：

$$ \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{x}}=\left(\boldsymbol{W}^{(1)}\right)^\top\boldsymbol{\delta}^{(1)}\tag{16} $$

  此外对于$\boldsymbol{\delta}^{(L-1)}$，我们将（3）中输出层的仿射变换进一步推广成：

$$ \boldsymbol{y}=f_{output}(\boldsymbol{x}^{(L)})=f_{output}(g^{(L-1)}(\boldsymbol{h}^{(L-1)})) \in\mathbb{R}^{d_L\times 1} $$

则有：

$$ \begin{align} \boldsymbol{\delta}^{(L-1)}&=\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{h}^{(L-1)}}\\ &=\left(\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{y}^\top}\cdot \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}^{(L)}}\right)^\top\cdot g'^{(L-1)}(\boldsymbol{h}^{(L-1)})\\ &=\left(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}^{(L)}}\right)^\top\cdot \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{y}}\cdot g'^{(L-1)}(\boldsymbol{h}^{(L-1)})\\ \end{align}\tag{17} $$

  所以，综合（8）（9）（13）（14）（17）式，我们完整的梯度下降算法计算式。为了看清楚我们将迭代轮次放在符号右下角，于是有：

$$ \begin{equation} \left\{ \begin{aligned} &\boldsymbol{\delta}^{(L-1)}=\left(\frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}^{(L)}}\right)^\top\cdot \frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{y}}\cdot g'^{(L-1)}(\boldsymbol{h}^{(L-1)})\\ &\frac{\partial \mathcal{L}\left(\boldsymbol{\theta}^{(\tau-1)} ; \boldsymbol{T}\right)}{\partial \boldsymbol{x}}=\left(\boldsymbol{W}_{(\tau-1)}^{(1)}\right)^\top\boldsymbol{\delta}_{(\tau-1)}^{(1)}\\ &\boldsymbol{\delta}_{(\tau-1)}^{(l)}=\left(\left(\boldsymbol{W}_{(\tau-1)}^{(l+1)}\right)^\top\boldsymbol{\delta}_{(\tau-1)}^{(l+1)}\right)\odot g'^{(l)}(\boldsymbol{h}_{(\tau-1)}^{(l)}),\ 1\leq l <L-1\\ &\boldsymbol{W}_{(\tau)}^{(l)}=\boldsymbol{W}_{(\tau-1)}^{(l)}-\eta\cdot \boldsymbol{\delta}_{(\tau-1)}^{(l)}\cdot \left(\boldsymbol{x}_{(\tau-1)}^{(l-1)}\right)^\top\\ &\boldsymbol{b}_{(\tau)}^{(l)}=\boldsymbol{b}_{(\tau-1)}^{(l)}-\eta\cdot \boldsymbol{\delta}^{(l)}_{(\tau-1)} \end{aligned} \right. \end{equation}\tag{17} $$

  从上式可以看出，梯度更新是从最后一层逐渐向第一次推进的，故而也被称为反向传播（Backpropagation）算法。

6、实践

  接下来我们编程实践一下。我们还是考虑我们的函数拟合问题，目标函数为：

$$ f(x_1,x_2)=x_1+x_2 $$

在第二部分我们介绍了通用近似定理，我们取我们的FCN模型为：

$$ f^*(x_1, x_2)=\boldsymbol{W}_2\text{ReLU}(\boldsymbol{W}_1\boldsymbol{x}+\boldsymbol{b}_1)+b_2\tag{19} $$

  其中：$\boldsymbol{W}_1\in\mathbb{R}^{2\times hidden\ dim},\boldsymbol{W}_2\in\mathbb{R}^{hidden\ dim\times 1},\boldsymbol{b}_1\in\mathbb{R}^{hidden\ dim\times 1},b\in\mathbb{R}$，我们取隐藏层维度为100（事实上这是一个两层的网络，严格而言只有输入层与输出层，没有隐藏层的说法，称为中间维度更严谨）。所以，如果我们将激活函数与仿射变换解耦，则我们只需设计两个类：FullyConnectedLayer（也叫线性层）和ReLU。
  对于这两个类，需要完成的功能有：前向计算本层的输出（forward）、反向计算本层参数的梯度（backward）、更新参数等，我们设计一个基类：

class BaseNetwork:
    def __init__(self):
        pass
    def forward(self, *x):
        pass
    def parameters(self):
        pass
    def backward(self, grad):
        pass
    def __call__(self, *x):
        return self.forward(*x)

我们采用PyTorch风格，将参数的更新放到优化器类中。
  对于Linear层，完成的变换为：

$$ \boldsymbol{H}=\boldsymbol{W}\cdot \boldsymbol{X}+\boldsymbol{b} $$

若从上层传下来的梯度为$\frac{\partial \mathcal{L}}{\partial \boldsymbol{H}_{(\tau-1)}}$，则由（17）式立刻有：

$$ \begin{equation} \left\{ \begin{aligned} &\frac{\partial \mathcal{L}}{\partial \boldsymbol{W}_{(\tau-1)}}= \frac{\partial \mathcal{L}}{\partial \boldsymbol{H}_{(\tau-1)}}\boldsymbol{X}_{(\tau-1)}^\top\\ &\frac{\partial \mathcal{L}}{\partial \boldsymbol{b}_{(\tau-1)}}=\frac{\partial \mathcal{L}}{\partial \boldsymbol{H}_{(\tau-1)}}\\ &\frac{\partial \mathcal{L}}{\partial \boldsymbol{X}_{(\tau-1)}}=\boldsymbol{W}_{(\tau-1)}^\top\frac{\partial \mathcal{L}}{\partial \boldsymbol{H}_{(\tau-1)}} \end{aligned} \right. \end{equation}\tag{20} $$

所以线性层的代码为：

class Linear(BaseNetwork):
    def __init__(self, input_dim, output_dim, std=0.1):
        super(Linear, self).__init__()
        self.weight = np.random.normal(loc=0.0, scale=std, size=(output_dim, input_dim))
        self.bias = np.random.normal(loc=0.0, scale=std, size=[output_dim, 1])
        self.input, self.output = None, None
        self.wgrad, self.bgrad = np.zeros(self.weight.shape), np.zeros(self.bias.shape)
        self.variable = Variable(self.weight, self.wgrad, self.bias, self.bgrad)
    
    def parameters(self):
        return self.variable
    
    def forward(self, *x):
        x = x[0]
        self.input = x
        self.output = np.dot(self.weight, self.input) + self.bias
        return self.output
    
    def backward(self, grad):
        self.bgrad = grad
        self.wgrad += np.dot(grad, self.input.T)
        grad = np.dot(self.weight.T, grad)
        return grad

  ReLU层就很简单啦：

class Relu(BaseNetwork):
    def __init__(self):
        super(Relu, self).__init__()
        self.input, self.output = None, None
    
    def forward(self, *x):
        x = x[0]
        self.input = x
        x[self.input <= 0] *= 0
        self.output = x
        return self.output
    
    def backward(self, grad):
        grad[self.input > 0] *= 1
        grad[self.input <= 0] *= 0
        return grad

  而我们的优化器需要完成的功能是梯度的清除与参数的更新：

class Vanilla_GD:
    def __init__(self, parameters, lr=1e-2):
        self.parameters = parameters
        self.lr = lr
    
    def zero_grad(self):
        for parameters in self.parameters:
            parameters.wgrad *= 0
            parameters.bgrad *= 0
    
    def step(self):
        for parameters in self.parameters:
            parameters.weight += parameters.v_weight  - self.lr * parameters.wgrad
            parameters.bias -= self.lr * parameters.bgrad

  模型的主题代码就介绍完了，最后介绍损失函数。为了求导方便，我们取：

$$ \mathcal{L}\left(\boldsymbol{\theta} ; \boldsymbol{T}\right)=\frac{1}{2N}\sum_{i=1}^ N ||\boldsymbol{\hat y}_i-\boldsymbol{y}_i||_2^2 $$

我们在第五部分中得出的参数更新公式为输入为单个样本的情况，而经典GD要求我们计算整体训练集上的梯度，我们可以适当修改公式，或者直接手动地累计梯度再除以$N$。
  我们画出训练过程中的Loss曲线图：

红色线为训练集误差，蓝色线为测试集误差，我们可以认为算法在$\tau>6$后收敛。函数图如下：

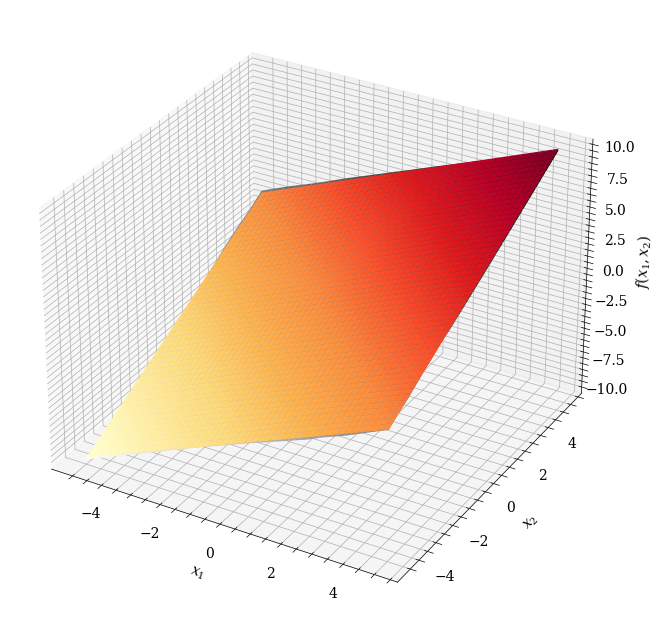
其中黑白的为拟合函数的曲面，而彩色的为目标函数曲面，二者已经相当接近了。

7、小结

  至此，FCN的所有内容就介绍完了，虽然从现代深度学习的视角来看FCN极其简陋，甚至不应该被称为深度学习模型，但是它确实是深度学习的起源之一，关于上述的函数拟合任务可以衍生出很多值得深挖的问题，就这个意义上来说，FCN的意义不可不谓重大。