前言
本文介绍凸函数、强凸函数与L-光滑函数的性质。
我们在文章:
中介绍了凸函数:设有函数$f:\mathbb{R}^n\to\mathbb{R}$,若:
- 定义域是凸集:$\text{dom}f$是凸集
- 凸组合的函数值$\leq$函数值的凸组合:
$$ f(\theta\boldsymbol{x}+(1-\theta)\boldsymbol{y})\leq\theta f(\boldsymbol{x})+(1-\theta)\boldsymbol{y},0\leq\theta \leq1,\tag{1} $$
则称$f$是凸函数。若等号处处不成立,则称$f$是严格凸的。凸函数有哪些性质呢?
Jensen不等式
定理1:Jensen不等式
由凸函数的定义,显然我们可以拓展至更多点的凸组合:设有凸函数$f$,$\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n\in\text{dom} f$,$\theta_1,\cdots,\theta_n \geq0,\sum_{i=1}^n \theta_i=1$,则:
$$ Jensen:\quad f\left(\sum_{i=1}^n\theta_i \boldsymbol{x}_i\right)\leq \sum_{i=1}^n \theta_i \boldsymbol{x}_i\tag{1} $$
同时我们也可以推广至其他领域,例如积分形式的Jensen不等式。若在$\boldsymbol{S}\subseteq \text{dom}f$上有$p(\boldsymbol{x})\geq 0$且$\int_\boldsymbol{S} p(\boldsymbol{x})\text d \boldsymbol{x}=1$,则:
$$ f\left(\int_{\boldsymbol{S}} \boldsymbol{x}p(\boldsymbol{x})\text d \boldsymbol{x}\right)\leq \int_\boldsymbol{S}f(\boldsymbol{x})p(\boldsymbol{x})\text d \boldsymbol{x}\tag{2} $$
若$p(\boldsymbol{x})$是随机变量$X$的概率函数,则还有期望形式的Jensen不等式:
$$ f\left(\mathbb{E}[X]\right)\leq\mathbb{E}[f(X)]\tag{3} $$
当然使用最为广泛的形式莫过于:
$$ f\left(\frac{\boldsymbol{x}+\boldsymbol{y}}{2}\right)\leq \frac{f(\boldsymbol{x})+f(\boldsymbol{y})}{2}\tag{4} $$
Jensen不等式与其他不等式的联系
对于Jensen不等式,我们选取合适的$f$再经过变换可以得到很多著名的不等式,如对式(1),取$\theta_i\equiv \frac{1}{n},f(x)=\log x$,由$f$为凹函数,则:
$$ \log \left(\sum_{i=1}^n \frac{x_i}{n}\right)\geq \sum_{i=1}^n \frac{\log x_i}{n} $$
再在两边取指数,从而有AM-GM不等式:
定理2:AM-GM不等式
$$ AM-GM:\quad \frac{\sum\limits_{i=1}^n x_i}{n}\geq \left(\prod_{i=1}^n x_i\right)^\frac{1}{n}\tag{5} $$
又如Hölder不等式:
定理3:Hölder不等式
$$ H\ddot{o}lder:\quad ||\boldsymbol{xy}||_1=||\boldsymbol{x}||_p\cdot||\boldsymbol{y}||_q,\ p^{-1}+q^{-1}=1,p> 1\tag{6} $$
具体地:
$$ H\ddot{o}lder:\quad \sum _{{i=1}}^{n}|x_{i}y_{i}|\leq \left(\sum _{{i=1}}^{n}|x_{i}|^{p}\right)^{{1/p}}\left(\sum _{{i=1}}^{n}|y_{i}|^{q}\right)^{{1/q}},\ p^{-1}+q^{-1}=1,p> 1\tag{7} $$
更多的情况就不再赘述了。
Hölder不等式同样有积分形式:
$$ |\int_a^bf(x)g(x) \mathrm d x| \le (\int_a^b |f(x)|^p \mathrm d x)^{\frac{1}{p}}(\int_a^b |g(x)|^q \mathrm d x)^{\frac{1}{q}},\ p^{-1}+q^{-1}=1,p> 1\tag{8} $$
而且在积分收敛的情况下可以推广至无穷积分。
强凸性
设有函数$f:\mathbb{R}^n\to\mathbb{R}$,且$f$二阶可微,其在$\boldsymbol{x}$处的一阶导数为$\nabla f(\boldsymbol{x})$,二阶导数即Hessian矩阵为$\nabla^2 f(\boldsymbol{x})$,在不引起歧义的情况下我们将其简记为$\boldsymbol{H}$。下文的范数$\|\cdot \|$均为标准内积诱导的2范数。这些前置条件下文不再赘述。
定义1:函数的强凸性
若$\forall \boldsymbol{x}$,有$\boldsymbol{H}\succeq \mu \boldsymbol{I}$,其中$\mu>0$,$\boldsymbol{I}$为$n$阶单位阵,也即$\boldsymbol{H}-\mu\boldsymbol{I}\succeq 0$,则称$f$是$\mu$-强凸的。显然这为$\boldsymbol{H}$的最小特征值规定了一个下界。
定理4:强凸性的等价表述
以下表述等价:
(A)$f$是$\mu$-强凸的,即$\boldsymbol{H}\succeq \mu\boldsymbol{I}$;
(B)$f(\boldsymbol{y}) \geq f(\boldsymbol{x}) + \left\langle \nabla f(\boldsymbol{x}),\ \boldsymbol{y}-\boldsymbol{x} \right\rangle + \frac \mu2 \| \boldsymbol{y}-\boldsymbol{x} \|^2$
(C)$\left\langle \nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x}),\ \boldsymbol{y}-\boldsymbol{x} \right\rangle \geq \mu \| \boldsymbol{y}-\boldsymbol{x} \|^2 $,或者$\left\| \nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x}) \right\| \geq \mu\|\boldsymbol{y}-\boldsymbol{x} \|$
(D)$\alpha f(\boldsymbol{x}) + (1-\alpha)f(\boldsymbol{y}) - f\left( \alpha \boldsymbol{x} + (1-\alpha)\boldsymbol{y} \right) \geq \frac{\alpha(1-\alpha)\mu}{2} \| \boldsymbol{y}-\boldsymbol{x} \|^2 ,\alpha\in[0,1]$
其中,(C)被称为强连续性。显然地,若$\mu=0$,则上式退化成凸函数的等价定义,这便是强字的由来。
证明:
我们先来证(A)与(B)等价。我们在:
中介绍了多元函数的Taylor公式,所以:
$$ f(\boldsymbol{y}) = f(\boldsymbol{x}) + \left\langle \nabla f(\boldsymbol{x}),\boldsymbol{y}-\boldsymbol{x} \right\rangle + \frac12\left\langle \nabla^2 f(\boldsymbol{\xi}) (\boldsymbol{y}-\boldsymbol{x}),\boldsymbol{y}-\boldsymbol{x} \right\rangle\tag{7} $$
其中$\boldsymbol{\xi}=\boldsymbol{x}+\theta\boldsymbol{y},\theta\in(0,1)$。若$\boldsymbol{H}\succeq \mu\boldsymbol{I}$,则$(\boldsymbol{y}-\boldsymbol{x})^\top(\boldsymbol{H}-\mu\boldsymbol{I})(\boldsymbol{y}-\boldsymbol{x})\geq 0$,从而(B)易证。同时若(2)满足,则有$\boldsymbol{H}[f(\boldsymbol{\xi})]\succeq \mu\boldsymbol{I}$,由于$\boldsymbol{x},\boldsymbol{y}$是任取的,则有(A)成立。
(B)$\Rightarrow$(C):
由(B)知:
$$ \begin{align} f(\boldsymbol{y}) &\geq f(\boldsymbol{x}) + \left\langle \nabla f(\boldsymbol{x}),\ \boldsymbol{y}-\boldsymbol{x} \right\rangle + \frac \mu2 \| \boldsymbol{y}-\boldsymbol{x} \|^2\\ f(\boldsymbol{x}) &\geq f(\boldsymbol{y}) + \left\langle \nabla f(\boldsymbol{y}),\ \boldsymbol{x}-\boldsymbol{y} \right\rangle + \frac \mu2 \| \boldsymbol{x}-\boldsymbol{y} \|^2 \end{align} $$
两式相加即得(C)。
(C)$\Rightarrow$(B):
考虑函数
$$ g(t)=f(\boldsymbol{x}+t(\boldsymbol{y}-\boldsymbol{x}))-\frac{\mu t^2}{2}||\boldsymbol{y}-\boldsymbol{x}||^2\tag{8} $$
则:
$$ g'(t)=\nabla f(\boldsymbol{x}+t(\boldsymbol{y}-\boldsymbol{x}))^\top (\boldsymbol{y}-\boldsymbol{x})+\mu t||\boldsymbol{y}-\boldsymbol{x}||^2 $$
记$\boldsymbol{p}_i=\boldsymbol{x}+t_i(\boldsymbol{y}-\boldsymbol{x})$,则:
$$ \begin{align} \left(g^{\prime}\left(t_{1}\right)-g^{\prime}\left(t_{2}\right)\right)\left(t_{1}-t_{2}\right) &=\left(\nabla f\left(\boldsymbol{p}_{1}\right)-\nabla f\left(\boldsymbol{p}_{2}\right)\right)^\top\left(\boldsymbol{p}_{1}-\boldsymbol{p}_{2}\right) -\mu\left\|\boldsymbol{p}_{1}-\boldsymbol{p}_{2}\right\|^2\\ \end{align} $$
由(C)结合上式可知$g'(t)$是增函数,所以$g(t)$关于$t$是一个凸函数!同时我们又知道,$g(1)=f(\boldsymbol{y})-\frac{\mu}{2} ||\boldsymbol{y}-\boldsymbol{x}||^2$,$g(0)=f(\boldsymbol{x})$,$g'(0)=\nabla f(\boldsymbol{x})^\top (\boldsymbol{y}-\boldsymbol{x})$,我们要证明的(B)即为:
$$ g(1)\geq g(0)+g'(0)\tag{9} $$
由$g(t)$是凸函数,结合凸优化二:凸函数中的定义2.1.1.3可证。
至此,我们已经证明了(A)(B)(C)等价,最后我们来看(D)。若(C)成立,则在上一部分证明(C)$\Rightarrow$(B)时,我们证明了(8)式的函数:
$$ g(t)=f(\boldsymbol{x}+t(\boldsymbol{y}-\boldsymbol{x}))-\frac{\mu t^2}{2}||\boldsymbol{y}-\boldsymbol{x}||^2 $$
是一个凸函数,则对于任意$\alpha\in[0,1]$,有:
$$ \alpha g(t_1)+(1-\alpha)g(t_2)\geq g(\alpha t_1+(1-\alpha)t_2)\tag{10} $$
取$t_1=0,t_2=1$,代入上式即可得(D)成立。若(D)成立,则结合函数$g(t)$有:
$$ \alpha g(0)+(1-\alpha)g(1)\geq g(1-\alpha) $$
记函数$h(\alpha)=\alpha g(0)+(1-\alpha)g(1)-g(1-\alpha),\alpha\in[0,1]$,由$h(0)=h(1)=0$,且$h\geq 0$,在1的一个左邻域$[1-\delta,1]$内,要么$h\equiv 0$,此时$h'(1)=0$;要么$h>0$,此时$h'(1)<0$。总而言之,1处$h$的导数$h'(1)=g(0)-g(1)+g'(0)\leq 0$,从而式(9)成立,从而(B)成立,从而定理4得证。
Lipschitz光滑
定义2:Lipschitz光滑性
若$\exists L>0$使得$\forall \boldsymbol{x},\boldsymbol{y}$有:
$$ \|\nabla f(\boldsymbol{y})-\nabla f(\boldsymbol{x}) \|\leq L\|\boldsymbol{y}-\boldsymbol{x} \| $$
即$f$的一阶导函数是Lipschitz连续的,则称$f$是Lipschitz光滑的,Lipschitz常数为$L$,简称为$L$-光滑的。
定理5:凸函数的$L$-光滑等价表述
设$f$是凸函数,则以下表述等价:
(a)$f$是$L$-光滑的,即$\|\nabla f(\boldsymbol{y})-\nabla f(\boldsymbol{x}) \|\leq L\|\boldsymbol{y}-\boldsymbol{x} \|$
(b)$0 \leq f(\boldsymbol{y})-f(\boldsymbol{x}) - \left\langle \nabla f(\boldsymbol{x}),\ \boldsymbol{y}-\boldsymbol{x} \right\rangle \leq \frac L2 \left\| \boldsymbol{y}-\boldsymbol{x} \right\|^2 $
(c)$\frac{1}{L}||\nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x})||^2\leq \left\langle \nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x}),\ \boldsymbol{y}-\boldsymbol{x} \right\rangle \leq L \left\|\boldsymbol{y}-\boldsymbol{x} \right\|^2$
(d)$0\leq \alpha f(\boldsymbol{x}) + (1-\alpha)f(\boldsymbol{y}) - f\left( \alpha \boldsymbol{x} + (1-\alpha)\boldsymbol{y} \right) \leq \frac{\alpha(1-\alpha)L}2 \| \boldsymbol{y}-\boldsymbol{x} \|^2$
(e)$\boldsymbol{H}\preceq L\boldsymbol{I}$
上式的完整证明很复杂,但事实上与定理4大部分是相同的,(d)的右边略有不同,下面简要证明一下。考虑带积分余项的0阶Taylor展开:
$$ f(\boldsymbol{x})=f(\boldsymbol{x}_0)+\left\langle \int_{0}^{1} \nabla f(\boldsymbol{x}_0+\theta(\boldsymbol{x}-\boldsymbol{x}_0)) {\rm d}\theta,\ \boldsymbol{x}-\boldsymbol{x}_0 \right\rangle\tag{11} $$
为了简化表述,我们记:$\boldsymbol{x}_\alpha=\alpha \boldsymbol{x}+(1-\boldsymbol{\alpha})\boldsymbol{y}$,则:
$$ \begin{aligned} f(\boldsymbol{x})-f\left(\boldsymbol{x}_{\alpha}\right) &=\left\langle\int_{0}^{1} \nabla f \left(\boldsymbol{x}_{\alpha}+\theta(\boldsymbol{x}-\boldsymbol{x}_{\alpha})\right) {\rm d} \theta, \boldsymbol{x}-\boldsymbol{x}_{\alpha} \right\rangle \\ &= \left\langle\int _ { 0 } ^ { 1 } \nabla f \left( \boldsymbol{x}_{\alpha}+\theta(\boldsymbol{x}-\boldsymbol{x}_{\alpha})\right) {\rm d} \theta,\ (1-\alpha)(\boldsymbol{x}-\boldsymbol{y})\right\rangle \\ f(\boldsymbol{y})-f\left(\boldsymbol{x}_{\alpha}\right) &=\left\langle\int_{0}^{1} \nabla f \left(\boldsymbol{x}_{\alpha}+\theta(\boldsymbol{y}-\boldsymbol{x}_{\alpha})\right) {\rm d} \theta, \boldsymbol{y}-\boldsymbol{x}_{\alpha} \right\rangle \\ &= \left\langle\int _ { 0 } ^ { 1 } \nabla f \left( \boldsymbol{x}_{\alpha}+\theta(\boldsymbol{y}-\boldsymbol{x}_{\alpha})\right) {\rm d} \theta,\ \alpha(\boldsymbol{y}-\boldsymbol{x})\right\rangle \end{aligned} $$
所以:
$$ \begin{align} &\alpha f(\boldsymbol{x}) + (1-\alpha)f(\boldsymbol{y}) - f\left( \alpha \boldsymbol{x} + (1-\alpha)\boldsymbol{y} \right)\\ &=\alpha(f(\boldsymbol{x})-f(\boldsymbol{x}_\alpha))+(1-\alpha)(f(\boldsymbol{y})-f(\boldsymbol{x}_\alpha))\\ &= \alpha(1-\alpha) \left\langle \boldsymbol{y}-\boldsymbol{x},\ \int _ { 0 } ^ { 1 } \left[ \nabla f \left( \boldsymbol{x}_{\alpha}+\theta(\boldsymbol{y}-\boldsymbol{x}_{\alpha})\right) - \nabla f \left( \boldsymbol{x}_{\alpha}+\theta(\boldsymbol{x}-\boldsymbol{x}_{\alpha})\right) \right] {\rm d} \theta \right\rangle \\ &\leq \alpha(1-\alpha) \| \boldsymbol{y}-\boldsymbol{x} \| \int _ { 0 } ^ { 1 } L\| \boldsymbol{y}-\boldsymbol{x} \| \theta {\rm d} \theta = \frac{\alpha(1-\alpha)L}2 \| \boldsymbol{y}-\boldsymbol{x} \|^2 \end{align} $$
定理6:强凸性与Lipschitz光滑性的其他性质
(1)设有函数$h(\boldsymbol{x}) = f(\boldsymbol{x}) - \frac{\mu}{2}||\boldsymbol{x}||^2$,则:
- $f$是$\mu$-强凸的当且仅当$h$是凸的。
- 进一步,若$f$还是$L$-光滑的,则$h$是 $(L-\mu)$-光滑的。
(2)若$f$是$\mu$-强凸且是$L$-光滑的,则:
$$ \left\langle \nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x}),\boldsymbol{y}-\boldsymbol{x} \right\rangle \leq \frac{\mu L}{\mu+L} \left\| \boldsymbol{y}-\boldsymbol{x} \right\|^2 + \frac{1}{\mu+L} \left\| \nabla f(\boldsymbol{y}) - \nabla f(\boldsymbol{x}) \right\|^2 $$
证明:
若$\mu=L$,则两边都取等号;若$\mu<L$,则取凸函数$h(x) = f(x) - \frac \mu2 \| x \|^2$,由定理6(1)知$h$是$(L-\mu)$-光滑的,由定理5(c)左半部分知:
$$ \left\langle \nabla h(\boldsymbol{y}) - \nabla h(\boldsymbol{x}),\boldsymbol{y}-\boldsymbol{x} \right\rangle \geq \frac 1{L-\mu} \left\| \nabla h(\boldsymbol{y})-\nabla h(\boldsymbol{x}) \right\|^2 $$
化简即得定理6(2)。
在优化问题中的讨论
上面说了这么多,那么我们究竟为什么要研究强凸性与Lipschitz光滑呢?
从直观与梯度层面
若$f$是$\mu$-强凸的,则由定理4(B),$f$有一个二次函数下界:
$$ f(\boldsymbol{x}_0) + \left\langle\nabla f(\boldsymbol{x}_0), \boldsymbol{x}-\boldsymbol{x}_0\right\rangle + \frac{\mu}{2}\|\boldsymbol{x}-\boldsymbol{x}_0\|^2 \leqslant f(\boldsymbol{x}) $$
若$f$是$L$-光滑的,则由定理5(b),$f$有一个二次函数上界:
$$ f(\boldsymbol{x}) \leqslant f(\boldsymbol{x}_0) + \left\langle\nabla f(\boldsymbol{x}_0), \boldsymbol{x}-\boldsymbol{x}_0\right\rangle + \frac{L}{2}\|\boldsymbol{x}-\boldsymbol{x}_0\|^2 $$
所以,若$f$同时满足强凸性与Lipschitz光滑性,则$f$被“框”在两个二次函数之间:
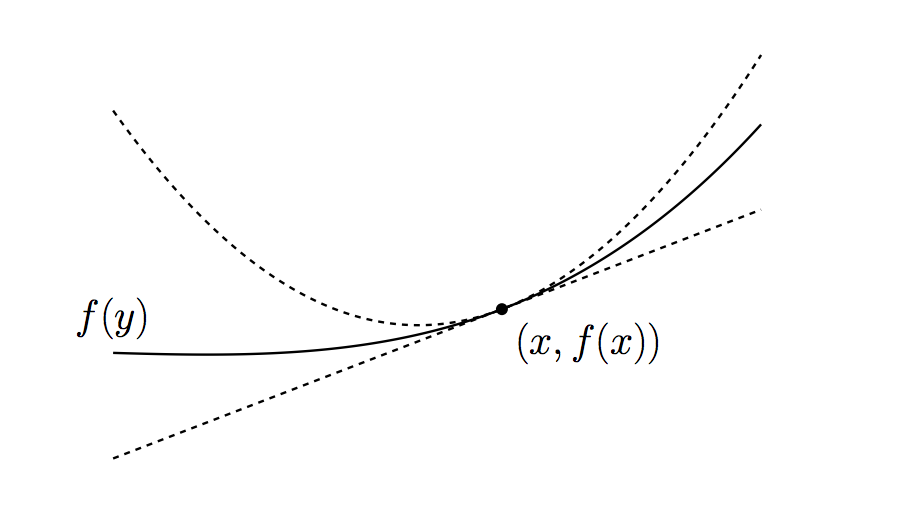
此外,由定理4(C)与定义2可知:
$$ \mu \|\boldsymbol{y}-\boldsymbol{x} \|\leq \|\nabla f(\boldsymbol{y})-\nabla f(\boldsymbol{x}) \|\leq L\|\boldsymbol{y}-\boldsymbol{x} \| $$
函数梯度的变化既不会太大又不会太小,这极大简化了很多证明算法收敛性和估计收敛率的情况。
从凸优化的层面
考虑无约束优化问题:
$$ \min f(\boldsymbol{x})\tag{*} $$
若若$f$是$\mu$-强凸的且是$L$-光滑的,则显然(*)是一个凸问题,设其的一个最优解为$\boldsymbol{x}^*$,最优值即为$f(\boldsymbol{x}^*)$,则我们有:
定理7:Polyak-Lojasiewicz(PL)条件
$$ \begin{align} \frac{1}{2L}\|\nabla f(\boldsymbol{x})\|^2 \leq f(\boldsymbol{x}) &- f(\boldsymbol{x}^*) \leq \frac{L}{2}\|\boldsymbol{x}-\boldsymbol{x}^*\|^2\tag{a}\\ \frac{\mu}{2}\|\boldsymbol{x}-\boldsymbol{x}^*\|^2 \leq f(\boldsymbol{x}) &- f(\boldsymbol{x}^*) \leq \frac{1}{2\mu}\|\nabla f(\boldsymbol{x})\|^2\tag{b} \end{align} $$
对于凸问题而言,则从三个方面刻画了最优解与最优值的相关性能。
证明:
我们先来看(a)。由$\boldsymbol{x}^*$是最优解,则必有$\|\nabla f(\boldsymbol{x}^*) \|=0$,由定理5(b)知:
$$ f(\boldsymbol{x})-f(\boldsymbol{x}^*) - \left\langle \nabla f(\boldsymbol{x}),\ \boldsymbol{x}-\boldsymbol{x}^* \right\rangle \leq \frac L2 \left\| \boldsymbol{x}-\boldsymbol{x}^* \right\|^2 $$
对于(a)的左半部分,我们注意到:
$$ \begin{align*} f(\boldsymbol{x}^*) &= \min_\boldsymbol{x} f(\boldsymbol{x})&\\ &\leq \min_\boldsymbol{x}\left[f(\boldsymbol{z}) + \left\langle\nabla f(\boldsymbol{z}),(\boldsymbol{x}-\boldsymbol{z})\right\rangle + \frac{L}{2}\|\boldsymbol{x}-\boldsymbol{z}\|^2\right] &定理5(b)\\ &= f(\boldsymbol{z}) + \min_{||\boldsymbol{e}||=1}\min_{t\geq0}\left[\left\langle\nabla f(\boldsymbol{z}),\boldsymbol{e}\right\rangle\cdot t + \frac{L}{2}t^2\right]&t=\|\boldsymbol{x}-\boldsymbol{z}\|\\ &= f(\boldsymbol{z}) + \min_{||\boldsymbol{e}||=1}\left[-\frac{(\left\langle\nabla f(\boldsymbol{z}),\boldsymbol{e}\right\rangle)^2}{2L}\right]&\\ &= f(\boldsymbol{z}) - \frac{||\nabla f(\boldsymbol{z})||^2}{2L}& \end{align*} $$
对于(b),左半部分由定理4(B)易证,对于右边则与(a)左半部分证明相同,只需把$\leq$换成$\geq$即可。

1 条评论
写得真好!