系列文章
1、仿射集与凸集
1.1:引入
我们知道,在 $\mathbb{R}^n$中的两点 $\boldsymbol{x}_1,\boldsymbol{x}_2$唯一确定一条过这两点的线段(直线)。具体而言,取 $\theta\in[0,1]$,则这条线段可表示为:$\boldsymbol{y}=\theta\boldsymbol{x}_1+(1-\theta)\boldsymbol{x}_2$,而当$\theta\in\mathbb{R}$时,则直线为:$\boldsymbol{y}=\theta\boldsymbol{x}_1+(1-\theta)\boldsymbol{x}_2=\boldsymbol{x}_2+\theta(\boldsymbol{x}_1-\boldsymbol{x}_2)$。
1.2:仿射集
定义1.1.2.1:仿射集
设一集合$\boldsymbol{C}\subseteq\mathbb{R}^n$,若$\forall \boldsymbol{x}_1,\boldsymbol{x}_2\in\boldsymbol{C}$,连接$\boldsymbol{x}_1$与$\boldsymbol{x}_2$的直线也在$\boldsymbol{C}$内,即$\theta\boldsymbol{x}_1+(1-\theta)\boldsymbol{x}_2\in\boldsymbol{C},\theta\in\mathbb{R}$,则称$\boldsymbol{C}$为仿射集。
例如直线、$\mathbb{R}^n$是仿射集,而线段、闭合图形不是
定义1.1.2.2:仿射组合
设有集合$\boldsymbol{C}$中的k个点:$\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k$,设$\theta_1,\cdots,\theta_k\in\mathbb{R},\sum_{i=1}^k \theta_i=1$,则称$\sum_{i=1}^k \theta_i\boldsymbol{x}_i$为$\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k$的仿射组合
定理1.1.2.1
若$\boldsymbol{C}$是一仿射集,则$\boldsymbol{C}$中任意k个点$\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k$的仿射组合也在$\boldsymbol{C}$中。
定理1.1.2.2
任意线性方程组的解集是仿射集;任意仿射集可以表示为一线性方程组的解集。
1.3:仿射包
给定集合$\boldsymbol{C}$,如何构造一个包含$\boldsymbol{C}$的最小仿射集?
定义1.1.3.1:仿射包
设有集合$\boldsymbol{C}$,称$\boldsymbol{C}$中点的所有仿射组合构成的集合为$\boldsymbol{C}$的仿射包,记为$\text{aff}\ \boldsymbol{C}$,即:
$$ \text{aff}\ \boldsymbol{C}=\{\sum\limits_{i=1}^k \theta_i\boldsymbol{x}_i|\boldsymbol{x}_i\in\boldsymbol{C},\sum_{i=1}^k \theta_i=1,\theta_i\in\mathbb{R}\} $$
1.4:凸集
定义1.1.4.1:凸集
设一集合$\boldsymbol{C}\subseteq\mathbb{R}^n$,若$\forall \boldsymbol{x}_1,\boldsymbol{x}_2\in\boldsymbol{C}$,连接$\boldsymbol{x}_1$与$\boldsymbol{x}_2$的线段也在$\boldsymbol{C}$内,即$\theta\boldsymbol{x}_1+(1-\theta)\boldsymbol{x}_2\in\boldsymbol{C},\theta\in[0,1]$,则称$\boldsymbol{C}$为凸集。
显然,凸集是在仿射集上加了$\theta\in[0,1]$的条件,故而凸集是特殊的仿射集。类似地,我们有如下定义:
定义1.1.4.2:凸组合
我们称$\sum \theta_i\boldsymbol{x}_i,\theta_i\in[0,1],\sum \theta_i=1$为一凸组合
定义1.1.4.3:凸包
凸集中所有凸组合构成的集合称为凸包,记为$\text{conv}\ \boldsymbol{C}$。
1.5:锥
定义1.1.5.1:锥
设有集合$\boldsymbol{C}$,若$\forall \boldsymbol{x}\in\boldsymbol{C},\theta\geq 0$,有:$\theta\boldsymbol{x}\in\boldsymbol{C}$,则称$\boldsymbol{C}$是锥。
定义1.1.5.2:凸锥
设有集合$\boldsymbol{C}$,若$\forall \boldsymbol{x}_1,\boldsymbol{x}_2\in\boldsymbol{C},\theta_1,\theta_2\geq 0$,有:$\theta_1\boldsymbol{x}_1+\theta_2\boldsymbol{x}_2\in\boldsymbol{C}$,则称$\boldsymbol{C}$是凸锥。
定义1.1.5.3:凸锥组合
称$\sum \theta_i\boldsymbol{x}_i,\theta_i\geq0$为$\boldsymbol{x}_1,\cdots,\boldsymbol{x}_k$的凸锥组合。同样我们也有凸锥包的概念。
由锥与凸锥的定义,显然锥与凸锥都包含$\boldsymbol{0}$。
1.6:几个重要的例子
下图总结了几个重要的例子:

1.7:超平面与半空间
定义1.1.7.1:超平面与半空间
设有$\boldsymbol{a}\in\mathbb{R}^n,\boldsymbol{a}\neq\boldsymbol{0},\boldsymbol{b}\in\mathbb{R}$,则集合$\boldsymbol{A}=\{\boldsymbol{x}|\boldsymbol{a}^\top\boldsymbol{x}=b\}$称为一个$n$维超平面。显然它是仿射集、凸集,当$\boldsymbol{0}\in\boldsymbol{A}$是它还是凸锥。
$\boldsymbol{A}$将$\mathbb{R}^n$分为了两个部分,我们称之为半空间。具体地,这两个半空间分别就是$\boldsymbol{a}^\top\boldsymbol{x}<b$与$\boldsymbol{a}^\top\boldsymbol{x}>b$的解空间。
1.8:球与椭球
定义1.1.8.1:球
$\mathbb{R}^n$中的球定义为:
$$ \mathcal{B}(\boldsymbol{x}_c,r)=\{\boldsymbol{x}|||\boldsymbol{x}-\boldsymbol{x}_c||_2^2\leq r\} $$
其中,我们称$\boldsymbol{x}_c$为球心,$r$为半径。
定理1.1.8.1:球是一个凸集
证略。
定义1.1.8.2:椭球
$\mathbb{R}^n$中的椭球定义为:
$$ \mathcal{E}(\boldsymbol{x}_c,\boldsymbol{P})=\{\boldsymbol{x}|(\boldsymbol{x}-\boldsymbol{x}_c)^\top\boldsymbol{P^{-1}(\boldsymbol{x}-\boldsymbol{x}_c)}\leq1\} $$
其中$\boldsymbol{P}$为(对称)正定阵。特别地,球可以看做$\boldsymbol{P}=r^2\boldsymbol{I}$的椭球。可以证明,椭球也是一个凸集。
矩阵$\boldsymbol{P}$决定了椭球从$\boldsymbol{x}_c$向各个方向扩展的幅度,事实上$\boldsymbol{P}$的$n$个特征值的开方$\sqrt{\lambda_i}$就是椭球的$n$个半轴长。
一个$\mathbb{R}^2$上的椭球例子如下:
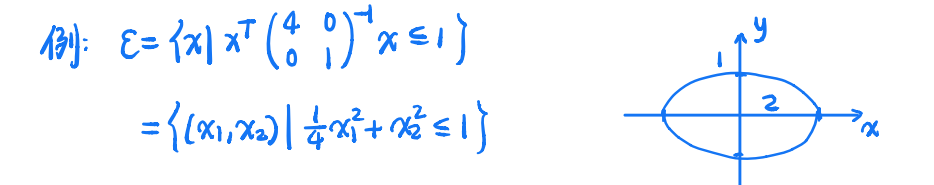
1.9:多面体
定义1.1.9.1:多面体
有限个线性不等式与等式的解空间称为多面体:
$$ \mathcal{P}=\{\boldsymbol{x}|\boldsymbol{a}^\top_i\boldsymbol{x}\leq b_i,\boldsymbol{c}_j^\top\boldsymbol{x}=d_j\} $$
所以多面体事实上是若干超平面与半空间的交集。可以证明,有界多面体一定是凸集。
1.10:单纯形
定义1.1.10.1:单纯形
在$\mathbb{R}^n$中选择$k+1$个点:$\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k$,其满足:$\boldsymbol{v}_1-\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k-\boldsymbol{v}_0$线性无关,则与这$k+1$个点相关的单纯形为:
$$ \boldsymbol{C}=\text{conv}\{\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k\}=\{\sum_{i=0}^k \theta_i\boldsymbol{v}_i|\theta_i\geq0,\sum_{i=1}^k \theta_i=1\} $$
例如$\mathbb{R}^2$上的线段、三角形(包括内部),$\mathbb{R}^3$上的四面体
定理1.1.10.1:单纯形是多面体
证明:
在$\mathbb{R}^n$中选择$k+1$个点:$\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k$,其满足:$\boldsymbol{v}_1-\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k-\boldsymbol{v}_0$线性无关,记与这$k+1$个点相关的单纯形为:$\boldsymbol{C}$。设$\boldsymbol{x}\in\boldsymbol{C}$,即存在$\boldsymbol{\theta}\in\mathbb{R}^{k+1}$,$\theta_i\geq0$且$\boldsymbol{1}^\top\boldsymbol{\theta}=1$。
我们定义向量:$\boldsymbol{y}=[\theta_1,\cdots,\theta_k]\in\mathbb{R}^k$,定义矩阵$\boldsymbol{B}$的列组为$\{\boldsymbol{v}_1-\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k-\boldsymbol{v}_0\}$,即:
$$ \boldsymbol{B}=\begin{bmatrix} \boldsymbol{v}_1-\boldsymbol{v}_0,\cdots,\boldsymbol{v}_k-\boldsymbol{v}_0 \end{bmatrix}_{n\times k} $$
所以,$\boldsymbol{x}$可写为:
$$ \boldsymbol{x}=\boldsymbol{v}_0+\boldsymbol{By}\tag{1} $$
由题易知$\boldsymbol{B}$是列满秩的:$\text{rank}(\boldsymbol{B})=k$($k\leq n$!),故而一定存在非奇异阵$\boldsymbol{A}\in\mathbb{R}^{n\times n}$使得:
$$ \boldsymbol{AB}=\begin{bmatrix} \boldsymbol{I}_k\\ \boldsymbol{O}_{(n-k)\times k} \end{bmatrix} $$
我们不妨将$\boldsymbol{A}$写成分块矩阵的形式:$\begin{bmatrix}\boldsymbol{A}_1\\ \boldsymbol{A}_2\end{bmatrix}$,其中$\boldsymbol{A}_1\in\mathbb{R}_{k\times n}$。在(1)式左右两边同时左乘$\boldsymbol{A}$,则:
$$ \boldsymbol{A}_1\boldsymbol{x}=\boldsymbol{A}_1\boldsymbol{v}_0+\boldsymbol{y},\ \boldsymbol{A}_2\boldsymbol{x}=\boldsymbol{A}_2\boldsymbol{v}_0\tag{2} $$
我们引入记号:$\preccurlyeq$,$\boldsymbol{\alpha}\preccurlyeq\boldsymbol{\beta}\Leftrightarrow \alpha_i\leq \beta_i$,所以:$\boldsymbol{0}\preccurlyeq\boldsymbol{y}\preccurlyeq\boldsymbol{1}$,从而由(2)有:
$$ \boldsymbol{A}_2\boldsymbol{x}=\boldsymbol{A}_2\boldsymbol{v}_0,\ \boldsymbol{A}_1\boldsymbol{v}_0\preccurlyeq\boldsymbol{A}_1\boldsymbol{x},\ \boldsymbol{1}^\top\boldsymbol{A}_1\boldsymbol{x}\leq1+\boldsymbol{1}^\top\boldsymbol{A}_1\boldsymbol{v}_0 $$
显然,这描述了一个多面体。
1.11:正定矩阵集合
定义1.1.11.1:
我们考虑以下集合:
- 对称矩阵集合:$\boldsymbol{S}^n=\{\boldsymbol{X}|\boldsymbol{X}\in\mathbb{R}^{n\times n},\boldsymbol{X}=\boldsymbol{X}^\top\}$
- 半正定矩阵集合:$\boldsymbol{S}^n_+=\{\boldsymbol{X}|\boldsymbol{X}\in\boldsymbol{S}^n,\boldsymbol{X}\succeq0\}$
- 正定矩阵集合:$\boldsymbol{S}^n_{++}=\{\boldsymbol{X}|\boldsymbol{X}\in\boldsymbol{S}^n,\boldsymbol{X}\succ0\}$
定理1.11.1:$\boldsymbol{S}^n_{+}$是凸集且是凸锥
2、保凸运算
注意!这里的保凸运算指一个凸集经过某种运算、映射后仍为一凸集,与第二章凸函数部分的保凸运算不同!
2.1:交集
定理1.2.1.1:交集操作保凸
设有两个凸集$\boldsymbol{S}_1,\boldsymbol{S}_2$,则$\boldsymbol{S}_1\cap\boldsymbol{S}_2$是凸的。推而广之,无穷多个凸集的交集也是一个凸集。
2.2:仿射函数
定义1.2.2.1:仿射函数
设有$f:\mathbb{R}^n\to\mathbb{R}^m$,若$f$具有形式:$f(\boldsymbol{x})=\boldsymbol{Ax}+\boldsymbol{b}$,其中$\boldsymbol{A}\in\mathbb{R}^{m\times n},\boldsymbol{b}\in\mathbb{R}^m$,则称$f$为仿射的。
例如:伸缩$a\boldsymbol{x}$平移$\boldsymbol{x}+\boldsymbol{b}$是仿射的。
定理1.2.2.1:仿射函数保凸
设有仿射函数$f:\mathbb{R}^n\to\mathbb{R}^m$,与凸集$\boldsymbol{C}\subseteq\mathbb{R}^n$,则集合$f(\boldsymbol{C})=\{f(\boldsymbol{x})|\boldsymbol{x}\in\boldsymbol{C}\}$是凸集。相应地,凸集$\boldsymbol{S}\in\mathbb{R}^m$在$f$下的原象$f^{-1}(\boldsymbol{S})=\{x|f(\boldsymbol{x}\in\boldsymbol{S})\}$也是凸的。
例如:椭球是球的仿射映射。设有:$\mathcal{B}=\{\boldsymbol{u}|||\boldsymbol{u}||_2\leq 1\},\mathcal{E}=\{\boldsymbol{x}|(\boldsymbol{x}-\boldsymbol{x}_c)^\top\boldsymbol{P}^{-1}(\boldsymbol{x}-\boldsymbol{x}_c)\}$,其中$\boldsymbol{P}\in\boldsymbol{S}^n_{++}$。试求一仿射函数$f$使得$f(\mathcal{B})=\mathcal{E}$。
解:
由$\boldsymbol{P}\in\boldsymbol{S}^n_{++}$,故而$\boldsymbol{P}$一定可正交对角化:$\boldsymbol{O}^{-1}\boldsymbol{PO}=\boldsymbol{D}=\text{diag}(\lambda_1,\cdots,\lambda_n)$,由$\boldsymbol{P}$正定,则可取矩阵$\boldsymbol{D}_1=\text{diag}(\sqrt{\lambda_1},\cdots,\sqrt{\lambda_n}),\boldsymbol{Q}=\boldsymbol{O}^{-1}\boldsymbol{D}_1\boldsymbol{O}$,易知$\boldsymbol{Q}^2=\boldsymbol{QQ}=\boldsymbol{P}$,且它是正定的。
取映射:$f:\mathbb{R}^n\to\mathbb{R}^n,f(\boldsymbol{u})=\boldsymbol{Qu}+\boldsymbol{x}_c$,此时,$f(\mathcal{B})=\{f(\boldsymbol{u})|||\boldsymbol{u}||^2\leq1\}=\mathcal{E}$。
2.3:透视函数
定义1.2.3.1:透视函数
设有映射$P:\mathbb{R}^{n+1}\to\mathbb{R}^n$,其定义域为:$\text{dom}P=\mathbb{R}^n\times \mathbb{R}_+$,即$P(\boldsymbol{z},t)$,$\boldsymbol{z}\in\mathbb{R}^n,t>0$。若$P(\boldsymbol{z},t)=\boldsymbol{z}/t$,则称$P$为一透视函数。
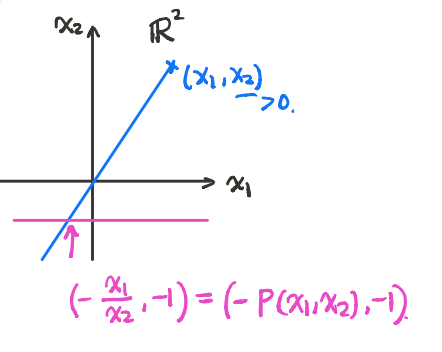
我们以小孔成像的例子来理解。取透视函数$P:(x_1,x_2)\mapsto x_1/x_2$,它可以理解为点$(x_2,x_1)$透过原点后在$x_2=-1$上的象横坐标的相反数:
定理1.2.3.1:透视函数保凸
设有凸集$\boldsymbol{C}\subseteq\text{dom}P$,则$P(\boldsymbol{C})=\{P(x)|x\in\boldsymbol{C}\}$也是凸集。
2.4:线性分式函数
定义1.2.4.1:线性分式(分数)函数
线性分式函数有透视函数和仿射函数复合而成。具体地,设有仿射映射:
$$ g:\mathbb{R}^n\to\mathbb{R}^{m+1},g(\boldsymbol{x})=\begin{bmatrix} \boldsymbol{A}_{m\times n}\\ (\boldsymbol{c}^\top)_{1\times n} \end{bmatrix}\boldsymbol{x}+\begin{bmatrix} \boldsymbol{b}^{m\times 1}\\ d \end{bmatrix} $$
与一透视变换:$P:\mathbb{R}^{m+1}\to\mathbb{R}^m$,则线性分式函数$f:\mathbb{R}^n\to\mathbb{R}^m$定义为:$f=P\circ g$,具体地:
$$ f(\boldsymbol{x})=\frac{\boldsymbol{Ax}+\boldsymbol{b}}{\boldsymbol{c}^\top\boldsymbol{x}+d},\ \text{dom}f=\{\boldsymbol{x}|\boldsymbol{c}^\top\boldsymbol{x}+d>0\} $$
定理1.2.4.1:线性分式函数保凸
设有一线性分式函数$f$,有一凸集$\boldsymbol{C}\subseteq\text{dom}f$,则$f(\boldsymbol{C})$也是凸集。