前言
本章讨论实值标量函数、实值向量函数、实值矩阵函数对于实向量变元、矩阵变元的偏导,函数变元为复向量复矩阵的微分这里就不介绍了。
系列文章
0、符号
为了方便理解,我们对变量与函数作一下规定:
- 实向量变元:$\boldsymbol{x}=\left[x_1,\cdots,x_m\right]^\top\in\mathbb{R}^m$
- 实矩阵变元:$\boldsymbol{X}=\left[\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n\right]\in\mathbb{R}^{m\times n}$
- 变元为向量的实值标量函数:$f(\boldsymbol{x})\in\mathbb{R}$,记为 $f:\mathbb{R}^m\to \mathbb{R}$
- 变元为矩阵的实值标量函数:$f(\boldsymbol{X})\in\mathbb{R}$,记为 $f:\mathbb{R}^{m\times n}\to\mathbb{R}$
- 变元为向量的 $p$ 维实列向量函数:$\boldsymbol{f}(\boldsymbol{x})\in\mathbb{R}^p$,记为 $\boldsymbol{f}:\mathbb{R}^m\to\mathbb{R}^p$
- 变元为矩阵的 $p$ 维实列向量函数:$\boldsymbol{f}(\boldsymbol{X})\in\mathbb{R}^p$,记为 $\boldsymbol{f}:\mathbb{R}^{m\times n}\to\mathbb{R}^p$
- 变元为向量的 $p\times q$维实矩阵函数:$\boldsymbol{F}(\boldsymbol{x})\in\mathbb{R}^{p\times q}$,记为 $\boldsymbol{F}:\mathbb{R}^{m}\to\mathbb{R}^{p\times q}$
- 变元为矩阵的 $p\times q$维实矩阵函数:$\boldsymbol{F}(\boldsymbol{X})\in\mathbb{R}^{p\times q}$,记为 $\boldsymbol{F}:\mathbb{R}^{m\times n}\to\mathbb{R}^{p\times q}$
事实上,所谓的向量函数或矩阵函数即是若干标量函数排列成向量或矩阵的形式,也即:
$$ \begin{align} \boldsymbol{f}(\boldsymbol{X})&= \begin{bmatrix} f_1(\boldsymbol{X})\\ \vdots\\ f_p(\boldsymbol{X}) \end{bmatrix}\\ \boldsymbol{F}(\boldsymbol{X})&= \begin{bmatrix} F_{11}(\boldsymbol{X})&\cdots &F_{1q}(\boldsymbol{X})\\ \vdots &\ddots & \vdots \\F_{p1}(\boldsymbol{X})&\cdots & F_{pq}(\boldsymbol{X}) \end{bmatrix} \end{align} $$
1、Jacobian 矩阵与梯度矩阵
1.1:Jacobian 矩阵
很多时候我们需要求解函数的微分,实质上是对每个元素求偏导。而当变元是向量或矩阵时由于偏导数太多故而需要合理组织,于是便引入了 Jacobian 矩阵,换句话说 Jacobian 矩阵可以被视为一个组织偏导数的矩阵,其行列式称为 Jacobian 行列式。
(1)标量函数
我们首先来看最简单的情况:变元为 $m\times 1$维向量 $\boldsymbol{x}$的处处可微实值标量函数 $f:\mathbb{R}^m\to\mathbb{R}$。事实上这部分就是数分中多元函数微分学的内容,我们复习一下。
设有一方向 $\boldsymbol{u}$,$\boldsymbol{x}_0\in\mathbb{R}^m$,若极限
$$ \lim\limits_{t\to 0} \frac{f(\boldsymbol{x}_0+t\boldsymbol{u})-f(\boldsymbol{x}_0)}{t} $$
存在且有限,则称之为 $f$在点 $\boldsymbol{x}_0$处沿方向 $\boldsymbol{u}$的方向导数,记为 $\frac{\partial f}{\partial \boldsymbol{u}}(\boldsymbol{x}_0)$。特别地,当 $\boldsymbol{u}$为单位向量 $\boldsymbol{e}_i$时,称$f$在点 $\boldsymbol{x}_0$处沿方向 $\boldsymbol{e}_i$的方向导数为 $f$在 $\boldsymbol{x}_i$处的第 $i$个一阶偏导数,记为 $\frac{\partial f}{\partial x_i}(\boldsymbol{x}_0)$或 $\text{D}_{x_i}(\boldsymbol{x}_0)$,抽象地,我们可以引出偏微分算子:$\text{D}_{x_i}=\frac{\partial}{\partial x_i}$。
我们知道,若在 $\boldsymbol{x}_0$处给定一增量:$\boldsymbol{h}=\left[h_1,\cdots,h_m\right],||\boldsymbol{h}||_2\to 0$,则 $f$在 $\boldsymbol{x}_0$处的全微分为:
$$ \text{d}f(\boldsymbol{x}_0)=\sum\limits_{i=1}^m \frac{\partial f}{\partial x_i}(\boldsymbol{x}_0)h_i $$
也即:
$$ \text{d}f(\boldsymbol{x}_0)=\left[\text{D}_{x_1}(\boldsymbol{x}_0),\cdots,\text{D}_{x_m}(\boldsymbol{x}_0)\right]\boldsymbol{h} $$
所以自然地,我们可以引出偏导算子:
$$ \text{D}_{\boldsymbol{x}}\overset{\underset{\mathrm{def}}{}}{=}\frac{\partial}{\partial \boldsymbol{x}^\top}=\left[\text{D}_{x_1},\cdots,\text{D}_{x_m}\right]=\left[\frac{\partial}{\partial x_1},\cdots,\frac{\partial}{\partial x_m}\right] $$
同时我们称矩阵 $\left[\text{D}_{x_1}(\boldsymbol{x}_0),\cdots,\text{D}_{x_m}(\boldsymbol{x}_0)\right]_{1\times m}$为 $f$在 $\boldsymbol{x}_0$处的 Jacobian 矩阵,记为 $\text{D}_{\boldsymbol{x}}f(\boldsymbol{x}_0)$。有时在不引起歧义的情况下提到 Jacobian 矩阵时,其也被记为 $\boldsymbol{J}$。
练习:自变量为$m$维列向量,其第 $i$个分量记为 $x_i$。设 $f(\boldsymbol{x})=\sum\limits_{i=1}^m a_ix_i^2$,求解其在 $\boldsymbol{x}_0=\left[c_1,\cdots,c_m\right]^\top$ 处的 Jacobian 矩阵。
现在我们来看变元为矩阵的实值标量函数:$f:\mathbb{R}^{m\times n}\to\mathbb{R}$。自然地,$f(\boldsymbol{X})$在 $\boldsymbol{X}$处的 Jacobian 矩阵:
$$ \text{D}_{\boldsymbol{X}}f(\boldsymbol{X})=\frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}^{\color{red}{\top}}}=\begin{bmatrix} \frac{\partial f(\boldsymbol{X})}{\partial x_{11}} & \cdots & \frac{\partial f(\boldsymbol{X})}{\partial x_{m1}}\\ \vdots & \ddots & \vdots \\ \frac{\partial f(\boldsymbol{X})}{\partial x_{1n}} & \cdots &\frac{\partial f(\boldsymbol{X})}{\partial x_{mn}} \end{bmatrix}_{\color{Red}{n\times m}} $$
当然我们还有另外一种思路,在向量化与矩阵化中我们介绍了将矩阵转换为向量的向量化算子 $\text{vec}$与行向量化算子 $\text{rvec}$,自然想到可将矩阵变元向量化,再结合上文关于变元为向量的标量函数的讨论得到 Jacobian 矩阵:
$$ \text{D}_{\text{vec}\boldsymbol{X}}f(\boldsymbol{X})=\frac{\partial f(\boldsymbol{X})}{\partial \text{vec}^\top (\boldsymbol{X})}=\left[\frac{\partial f(\boldsymbol{X})}{\partial x_{11}},\cdots,\frac{\partial f(\boldsymbol{X})}{\partial x_{m1}},\cdots,\frac{\partial f(\boldsymbol{X})}{\partial x_{1n}},\cdots,\frac{\partial f(\boldsymbol{X})}{\partial x_{mn}}\right]_{1\times mn} $$
考虑这两种定义,有:
$$ \text{D}_{\text{vec}\boldsymbol{X}}f(\boldsymbol{X})=\text{rvec}(\text{D}_{\boldsymbol{X}}f(\boldsymbol{X}))=\text{vec}^\top(\text{D}_{\boldsymbol{X}}f(\boldsymbol{X})) $$
(2)向量函数
在研究完标量函数后,我们来看向量函数。首先研究变元为向量的向量函数 $\boldsymbol{f}:\mathbb{R}^m\to\mathbb{R}^p$。显然地,我们可以把 $\boldsymbol{f}$拆解为 $p$个标量函数的组合:
$$ \boldsymbol{f}(\boldsymbol{x})=\begin{bmatrix} f_1(\boldsymbol{x})\\ \vdots\\ f_p(\boldsymbol{x})\end{bmatrix} $$
显然,$p$个子函数有 $p$个 $1\times m$ 维的 Jacobian 矩阵$\boldsymbol{J}_1,\cdots,\boldsymbol{J}_p$,按列堆叠,则即得$\boldsymbol{f}(\boldsymbol{x})$ 的$p\times m$ 维的 Jacobian 矩阵:
$$ \text{D}_{\boldsymbol{x}}\boldsymbol{f}(\boldsymbol{x})=\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial \boldsymbol{x}^\top}=\begin{bmatrix} \frac{\partial f_1(\boldsymbol{x})}{\partial x_1} & \cdots & \frac{\partial f_1(\boldsymbol{x})}{\partial x_m}\\ \vdots & \ddots & \vdots\\ \frac{\partial f_p(\boldsymbol{x})}{\partial x_1}&\cdots &\frac{\partial f_p(\boldsymbol{x})}{\partial x_m} \end{bmatrix}_{p\times m} $$
相应地,对于变元为矩阵的向量函数 $\boldsymbol{f}:\mathbb{R}^{m\times n}\to\mathbb{R}^p$,我们可以将变元向量化再应用上文的结论,得到的 Jacobian 矩阵是 $p\times mn$维的,具体形式:
$$ \text{D}_{\text{vec}\boldsymbol{X}}\boldsymbol{f}(\boldsymbol{X})= \begin{bmatrix} \frac{\partial f_1(\boldsymbol{X})}{\partial x_{11}} & \cdots &\frac{\partial f_1(\boldsymbol{X})}{\partial x_{m1}} & \cdots &\frac{\partial f_1(\boldsymbol{X})}{\partial x_{1n}} &\cdots \frac{\partial f_1(\boldsymbol{X})}{\partial x_{mn}}\\ \vdots & \ddots &\vdots & \ddots &\vdots & \ddots\\ \frac{\partial f_p(\boldsymbol{X})}{\partial x_{11}} & \cdots &\frac{\partial f_p(\boldsymbol{X})}{\partial x_{m1}} & \cdots &\frac{\partial f_p(\boldsymbol{X})}{\partial x_{1n}} &\cdots \frac{\partial f_p(\boldsymbol{X})}{\partial x_{mn}} \end{bmatrix}_{p\times mn} $$
练习:设有一球坐标系 $M(\rho,\phi,\theta)$,原点 $O$,$\rho=||\overrightarrow{O M}||_2$,$\phi$是 $\overrightarrow{O M}$与 $z$轴正向的夹角,$\theta$是向量 $\overrightarrow{O M}$在平面 $xOy$上投影与 $x$轴正向的夹角。考虑球坐标系到直角坐标系的变换:$f:\mathbb{R}_+\cup\{0\}\times [0,\pi)\times [0,2\pi)\to \mathbb{R}^3$,其中:
$$ \begin{align} x&=\rho\sin{\phi}\cos{\theta}\\ y&=\rho\sin{\phi}\sin{\theta}\\ z&=\rho\cos{\phi} \end{align} $$
试求该变换在点 $M(\rho,\phi,\theta)$处的 Jacobian 矩阵。
(3)矩阵函数
考虑变元为矩阵的矩阵函数 $\boldsymbol{F}:\mathbb{R}^{m\times n}\to\mathbb R^{p\times q}$,我们同样可以利用向量化算子得到其 Jacobian 矩阵。我们分别将矩阵变元向量化:$\text{vec}(\boldsymbol{X})$、矩阵函数向量化:$\text{vec}(\boldsymbol{F}(\boldsymbol{X}))$,从而得到了一个 $\mathbb R^{mn}\times \mathbb R^{pq}$的变换,所以:
$$ \text{D}_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})=\frac{\partial \text{vec}(\boldsymbol{F}(\boldsymbol{X}))}{\partial \text{vec}^\top (\boldsymbol{X})}\in\mathbb{R}^{pq\times mn} $$
其具体形式为:
$$ \begin{bmatrix} \frac{\partial F_{11}(\boldsymbol{X})}{\partial x_{11}} & \cdots &\frac{\partial F_{11}(\boldsymbol{X})}{\partial x_{m1}} & \cdots &\frac{\partial F_{11}(\boldsymbol{X})}{\partial x_{1n}} &\cdots &\frac{\partial F_{11}(\boldsymbol{X})}{\partial x_{mn}}\\ \vdots & \ddots &\vdots & \ddots &\vdots & \ddots&\vdots\\ \frac{\partial F_{p1}(\boldsymbol{X})}{\partial x_{11}} & \cdots &\frac{\partial F_{p1}(\boldsymbol{X})}{\partial x_{m1}} & \cdots &\frac{\partial F_{p1}(\boldsymbol{X})}{\partial x_{1n}} &\cdots &\frac{\partial F_{p1}(\boldsymbol{X})}{\partial x_{mn}}\\ \vdots & \ddots &\vdots & \ddots &\vdots & \ddots&\vdots\\ \frac{\partial F_{1q}(\boldsymbol{X})}{\partial x_{11}} & \cdots &\frac{\partial F_{1q}(\boldsymbol{X})}{\partial x_{m1}} & \cdots &\frac{\partial F_{1q}(\boldsymbol{X})}{\partial x_{1n}} &\cdots &\frac{\partial F_{1q}(\boldsymbol{X})}{\partial x_{mn}}\\ \vdots & \ddots &\vdots & \ddots &\vdots & \ddots&\vdots\\ \frac{\partial F_{pq}(\boldsymbol{X})}{\partial x_{11}} & \cdots &\frac{\partial F_{pq}(\boldsymbol{X})}{\partial x_{m1}} & \cdots &\frac{\partial F_{pq}(\boldsymbol{X})}{\partial x_{1n}} &\cdots &\frac{\partial F_{pq}(\boldsymbol{X})}{\partial x_{mn}}\\ \end{bmatrix}_{pq\times mn} $$
(4)小结
现在,我们可以对三类函数、两种变元组合而成的六种情况下的 Jacobian 矩阵进行总结了:
| 函数 | Jacobian 矩阵定义 | 形状 |
|---|---|---|
| $f(\boldsymbol{x}):\mathbb{R}^m\to \mathbb{R}$ | $\frac{\partial f(\boldsymbol{x})}{\partial x^\top}$ | $\boldsymbol{J}\in\mathbb{R}^{1\times m}$ |
| $f(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}$ | $\frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}^\top}$ | $\boldsymbol{J}\in\mathbb{R}^{n\times m}$ |
| $\boldsymbol{f}(\boldsymbol{x}):\mathbb{R}^m\to\mathbb{R}^p$ | $\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial \boldsymbol{x}^\top}$ | $\boldsymbol{J}\in\mathbb{R}^{p\times m}$ |
| $\boldsymbol{f}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^p$ | $\frac{\partial \boldsymbol{f}(X)}{\partial \text{vec}^\top(\boldsymbol{X})}$ | $\boldsymbol{J}\in\mathbb{R}^{p\times mn}$ |
| $\boldsymbol{F}(\boldsymbol{x}):\mathbb{R}^{m}\to\mathbb{R}^{p\times q}$ | $\frac{\partial \text{vec}(\boldsymbol{F}(\boldsymbol{x}))}{\partial \boldsymbol{x}^\top}$ | $\boldsymbol{J}\in\mathbb{R}^{pq\times mn}$ |
| $\boldsymbol{F}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^{p\times q}$ | $\frac{\partial \text{vec}(\boldsymbol{F}(\boldsymbol{X}))}{\partial \text{vec}^\top(\boldsymbol{X})}$ | $\boldsymbol{J}\in\mathbb{R}^{pq\times mn}$ |
1.2:梯度矩阵
事实上,梯度算子 $\nabla$就是偏导算子 $\text{D}$的转置,相应的,梯度矩阵就是 Jacobian 矩阵的转置,但是实际中梯度矩阵更常用。
比如,对于向量变元的标量函数 $f:\mathbb{R}^m\to\mathbb{R}$,其偏导算子为 $\text{D}_{\boldsymbol{x}}=\left[\frac{\partial}{\partial x_1},\cdots,\frac{\partial}{\partial x_m}\right]$,而梯度算子为:
$$ \nabla_{\boldsymbol{x}}= \begin{bmatrix} \frac{\partial}{\partial x_1}\\ \vdots\\ \frac{\partial}{\partial x_m} \end{bmatrix} $$
回顾我们关于方向导数的论述,设有一方向 $\boldsymbol{u}$,该方向上的单位向量为 $\boldsymbol{e}_{\boldsymbol{u}}$,于是我们有:
$$ \frac{\partial f}{\partial \boldsymbol{u}}=\nabla_\boldsymbol{x} f\cdot \boldsymbol{e}_{\boldsymbol{u}} $$
所以,在 $\boldsymbol{x}$处,沿着 $\nabla_{\boldsymbol{x}}f(\boldsymbol{x})$方向函数以最大增大率增加;反之沿着负梯度方向则以最大减小率下降。
2、一阶实矩阵微分
在第一章中我们讨论了 Jacobian 矩阵也就是偏导,而偏导与微分是离不开的。并且对于比较复杂的函数如 $tr(\boldsymbol{X}),\det(\boldsymbol{X})$,求若干偏导数再组合起来比较困难,我们希望能有一种快速有效的 Jacobian 矩阵求解工具,这就是这一章要考虑的问题。
2.1:矩阵微分的定义及若干性质
(由于标量、向量都可以视作特殊的矩阵,因此下面我们就只关注矩阵的微分了。)
设有矩阵 $\boldsymbol{X}=(x_{ij})_{m\times n}$,则其微分定义为:$\text{d} \boldsymbol{X}=(\text{d} x_{ij})_{m\times n}$。它具有如下性质:
(1)线性:$\text{d}(\alpha\boldsymbol{X}+\beta\boldsymbol{Y})=\alpha\text{d}\boldsymbol{X}+\beta\text{d} \boldsymbol{Y}$
(2)转置:$\text{d}(\boldsymbol{X}^\top)=(\text d \boldsymbol{X})^\top$
(3)常数矩阵:$\boldsymbol{C}$是常数矩阵,则 $\text d \boldsymbol{C}=\boldsymbol{O}$
(4)矩阵乘积:$\text d (\boldsymbol{UV})=(\text{d} \boldsymbol{U})\boldsymbol{V}+\boldsymbol{U}\text d \boldsymbol{V}$,证明
注意这里都是矩阵,所以千万不能随便调换位置。结合性质(3)(4),有若 $\boldsymbol{C}$为常数矩阵,则 $\text d (\boldsymbol{CX})=\boldsymbol{C}\text d \boldsymbol{X}$
(5)矩阵和(差):$\text d (\boldsymbol{U}\pm\boldsymbol{V})=\text d \boldsymbol{U}\pm\text d \boldsymbol{V}$
(6)迹:$\text d (tr(\boldsymbol{X}))=tr(\text d \boldsymbol{X})$
(7)行列式:$\text d |\boldsymbol{X}|=|\boldsymbol{X}|tr(\boldsymbol{X}^{-1}\text d \boldsymbol{X})$,证明
(8)Hadamard 积:$\text d (\boldsymbol{U}\circ\boldsymbol{V})=(\text d \boldsymbol{U})\circ\boldsymbol{V}+\boldsymbol{U}\circ\text d \boldsymbol{V}$
(9)逆矩阵:$\text d (\boldsymbol{X}^{-1})=-\boldsymbol{X}^{-1}(\text d \boldsymbol{X})\boldsymbol{X}^{-1}$,证明
2.2:标量函数的 Jacobian 矩阵辨识与求解
回顾标量函数 Jacobian 矩阵的定义,
$$ \text d f(\boldsymbol{X})=\boldsymbol{J}\text d \boldsymbol{X}\tag{1} $$
对(1)式两边同时取迹,若 $f$为一标量函数即 $f=tr(f)$,则:
$$ \text d f(\boldsymbol{X})=tr(\boldsymbol{J}\text d \boldsymbol{X}) $$
由于 Jacobian 矩阵是唯一的,这启示我们:对于实值标量函数 $f$,若矩阵 $\boldsymbol{A}$满足 $\text d f(\boldsymbol{X})=tr(\boldsymbol{A}\text d \boldsymbol{X})$,则 $\boldsymbol{A}$就是 $f$在 $\boldsymbol{X}$处的 Jacobian 矩阵!至于说为什么要套一层 $tr$,一是可能让 $\boldsymbol{X}$保持矩阵的形式,二是 $tr$本身就是标量函数且在很多变换中具有不变性!这能给我们带来许多便利。
现在我们可以基于该定理与矩阵微分的性质来快速求解标量函数的 Jacobian 矩阵与梯度矩阵了。我们首先来看两个特殊的标量函数:迹与行列式。
(1)迹函数的梯度矩阵
例 1.求解 $tr(\boldsymbol{X}^\top\boldsymbol{X})$的梯度矩阵 $\frac{\partial tr(\boldsymbol{X}^\top\boldsymbol{X})}{\partial \boldsymbol{X}}$
法一:基于微分的视角
$$ \begin{align}\text d tr(\boldsymbol{X}^\top\boldsymbol{X})&=tr(\text d (\boldsymbol{X}^\top\boldsymbol{X}))\\ &=tr((\text d \boldsymbol{X}^\top)\boldsymbol{X})+tr(\boldsymbol{X}^\top\text d \boldsymbol{X})\\ &=tr(2\boldsymbol{X}^\top\text d \boldsymbol{X}) \end{align} $$
由标量函数 Jacobian 矩阵辨识定理立刻有 $\boldsymbol{J}=2\boldsymbol{X}^\top$,梯度矩阵则为 $2\boldsymbol{X}$。
法二:基于偏导的视角
求解梯度矩阵,我们也可以用原始的方法,即求解函数对每个元素的偏导再组合。我们知道,$tr(\boldsymbol{X}^\top\boldsymbol{X})=\sum\limits_{i=1}^m \sum\limits_{j=1}^n x_{ij}^2$,于是$\frac{\partial tr(\boldsymbol{X}^\top\boldsymbol{X})}{\partial x_{ij}}=2x_{ij}$,于是梯度矩阵$\frac{\partial tr(\boldsymbol{X}^\top\boldsymbol{X})}{\partial \boldsymbol{X}}=2\boldsymbol{X}$。
例 2.求解$tr(\boldsymbol{AX}^{-1})$ 的梯度矩阵,其中$\boldsymbol{A}$ 是常数矩阵
对于这个题而言,偏导的方法就不太好下手了,而从微分视角:
$$ \begin{align} \text d tr(\boldsymbol{AX}^{-1})&=tr(\boldsymbol{A}\text d \boldsymbol{X})\\ &=tr(-\boldsymbol{AX}^{-1}(\text d \boldsymbol{X})\boldsymbol{X}^{-1})\\ &=tr((\text d \boldsymbol{X})\boldsymbol{X}^{-1}\boldsymbol{AX}^{-1})\\&=tr(\boldsymbol{X}^{-1}\boldsymbol{AX}^{-1}\text d \boldsymbol{X}) \end{align} $$
所以,梯度矩阵为 $-(\boldsymbol{X}^{-1}\boldsymbol{AX}^{-1})^\top$
下图总结了常见的迹函数的微分矩阵与 Jacobian 矩阵:
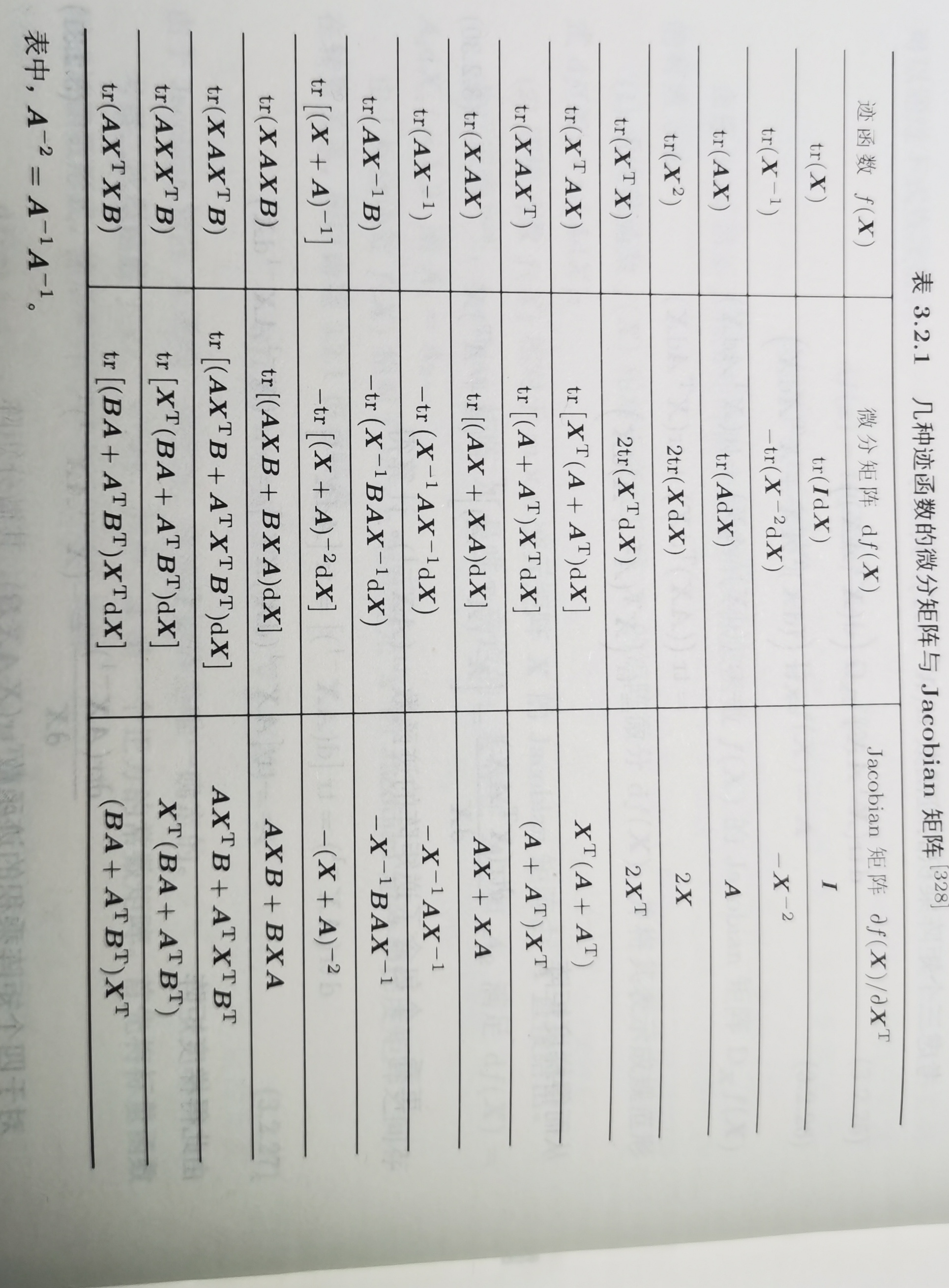
(2)行列式函数的梯度矩阵
例 1.求解 $|\boldsymbol{X}^k|$的梯度矩阵
由于 $|\boldsymbol{AB}|=|\boldsymbol{A}|\cdot |\boldsymbol{B}|$,所以:
$$ \begin{align}\text d (\boldsymbol{X}^k)&=\text d (|\boldsymbol{X}|)^k\\ &=k|\boldsymbol{X}|^{k-1}tr(|\boldsymbol{X}|\boldsymbol{X}^{-1}\text d \boldsymbol{X})\\ &=k|\boldsymbol{X}^k|tr(\boldsymbol{X}^{-1}\text d \boldsymbol{X}) \end{align} $$
所以梯度矩阵为 $k|\boldsymbol{X}^k|\boldsymbol{X}^{-\top}$
例 2.求解 $|\boldsymbol{X}^{-1}|$的梯度矩阵
$\boldsymbol{J}^\top=-|\boldsymbol{X}^{-1}|\boldsymbol{X}^{-\top}$,过程留做练习。
下图总结了常见的行列式函数的微分矩阵与 Jacobian 矩阵:
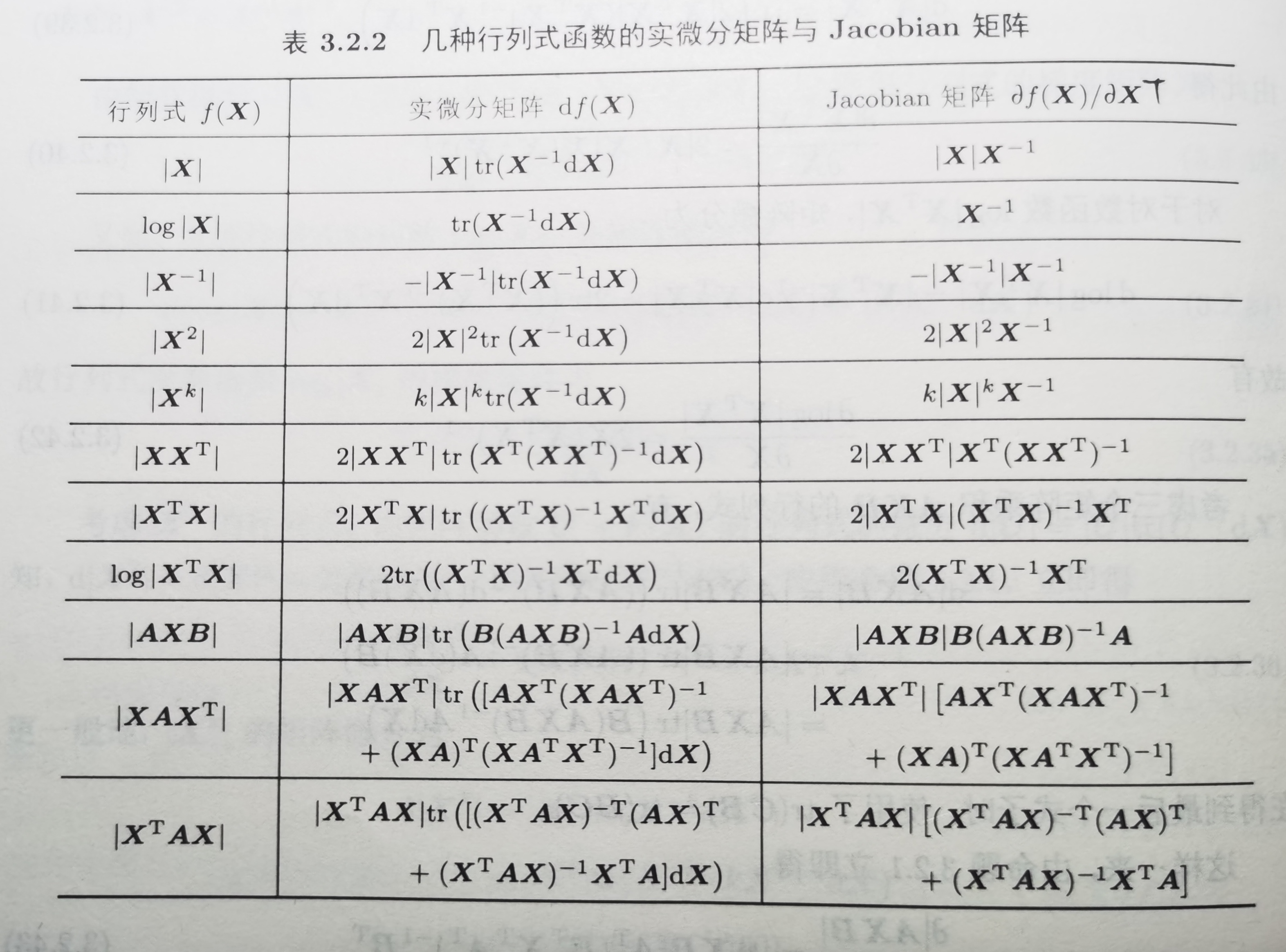
(3)其他例子
例 1.求解二次型函数 $\boldsymbol{x}^\top\boldsymbol{Ax}$的梯度矩阵,其中 $\boldsymbol{A}$为一常数方阵
法一:基于微分的视角
$$ \begin{align}\text d (\boldsymbol{x}^\top\boldsymbol{Ax})&=\text d tr(\boldsymbol{x}^\top\boldsymbol{A}x)\\ &=tr\left((\text d \boldsymbol{x})^\top \boldsymbol{Ax}+\boldsymbol{x}^\top\boldsymbol{A}\text d \boldsymbol{x}\right)\\ &=tr\left(\boldsymbol{x}^\top(\boldsymbol{A}+\boldsymbol{A}^\top)\text d \boldsymbol{x}\right) \end{align} $$
所以梯度矩阵 $\boldsymbol{J}^\top=(\boldsymbol{A}^\top+\boldsymbol{A})\boldsymbol{x}$
法二:基于偏导的方法
显而易见地,涉及到矩阵乘法时,偏导会变得极其复杂,这篇文章:矩阵求导公式的数学推导(矩阵求导——基础篇)的作者很有毅力地给出了过程:
$$ \begin{align} \frac{\partial( \pmb{x}^T \pmb{A}\pmb{x})}{\partial{\pmb{x}}} &= \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{\pmb{x}}} \\\\ &= \begin{bmatrix} \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{x_1}} \\ \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{x_2}} \\ \vdots \\ \frac{\partial(a_{11}x_1x_1+a_{12}x_1x_2+\cdots+a_{1n}x_1x_n \\ +a_{21}x_2x_1+a_{22}x_2x_2+\cdots+a_{2n}x_2x_n \\ + \cdots \\ +a_{n1}x_nx_1+a_{n2}x_nx_2+\cdots+a_{nn}x_nx_n)}{\partial{x_n}} \end{bmatrix} \\\\ &= \begin{bmatrix} (a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n)+(a_{11}x_1+a_{21}x_2+\cdots+a_{n1}x_n) \\ (a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n)+(a_{12}x_1+a_{22}x_2+\cdots+a_{n2}x_n) \\ \vdots \\ (a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n)+(a_{1n}x_1+a_{2n}x_2+\cdots+a_{nn}x_n) \end{bmatrix} \\\\ &= \begin{bmatrix} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n \\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n \\ \vdots \\ a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n \end{bmatrix} +\begin{bmatrix} a_{11}x_1+a_{21}x_2+\cdots+a_{n1}x_n \\ a_{12}x_1+a_{22}x_2+\cdots+a_{n2}x_n \\ \vdots \\ a_{1n}x_1+a_{2n}x_2+\cdots+a_{nn}x_n \end{bmatrix} \\\\ &= \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} +\begin{bmatrix} a_{11}&a_{21}&\cdots&a_{n1}\\ a_{12}&a_{22}&\cdots&a_{n2}\\ \vdots&\vdots&\ddots&\vdots\\ a_{1n}&a_{2n}&\cdots&a_{nn} \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} \\\\ &= \pmb{A}\pmb{x}+\pmb{A}^T \pmb{x} \end{align} $$
例 2.求解 $\boldsymbol{a}^\top\boldsymbol{xb}$的梯度矩阵
$\boldsymbol{J}^\top=\boldsymbol{ab}^\top$,留做练习。
2.3:向量函数的 Jacobian 矩阵辨识与求解
设有一向量函数:$\boldsymbol{f}(\boldsymbol{x}):\mathbb{R}^m\to\mathbb{R}^p$,则:
$$ \text{d}\boldsymbol{f}(\boldsymbol{x})= \begin{bmatrix} \text d f_1(\boldsymbol{x})\\ \vdots\\ \text d f_p(\boldsymbol{x}) \end{bmatrix}= \begin{bmatrix} \sum\limits_{i=1}^m \frac{\partial f_1(\boldsymbol{x})}{\partial x_{i}}\\ \vdots\\ \sum\limits_{i=1}^m \frac{\partial f_p(\boldsymbol{x})}{\partial x_{i}} \end{bmatrix} $$
同时注意到 $\boldsymbol{f}$在 $\boldsymbol{x}$处的 Jacobian 矩阵为:
$$ \boldsymbol{J}=\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial \boldsymbol{x}^\top}= \begin{bmatrix} \frac{\partial f_1(\boldsymbol{x})}{\partial x_1} & \cdots & \frac{\partial f_1(\boldsymbol{x})}{\partial x_m}\\ \vdots & \ddots & \vdots\\ \frac{\partial f_p(\boldsymbol{x})}{\partial x_1}&\cdots &\frac{\partial f_p(\boldsymbol{x})}{\partial x_m} \end{bmatrix} $$
于是立刻有:
$$ \text d \boldsymbol{f}(\boldsymbol{x})=\boldsymbol{J}\text d \boldsymbol{x} $$
类似地,对于 $\boldsymbol{f}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^p$,有:
$$ \text d \boldsymbol{f}(\boldsymbol{X})=\boldsymbol{J}\text d (\text{vec}(\boldsymbol{X})) $$
事实上,我们便得到了向量函数的 Jacobian 辨识:
$$ \begin{align} \text d \boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A}\text d \boldsymbol{x}\Leftrightarrow &\text D_{\boldsymbol{x}}\boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A}\\ \text d \boldsymbol{f}(\boldsymbol{X})=\boldsymbol{A}\text d (\text{vec}(\boldsymbol{X}))&\Leftrightarrow \text D_{\text {vec}\boldsymbol{X}}\boldsymbol{f}(\boldsymbol{X})=\boldsymbol{A} \end{align} $$
2.4:矩阵函数的 Jacobian 矩阵辨识与求解
对于更复杂的矩阵函数,我们又该如何快速辨识 Jacobian 矩阵呢?我们先看 $\boldsymbol{F}(\boldsymbol{x}):\mathbb{R}^{m}\to\mathbb{R}_{p\times q}$。
$$ \text{vec}(\text d \boldsymbol{F}(\boldsymbol{x}))=\text d (\text{vec}(\boldsymbol{F}(x)))= \begin{bmatrix} dF_{11}(\boldsymbol{x})\\ \vdots\\ dF_{p1}(\boldsymbol{x})\\ \vdots\\ dF_{1q}(\boldsymbol{x})\\ \vdots\\ dF_{pq}(\boldsymbol{x})\\ \end{bmatrix} =\begin{bmatrix} \sum_k^m \frac{\partial F_{11}(\boldsymbol{x})}{\partial x_k}\\ \vdots\\ \sum_k^m \frac{\partial F_{p1}(\boldsymbol{x})}{\partial x_k}\\ \vdots\\ \sum_k^m \frac{\partial F_{1q}(\boldsymbol{x})}{\partial x_k}\\ \vdots\\ \sum_k^m \frac{\partial F_{pq}(\boldsymbol{x})}{\partial x_k}\\ \end{bmatrix} $$
同时注意到 $\boldsymbol{F}(\boldsymbol{x})$在 $\boldsymbol{x}$处的 Jacobian 矩阵为:
$$ \boldsymbol{J}=\frac{\text{vec}(\boldsymbol{F}(\boldsymbol{x}))}{\partial \boldsymbol{x}^\top}= \begin{bmatrix} \frac{\partial F_{11}(\boldsymbol{X})}{\partial x_{1}} & \cdots &\frac{\partial F_{11}(\boldsymbol{X})}{\partial x_{m}} \\ \vdots & \ddots &\vdots \\ \frac{\partial F_{p1}(\boldsymbol{X})}{\partial x_{1}} & \cdots &\frac{\partial F_{p1}(\boldsymbol{X})}{\partial x_{m}}\\ \vdots & \ddots &\vdots \\ \frac{\partial F_{1q}(\boldsymbol{X})}{\partial x_{1}} & \cdots &\frac{\partial F_{1q}(\boldsymbol{X})}{\partial x_{m}}\\ \vdots & \ddots &\vdots \\ \frac{\partial F_{pq}(\boldsymbol{X})}{\partial x_{1}} & \cdots &\frac{\partial F_{pq}(\boldsymbol{X})}{\partial x_{m}}\\ \end{bmatrix}_{pq\times m} $$
所以:
$$ \text d(\text{vec}\boldsymbol{F}(\boldsymbol{x}))=\boldsymbol{J}\text d \boldsymbol{x} $$
推而广之,最复杂的 $\boldsymbol{F}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^{p\times q}$也容易得出:
$$ \text d(\text{vec}\boldsymbol{F}(\boldsymbol{X}))=\boldsymbol{J}\text d (\text{vec}\boldsymbol{X}) $$
2.5: 小结
现在,我们可以对三类函数、两种变元组合而成的六种情况下的 Jacobian 矩阵的定义与辨识进行总结了。结合定义表,我们有:
| 函数 | 定义 | 辨识 | 形状 |
|---|---|---|---|
| $f(\boldsymbol{x}):\mathbb{R}^m\to \mathbb{R}$ | $\frac{\partial f(\boldsymbol{x})}{\partial x^\top}$ | $\text d f(\boldsymbol{x})=tr(\boldsymbol{J}\text d \boldsymbol{x})$ | $\boldsymbol{J}\in\mathbb{R}^{1\times m}$ |
| $f(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}$ | $\frac{\partial f(\boldsymbol{X})}{\partial \boldsymbol{X}^\top}$ | $\text d f(\boldsymbol{X})=tr(\boldsymbol{J}\text d \boldsymbol{X})$ | $\boldsymbol{J}\in\mathbb{R}^{n\times m}$ |
| $\boldsymbol{f}(\boldsymbol{x}):\mathbb{R}^m\to\mathbb{R}^p$ | $\frac{\partial \boldsymbol{f}(\boldsymbol{x})}{\partial \boldsymbol{x}^\top}$ | $\text d \boldsymbol{f}(\boldsymbol{x})=\boldsymbol{J}\text d \boldsymbol{x}$ | $\boldsymbol{J}\in\mathbb{R}^{p\times m}$ |
| $\boldsymbol{f}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^p$ | $\frac{\partial \boldsymbol{f}(X)}{\partial \text{vec}^\top(\boldsymbol{X})}$ | $\text d \boldsymbol{f}(\boldsymbol{X})=\boldsymbol{J}\text d (\text{vec}(\boldsymbol{X}))$ | $\boldsymbol{J}\in\mathbb{R}^{p\times mn}$ |
| $\boldsymbol{F}(\boldsymbol{x}):\mathbb{R}^{m}\to\mathbb{R}^{p\times q}$ | $\frac{\partial \text{vec}(\boldsymbol{F}(\boldsymbol{x}))}{\partial \boldsymbol{x}^\top}$ | $\text d(\text{vec}\boldsymbol{F}(\boldsymbol{x}))=\boldsymbol{J}\text d \boldsymbol{x}$ | $\boldsymbol{J}\in\mathbb{R}^{pq\times mn}$ |
| $\boldsymbol{F}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^{p\times q}$ | $\frac{\partial \text{vec}(\boldsymbol{F}(\boldsymbol{X}))}{\partial \text{vec}^\top(\boldsymbol{X})}$ | $\text d(\text{vec}\boldsymbol{F}(\boldsymbol{X}))=\boldsymbol{J}\text d (\text{vec}\boldsymbol{X})$ | $\boldsymbol{J}\in\mathbb{R}^{pq\times mn}$ |
回过头来看本章的心路历程,我们从向量变元的标量函数 $f(\boldsymbol{x})$的偏导数处引入了 Jacobian 矩阵,而稍复杂函数的 Jacobian 矩阵我们直接给出了具体形式。而后由于基于定义求解 Jacobian 矩阵的复杂性我们引入了微分的视角,同时这又反过头来说明了 Jacobian 为什么有那样的形式。类似于一元函数微分学,这里的偏导与微分也是殊途同归的。
*2.6:矩阵函数 Jacobian 矩阵辨识的引申
上文我们讨论了矩阵函数 Jacobian 矩阵的辨识,并给出了初步结论。基于此,教材上给出了两个更加便于使用的结论。
对 $\boldsymbol{F}(\boldsymbol{X}),\boldsymbol{X}\in\mathbb{R}^{m\times n}$,其微分总可以表示成
$$ \text d (\text{vec}\boldsymbol{F}(\boldsymbol{X}))=\boldsymbol{A}\text d (\text{vec}\boldsymbol{X})+\boldsymbol{B}\text d (\text{vec}(\boldsymbol{X}^\top)) $$
由于 $\text d (\text{vec}(\boldsymbol{X}^\top))=\text{vec}(\text d (\boldsymbol{X}^\top))=\boldsymbol{K}_{mn}\text{vec}(\text d \boldsymbol{X})$,所以辨识定理可以写成:
$$ \text d (\text{vec}\boldsymbol{F}(\boldsymbol{X}))=\boldsymbol{A}\text d (\text{vec}\boldsymbol{X})+\boldsymbol{B}\text d (\text{vec}(\boldsymbol{X}^\top))\Leftrightarrow \text D_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})=\boldsymbol{A}+\boldsymbol{BK}_{mn} $$
同时注意到 $\text{vec}(\boldsymbol{ABC})=(\boldsymbol{C}^\top\otimes\boldsymbol{A})\text{vec}(\boldsymbol{B})$,所以如果 $\boldsymbol{F}(\boldsymbol{X})$的微分是 $\boldsymbol{A}(\text d \boldsymbol{X})\boldsymbol{B}$或 $\boldsymbol{A}(\text d \boldsymbol{X}^\top)\boldsymbol{B}$的形式,辨识定理还可以写成:
$$ \text d \boldsymbol{F}(\boldsymbol{X})=\boldsymbol{A}(\text d \boldsymbol{X})\boldsymbol{B}+\boldsymbol{C}(\text d \boldsymbol{X}^\top)\boldsymbol{D}\Leftrightarrow \text D_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})=(\boldsymbol{B}\otimes\boldsymbol{A}^\top)+\boldsymbol{K}_{nm}(\boldsymbol{D}\otimes \boldsymbol{C}^\top) $$
练习:试求 $\text D_{\boldsymbol{X}}\boldsymbol{X}\otimes \boldsymbol{Y}$。
3、Hessian 矩阵
在讨论完一阶偏导后,下一部分自然是二阶偏导。类似地,我们以偏导视角给出 Hessian 矩阵的定义,并从微分视角讨论它的辨识。为了简便考虑,以下就只关注标量函数 $f(\boldsymbol{x}),f(\boldsymbol{X})$了。
实值标量函数 $f(\boldsymbol{x})$相对于 $m\times 1$的向量变元 $\boldsymbol{x}$的二阶偏导组成的矩阵称为 Hessian 矩阵,记为 $\boldsymbol{H}[f(\boldsymbol{x})]$,定义为:
$$ \boldsymbol{H}[f(\boldsymbol{x})]{\overset {\underset {\mathrm {def} }{}}{=}}\frac{\partial^2 f(\boldsymbol{x})}{\partial\boldsymbol{x}\partial \boldsymbol{x}^\top}\in\mathbb{R}^{m\times m} $$
如果我们考虑梯度算子 $\nabla_{\boldsymbol{x}}$与偏导算子 $\text{D}_{\boldsymbol{x}}$,则 Hessian 矩阵也可以写为:
$$ \boldsymbol{H}[f(\boldsymbol{x})]=\nabla^2_\boldsymbol{x}f(\boldsymbol{x})=\nabla_\boldsymbol{x}(\text D_{\boldsymbol{x}} f(\boldsymbol{x})) $$
具体地,Hessian 矩阵的元素为:
$$ \boldsymbol{H}[f(\boldsymbol{x})]= \begin{bmatrix} \frac{\partial^2 f}{\partial x_1\partial x_1}& \cdots&\frac{\partial^2 f}{\partial x_1\partial x_m}\\ \vdots & \ddots & \vdots\\ \frac{\partial^2 f}{\partial x_m\partial x_1}&\cdots&\frac{\partial^2 f}{\partial x_m\partial x_m} \end{bmatrix} $$
由于二阶导与求导顺序无关,即$\frac{\partial^2 f}{\partial x_i\partial x_j}=\frac{\partial^2 f}{\partial x_j\partial x_i}$,所以 Hessian 矩阵是对称的。
类似地,我们可以定义矩阵变元的标量函数的 Hessian 矩阵:
$$ \boldsymbol{H}[f(\boldsymbol{X})]{\overset {\underset {\mathrm {def} }{}}{=}}\frac{\partial^2 f(\boldsymbol{X})}{\partial \text{vec}\boldsymbol{X}\partial \text{vec}^\top\boldsymbol{X}}\in\mathbb{R}^{mn\times mn} $$
具体地:
$$ \boldsymbol{H}[f(\boldsymbol{X})]= \begin{bmatrix} \frac{\partial^2 f}{\partial x_{11}\partial x_{11}}&\cdots&\frac{\partial^2 f}{\partial x_{11}\partial x_{m1}}&\cdots&\frac{\partial^2 f}{\partial x_{11}\partial x_{1n}}&\cdots&\frac{\partial^2 f}{\partial x_{11}\partial x_{mn}}\\ \vdots&\ddots&\vdots&\ddots&\vdots&\ddots&\vdots\\ \frac{\partial^2 f}{\partial x_{m1}\partial x_{11}}&\cdots&\frac{\partial^2 f}{\partial x_{m1}\partial x_{m1}}&\cdots&\frac{\partial^2 f}{\partial x_{m1}\partial x_{1n}}&\cdots&\frac{\partial^2 f}{\partial x_{m1}\partial x_{mn}}\\ \vdots&\ddots&\vdots&\ddots&\vdots&\ddots&\vdots\\ \frac{\partial^2 f}{\partial x_{1n}\partial x_{11}}&\cdots&\frac{\partial^2 f}{\partial x_{1n}\partial x_{m1}}&\cdots&\frac{\partial^2 f}{\partial x_{1n}\partial x_{1n}}&\cdots&\frac{\partial^2 f}{\partial x_{1n}\partial x_{mn}}\\ \vdots&\ddots&\vdots&\ddots&\vdots&\ddots&\vdots\\ \frac{\partial^2 f}{\partial x_{mn}\partial x_{11}}&\cdots&\frac{\partial^2 f}{\partial x_{mn}\partial x_{m1}}&\cdots&\frac{\partial^2 f}{\partial x_{mn}\partial x_{1n}}&\cdots&\frac{\partial^2 f}{\partial x_{mn}\partial x_{mn}} \end{bmatrix}_{mn\times mn} $$
4、二阶实矩阵微分
我们分两种情况讨论 Hessian 矩阵的辨识。
4.1:向量变元:$f(\boldsymbol{x})$
注意到$\text d \boldsymbol{x}=[\text d x_1,\cdots,\text d x_m]^\top$并不是$\boldsymbol{x}$的函数,因此$\text d (\text d \boldsymbol{x})=0$。回顾一阶全微分的情况:
$$ \text d f(\boldsymbol{x})=\underbrace{\frac{\partial f(x)}{\partial \boldsymbol{x}^\top}}_{\boldsymbol{J}} \text d \boldsymbol{x}=(\text d \boldsymbol{x})^\top\frac{\partial f(x)}{\partial \boldsymbol{x}} $$
现在考察$\text{d}^2 f(\boldsymbol{x})$:
$$ \begin{align} \text{d}^2f(\boldsymbol{x})&=\text d(\text d f(\boldsymbol{x}))=(\text d \boldsymbol{x})^\top\frac{\partial \text d f(\boldsymbol{x})}{\partial \boldsymbol{x}}\\ &=(\text d \boldsymbol{x})^\top\left[\frac{\partial}{\partial \boldsymbol{x}}\left(\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}^\top}\right)\text d \boldsymbol{x}+\frac{\partial f(\boldsymbol{x})}{\partial\boldsymbol{x}^\top}\cdot\underbrace{\frac{\partial \text d \boldsymbol{x}}{\partial \boldsymbol{x}}}_{=0} \right]\\ &=(\text d \boldsymbol{x})^\top\frac{\partial^2 f(\boldsymbol{x})}{\partial \boldsymbol{x}\partial \boldsymbol{x}^\top}\text d \boldsymbol{x}=(\text d \boldsymbol{x})^\top \boldsymbol{H}[f(\boldsymbol{x})]\text d \boldsymbol{x} \end{align} $$
考虑到 Hessian 矩阵是对称的,所以我们可以如下辨识:
$$ \text d^2f(\boldsymbol{x})=(\text d \boldsymbol{x})^\top\boldsymbol{A}\text d \boldsymbol{x}\Leftrightarrow\boldsymbol{H}[f(\boldsymbol{x})]=\frac{1}{2}(\boldsymbol{A}+\boldsymbol{A}^\top) $$
4.2:矩阵变元:$f(\boldsymbol{X})$
如果我们将变元$\boldsymbol{X}$向量化:$\text{vec}\boldsymbol{X}\in\mathbb{R}^{mn\times 1}$,则我们可以作类似的分析:
$$ \begin{align} \text d^2f(\boldsymbol{X})&=(\text d \text{vec}\boldsymbol{X})^\top\left(\frac{\partial \text d f(\boldsymbol{X})}{\partial \text d \text{vec}\boldsymbol{X}}\right)\\ &=(\text d \text{vec}\boldsymbol{X})^\top\boldsymbol{H}[f(\boldsymbol{X})]\text d \text{vec}\boldsymbol{X} \end{align} $$
所以也有如下辨识:
$$ \text d^2f(\boldsymbol{X})=( \text d \text{vec}\boldsymbol{X})^\top\boldsymbol{A}\text d \text{vec}\boldsymbol{X}\Leftrightarrow\boldsymbol{H}[f(\boldsymbol{x})]=\frac{1}{2}(\boldsymbol{A}+\boldsymbol{A}^\top) $$
后记
至此,关于矩阵微分最基础的东西就介绍完了,至于说向量函数、矩阵函数的 Hessian 矩阵与辨识,还有后面的复矩阵微分分析这里就不展开了。
