前言

  本文介绍无需VQ的自回归图像生成工作MAR（masked autoregressive）。纵观整个视觉自回归，最普适最广泛的框架即是VQVAE离散化+transformer自回归生成，也由此才有RQ、LFQ、BSQ等tokenizer改进；而在此框架下也诞生了VQGAN、DALL-E、MAGVIT等经典工作。

经典自回归框架，以T2I为例，图源2

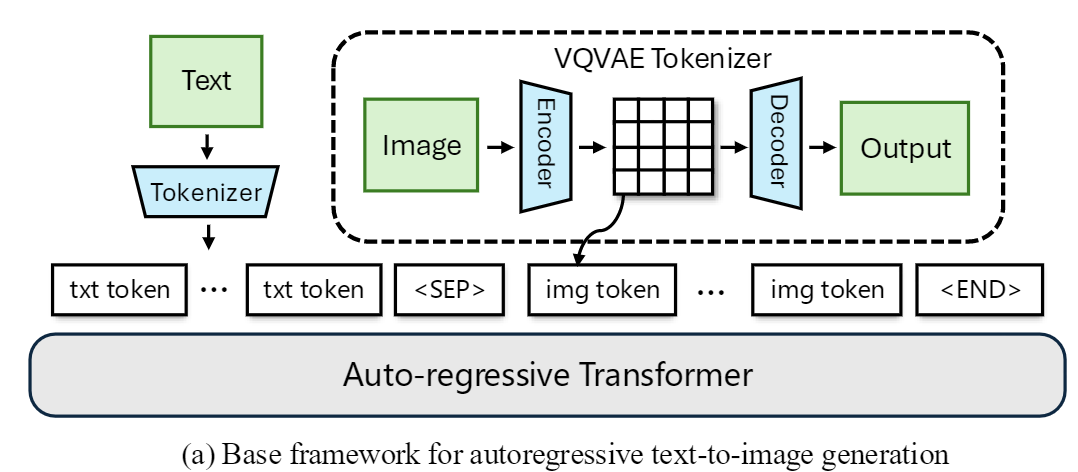
  不过我们如果重新审视VQ操作，其最主要的目的其实还是NLP是这样的且做成了，但是image其实天然是连续的，而且codebook也会带来一堆问题（重建误差、训练困难、词表坍缩等等），有没有可能跳出这个框架呢？
  在本质上生成可以视作一个采样过程，最常用的workflow即VQ离散化+交叉熵优化+top-K/P采样相当于从一个categorical的分布中采样，如果没有VQ，直接输出连续值+MSE并不是个分布，所以我们需要一种在连续空间建模每个像素概率分布的手段。
  同时传统的自回归生成时采用的通常是raster-order的生成顺序，即从上到下、从左至右进行扫描式的生成，显然这种方式会带来相当程度的bias。有没有更优雅的生成方式呢？带着这些问题，我们来看Kaiming带队的这篇MAR。

用扩散模型建模分布

  在之前的介绍中，我们回顾了VQ视觉自回归的心路历程，其中用到了很多通常、一般，说明逻辑推理是不严谨的，那自然地MAR作者提出了疑问：

Is it necessary for autoregressive models to be coupled with vector-quantized representations?

  我们回顾自回归的本质含义，即是用已知预测未知。在文本自回归生成中，输入是已生成文本，输出是下一个词的类别分布；而在图像自回归生成中，输入是已生成像素，输出是下一个像素的分布。

  作者从扩散模型中得到启发，现在扩散模型的大行其道不正是因为它可以根据任何信息如文本、类比等建模条件分布$p(x|z)$从而生成嘛？放到自回归生成的框架中是不是可以将之前生成的像素作为控制条件从而得到下一个像素的条件分布？就像下图这样：

用扩散模型建模下一个像素的分布，图源3

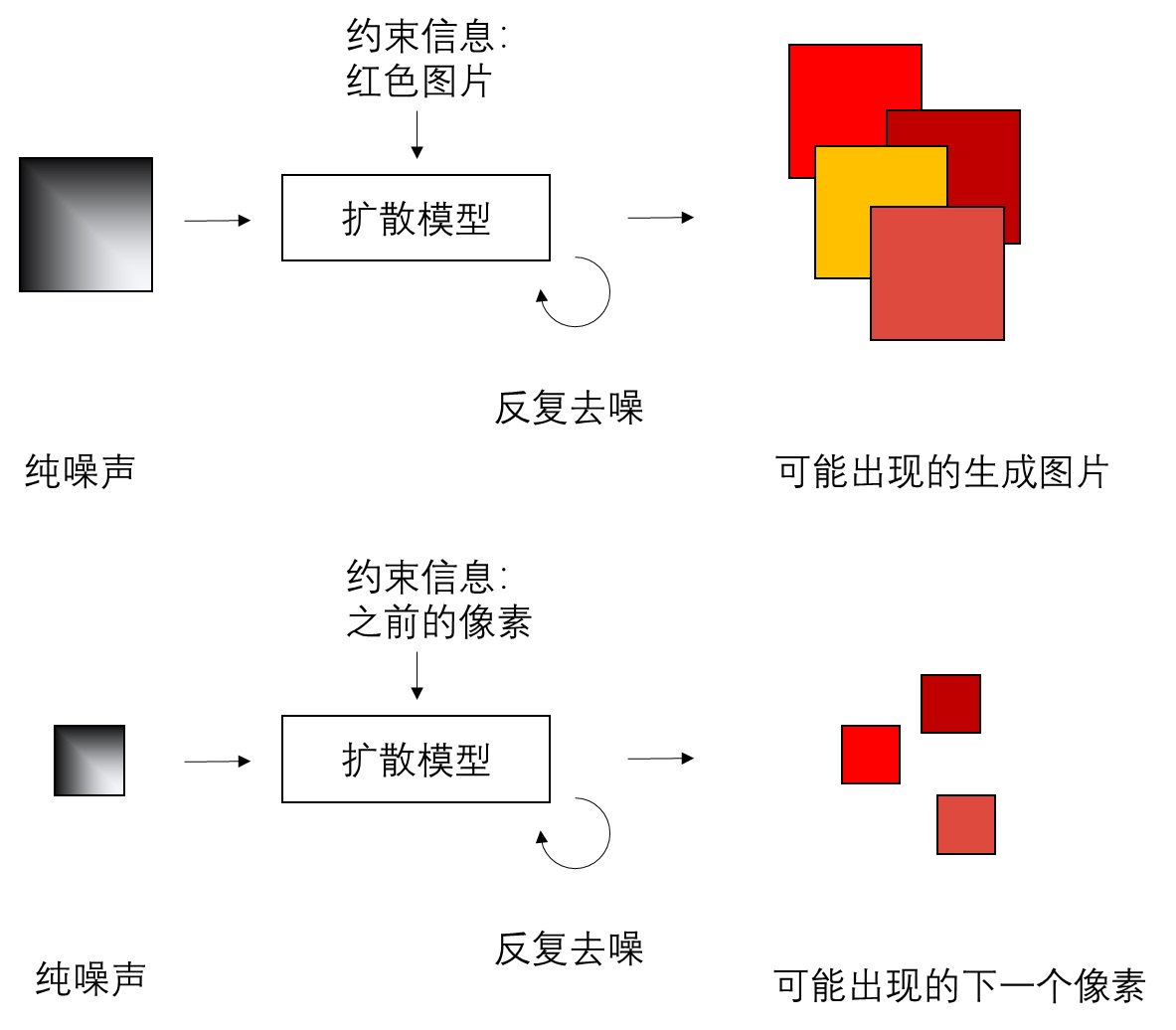
  当然与通常扩散模型建模图像分布不同，在那里是等价于要建模所有像素的联合分布，而在此处则是变为建模每个像素的分布。原话是：

in our case, the diffusion model is for representing the distribution for each token.

  对于形如：

$$ p(x_1,\cdots,x_n)=\prod_{i=1}^n p(x_i|x_1,\cdots,x_{i-1}) $$

的自适应生成，设已生成的token为$x_1,\cdots,x_{i-1}$，首先通过transformer得到一个条件变量$z_i=f_{\theta}(x_1,\cdots,x_{i-1})$；而后用diffusion建模条件概率$p(x_i|z_i)$，则参考DDPM有loss：

$$ \mathcal L(z_i,x_i)=\mathbb E_{\epsilon,t}\Big[\Vert \epsilon-\epsilon_{\theta'}(x_{i,t}|t,z_i) \Vert_2^2\Big] $$

其中$\epsilon\sim\mathcal N(0,1)$， $x_{i,t}$就是在时间步$t$下$x_i$的noised latent：$x_{i,t}=\sqrt{\beta_t}x_i+\sqrt{1-\beta_t}\cdot \epsilon$。而且这个loss的梯度不仅会更新扩散模型$\theta'$，还能传给transformer$\theta$。某种程度上，可以认为这个diffusion loss相当于原来的分类MLP+softmax+交叉熵的功能。

  由于这里diffusion只需要关注noise+$z_i$到$x_i$的过程，token之间的关联已经在transformer中体现了，所以也不需要attention，MAR直接用了3个由LayerNorm、MLP、SiLU、MLP组合的FFN。同时前缀约束信息$z$和降噪步数$t$按照DiT的AdaLN加入进去。

Next Set-of-tokens Prediction

  上文中我们解决了第一个问题，即如何在连续型分布中训练与采样。如果把这个diffusion loss套在常规的自回归上也已经可以生成了。不过作者进一步回答了我们的第二个问题：token之间的生成顺序是什么？

  其实正如作者所述，最贴近自回归本身意义的，应该仅仅是“基于已知的去预测未知的”，而“从上到下、从左至右”和“每次只预测一个token”其实既非充分也非必要条件。因为对于文本而言，先天地具有顺序关系；而像素之间并没有明确的顺序规定，所以更合理的视觉自回归生成方式应该像下图的(b)一样。同时为了加速，我们可以一次性预测一批token，即：next set-of-tokens prediction。

不同的自回归生成方式

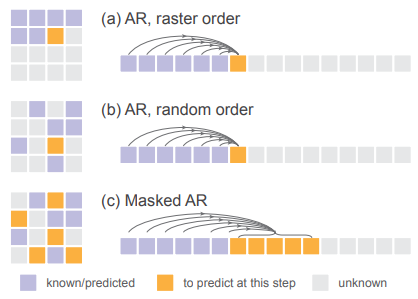
  同时还有一点值得注意，由于我们的生成粒度变为了set，而且需要将之前生成的set提取前缀信息$z_i$，其实对于需要生成的$x_i$是天然不存在train-test的gap的，所以作者自然地使用双向注意力机制来提取$z_i$，如下图：

MAR使用双向注意力提取前缀信息

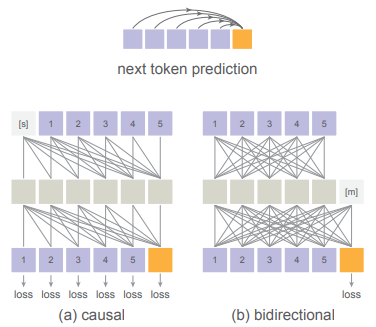
  最后是如何选择set-of-tokens。作者结合了MAE的做法——基于未mask的tokens去预测masked tokens中随机挑选的一个set；新预测的这批 tokens的mask被放开(成为unmasked tokens)，它们与之前的unmasked tokens 再一起去预测剩下的masked tokens中随机挑选的一批。就这样随着自回归的进行，masked的token越来越少直至得到全图。

一些细节

  前面我们梳理了一下MAR的整体流程，下面我们补充一些比较重要的细节。首先和绝大多数视觉自回归工作一样，生成过程是在AE的latent空间中完成的，具体用的是LDM的KL-VAE，将$[B,C,H,W]$的RGB图像进行$\times 16$倍的压缩$[B,c,h=\frac{H}{16},w=\frac W{16}]$。而后类似ViT分patch并reshape得到$[B,l=\lfloor\frac h p\rfloor\cdot\lfloor\frac wp\rfloor,d=cp^2]$，实际上$p=1$。划分后的每个patch加上位置编码后被视作token。同时在序列开头会有一个[cls]以便输入类别。

  在训练MAR时，首先设置一个最小的mask ratio(通常是 70%)，而后从一个截尾正态分布中采样一个mask比例。代码为：

self.mask_ratio_generator = scipy.stats.truncnorm((mask_ratio_min - 1.0) / 0.25, 0, loc=1.0, scale=0.25)

def sample_orders(self, bsz):
        # generate a batch of random generation orders
        orders = []
        for _ in range(bsz):
            order = np.array(list(range(self.seq_len)))
            np.random.shuffle(order)
            orders.append(order)
        orders = torch.Tensor(np.array(orders)).cuda().long()
        
        return orders

    def random_masking(self, x, orders):
        # generate token mask
        bsz, seq_len, _ = x.shape
        mask_rate = self.mask_ratio_generator.rvs(1)[0]  # 0.7~1.0
        num_masked_tokens = int(np.ceil(seq_len * mask_rate))
        mask = torch.zeros(bsz, seq_len, device=x.device)
        # 因 orders是随机的, 所以将需要mask的token数量掩盖掉即实现了随机 mask的效果
        mask = torch.scatter(mask, dim=-1, index=orders[:, :num_masked_tokens],
                             src=torch.ones(bsz, seq_len, device=x.device))
        
        return mask

  由于mask的比例比较大，所以训练时的序列长度可能很短，作者就在序列的开头补上64个[cls] (也要加上位置编码)。其余设计都与MAE相同。

  对于训练的diffusion loss，真正需要计算梯度的仅仅是masked tokens那部分的loss，只需将计算出来的loss tensor对应乘上mask再mean即可，因为loss tensor和$x,z$形状是相同的。

  接下来我们研究推理过程。首先我们需要设置自回归的步数（类似VAR中scale的数量），文中使用了64步。而后根据步数定义一种mask策略，使得 mask 比例随步数增加而减少，从100%开始逐渐下降，文中是cosine schedule。再根据当前的mask ratio设置好表示当前所有masked token的mask；以及表示下一轮迭代时所有masked token的mask_next。而mask-mask_next就表示本轮需要生成的tokens的位置。

def mask_by_order(mask_len, order, bsz, seq_len):
    masking = torch.zeros(bsz, seq_len).cuda()
    masking = torch.scatter(masking, dim=-1, index=order[:, :mask_len.long()], src=torch.ones(bsz, seq_len).cuda()).bool()
    return masking

# 自回归步数循环
for step in indices:
    # mask比例的余弦调度
    # mask ratio for the next round, following MaskGIT and MAGE.
    mask_ratio = np.cos(math.pi / 2. * (step + 1) / num_iter)
    # 根据 mask 比例和序列长度计算需要被 mask 掉的 token 数量
    mask_len = torch.Tensor([np.floor(self.seq_len * mask_ratio)]).cuda()

    # masks out at least one for the next iteration
    mask_len = torch.maximum(torch.Tensor([1]).cuda(),
 torch.minimum(torch.sum(mask, dim=-1, keepdims=True) - 1, mask_len))

    ''' get masking for next iteration and locations to be predicted in this iteration '''

    # 设置下一轮 masked tokens 的位置
    mask_next = mask_by_order(mask_len[0], orders, bsz, self.seq_len)

    # 计算本轮需要预测的 tokens 对应在序列的哪些位置
    if step >= num_iter - 1:
        # 若本轮是最后一轮, 则需要预测的 tokens 位置就是之前 mask 掉的所有位置
        mask_to_pred = mask[:bsz].bool()
    else:
        # 本轮是 masked(=True) 但下一轮是 unmasked(=False) 的位置即为本轮需要预测的 tokens 位置，使用 XOR(亦或)操作即可实现
        mask_to_pred = torch.logical_xor(mask[:bsz].bool(), mask_next.bool())

    # CFG 需要多复制一倍样本
    if not cfg == 1.0:
        mask_to_pred = torch.cat([mask_to_pred, mask_to_pred], dim=0)

    mask = mask_next

  显然我们从代码可以知道，生成tokens的顺序由shuffled的序列orders指定，直接按order为索引构建mask即可，不会出现mask=False而mask_next=True的情况。其余细节这里就不介绍了。

实验结果

1. 消融实验

  首先是diffusion loss、双向注意力和随机mask生成的优势。实验结果如下：

消融实验

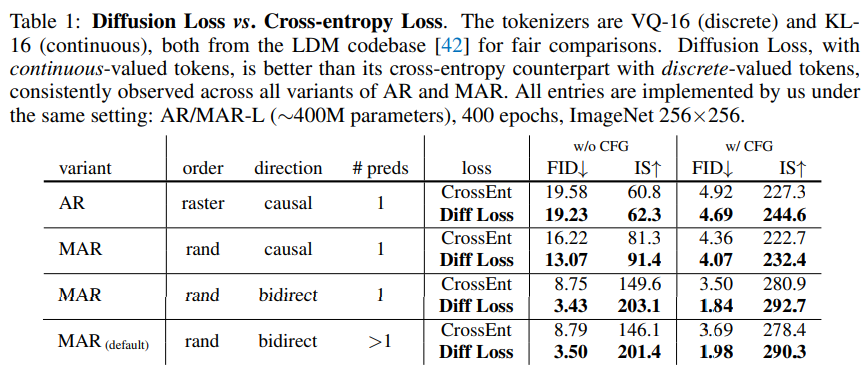
其中preds指每次生成的token数量。首先第一行diffusion loss对经典自回归框架的提升不明显，而将注意力从causal换成双向后提升显著，说明前缀约束信息$z_i$的提取效果对后续的降噪生成影响明显。而第四行相比第三行提升了每次预测的词元数，速度有提升但效果接近，因此后续实验都是基于第四行的配置。

2. SOTA指标对比

  以下是在ImageNet上$256\times256$的生成结果，还是有一定竞争力的。

图像生成指标与其他模型的对比

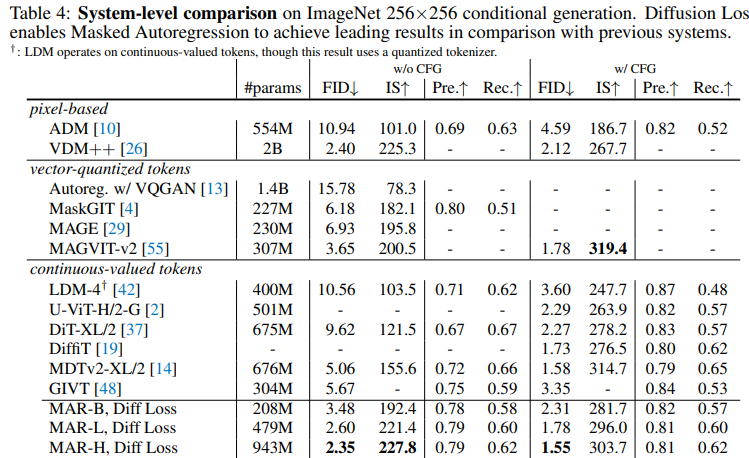
3. 生成效率

  文中同时展示了和DiT的对比结果。DiT的采样步数分别为(50 ,75, 150, 250)。而MAR展示的不同采样步数由自回归步数决定，分别为：(8, 16, 32, 64, 128)。DiT 最快也是一秒2.5张图像左右，而MAR默认设置（自回归步数 64）可以做到一秒生成3张图左右。

生成效率结果展示

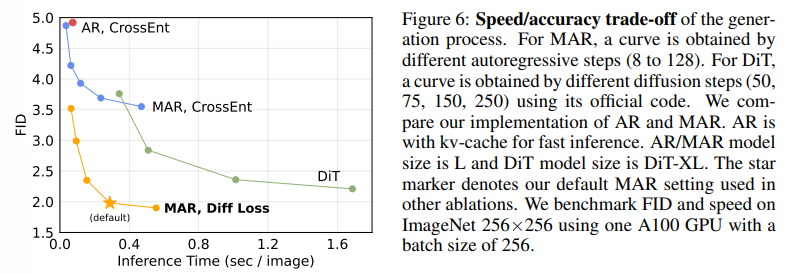
  不过由于MAR用的是双向注意力，所以不能用kv-cache加速推理，和最新的一些工作比在速度上优势并不明显。

总结

  总体看下来，MAR还是很高屋建瓴的，从建模all token分布的diffusion过程进行解耦拆解：用bidirection transformer建模前缀token之间的关系$z$；将$z$作为条件用超轻量的diffusion建模下一组token的分布，使得整体的复杂度大大降低。

  在学术上最大的takeaway便是回归了本质：

... autoregressive nature, i.e., “predicting next tokens based on previous ones”.

References

  1. Autoregressive Image Generation without Vector Quantization, NIPS 2024 (Spotlight) - MAR
    Tianhong Li, Yonglong Tian, He Li, Mingyang Deng, Kaiming He, 2024.06 | [[arXiv PDF]](https://arxiv.org/pdf/2406.11838)
  2. Autoregressive Models in Vision: A Survey, arXiv 24.11
    Jing Xiong et al., 2024.11 | [[arXiv PDF]](https://arxiv.org/pdf/2411.05902)
  3. 解读何恺明新作：不用向量离散化的自回归图像生成（Autoregressive Image Generation without Vector Quantization）
  4. MAR(Masked AutoRegressive): 破除封建迷信——谁说自回归图像生成一定需要 VQ(Vector Quantization) 的！
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏