VAR系列改进 (一)：缓解误差累积的Infinity

前言

  本文我们来看VAR原班人马出品的文生图工作Infinity。前脚VAR刚拿到NIPS的最佳论文，后脚Infinity就放出来了。训练、推理都已经开源，官网链接：https://foundationvision.github.io/infinity.project/。

  从论文中的图像来看还是非常不错的：

不论是写实感、人物细节还是文本表现都不错。而且作为文生图工作，文本的遵循能力也很好：

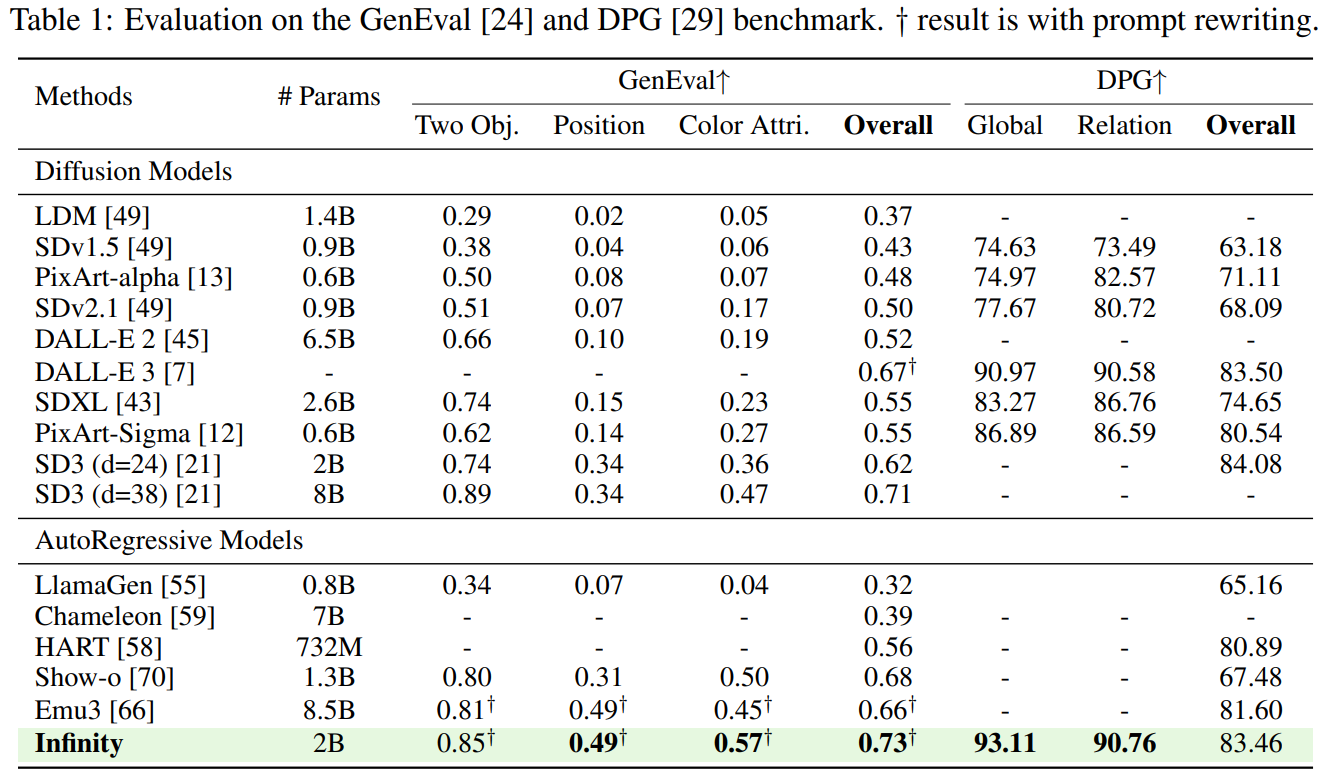
  从指标上来看，Infinity也确实达到了自回归T2I的SOTA，对比扩散模型也和SD3-M有一战之力。而且据论文所述生成一张1024×1024图像只需要0.8 s，比SD3-M快2.6倍，不过笔者没有实测过，不知道next-scale生成带来的的提升，还是有一些trivial的工程优化。目前只发布了2B模型，看github的开源计划后续还会发布20B的checkpoint，值得期待。接下来我们来详细看一下技术细节。

  Infinity的出发点其实老生常谈了：自回归中teacher-forcing导致的训练-推理gap、以及在大规模训练中扩大codebook大小导致的坍缩。我们还是从tokenize和generation两阶段来看具体做法。

Tokenize

  回顾VAR，它在量化尺度之间的“残差”时用的还是传统的lookup VQ，我们在：

中就提到这在大规模训练使用大codebook时会导致坍缩问题，那么自然地会想到使用lookup-free的量化方法如LFQ、BSQ等。具体到VAR的框架中，对于某个scale下需量化的feature$z_k\in\mathbb R^{h_k\times w_k\times d}$，逐位二值量化：

$$ q_{k,ij}=\begin{cases} \text{sign} (z_{k,ij}) & if\ use\ \text{LFQ} \\ \frac 1{\sqrt d}\text{sign} (z_{k,ij}) & if\ use\ \text{BSQ} \end{cases} $$

得到量化后的tokens：$q_k=[q_{k,ij}]_{h_k\times w_k}$。

  这里有个细节，LFQ在训练时需要一个熵惩罚loss：

$$ \mathcal L_{entropy}=\mathbb E[H(z_q)]-H(\mathbb E[z_q]) $$

在计算$z_q$的分布时，需要将$z\in\mathbb R^{B\times d}$和codebook的index矩阵$C\in \{1,-1\}^{2^d\times d}$做点积，具体当$d=2$时，C为：

$$ \begin{bmatrix} -1,&-1\\ -1,&1\\ 1,&1\\ 1,&1 \end{bmatrix}_{4\times 2} $$

则$dist(z_q)=softmax(zC^\top)\in\mathbb R^{B\times 2^d}$，空间复杂度是$O(2^d)$，那么显然在$d$极端大的时候可能会OOM。而使用BSQ则可以将空间复杂度降至在$O(d)$，从而使得在codebook很大时也不会OOM。

待补

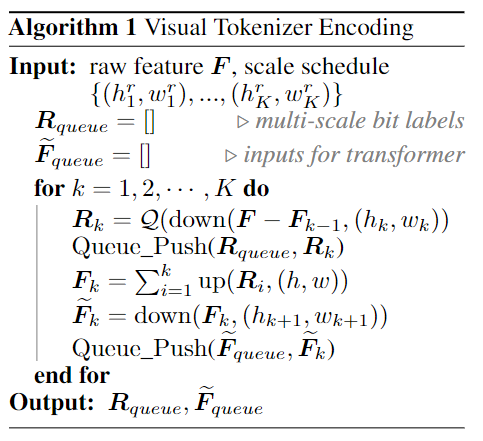
  总体而言的量化过程如下，看流程图还是比较清晰的：

Generation

  接下来我们来看Infinity的生成过程。在tokenize阶段我们成功将codebook扩展至了$V=2^{32}$乃至$V=2^{64}$，这在提升重建效果的同时也会带来一个严重问题，就是transformer最后的分类头会非常大！在transformer最后一层，我们需要从$h$维度的hidden states得到codebook的概率分布而后用交叉熵计算loss，这个线性层需要的时空复杂度为$O(h\times V+V)$，在$d=32,h=2048$时需要的显存将达8.8T！显然这种直接用线性层做分类头的方式不可取。

  Infinity的变动在于将$V$分类转换为了$d$个二分类：既然最后的token index是由$d$个量化index加权求和而成的，那用最终的token index作为GT其实没有太大的意义，到不如分解为$d$个$\{1,-1\}$二分类，这样就将过大的分类层$\boldsymbol W\in\mathbb R^{h\times 2^d}$分解为了$d$个分类层$\boldsymbol W\in\mathbb R^{h\times 2}$，这种做法文中称为Infinite-Vocabulary Classifier (IVC)。

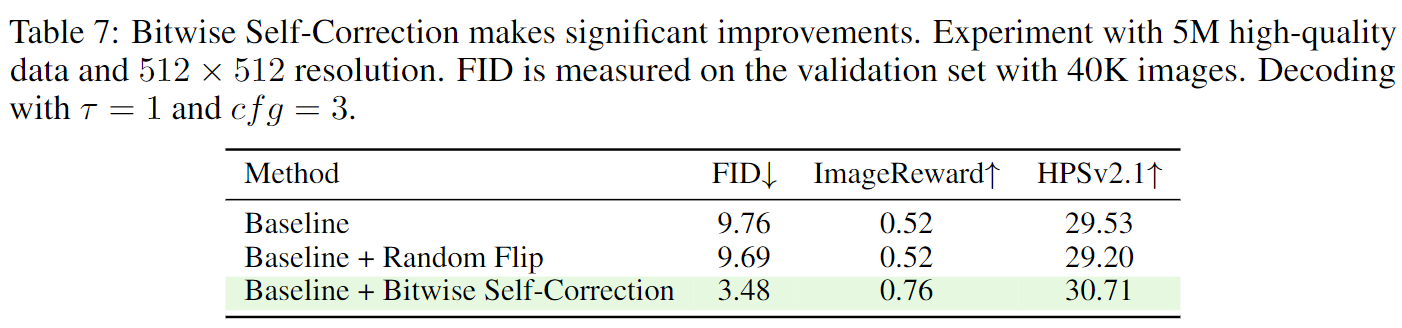
  同时这样做还有一个好处，使用二值量化的tokenizer对0附近的微小扰动是不鲁棒的，例如对于$d=4$，两个非常接近的未量化feature：$[1,-1,-2,0.1]$与$[1,-1,-2,-0.01]$在量化后的index分别为9（1+0+0+8）和1（1+0+0+0），用传统的token index作为GT优化会将这两个值显著分隔开；而用IVC则虽然最后一位上仍然会有不同的loss，但在前三位上的loss是一致的，从优化的角度也确保了这两者相对接近。从下表的结果来看，IVC不论是复杂度还是效果上都是显著超过传统做法的。

  Infinity在生成阶段的第二个重要改进是针对teacher-forcing的Bitwise Self-Correction (BSC)。对于所有自回归框架而言，推理时第${t}$步的输入为模型生成的前缀序列${\hat{\boldsymbol x}_{1:(t-1)}}$ 。而在训练时，我们使用的前缀序列是训练集中的真实数据${\boldsymbol{x}_{1:(t-1)}}$，这种学习方式称为Teacher Forcing。而显然由于模型分布和真实数据分布并不严格一致，因此存在协变量偏移问题，一旦在预测前缀 ${\hat{x}_{1:(t-1)}}$ 的过程中存在错误，会导致误差累计，使得后续生成的序列也会偏离真实分布，这个问题称为Exposure Bias。

  在NLP中，由于每个token都代表一个词/子词，所以可以调整采样方法来减少影响；而在VAR的框架中，由于并没有将完整图像拆解成内容相同、不同分辨率的词元图，而是拆解成了最低分辨率的图以及各个尺度上的信息损失，所以在生成最大尺度的残差$R_k$前无法进行loss计算以及优化。这导致scale-wise的自回归的误差累积非常严重，同时这也提升我们需要让VAR模型有一定的自我纠错能力。

  沿着这个思路，Infinity在训练时提出了一种增强策略。在训练时的encoding阶段，量化token每位都会以$\sim\mathcal U(0,p)$的概率翻转，比如从1变成-1，将token map${\boldsymbol{R}_{k}}$变成了${\boldsymbol{R}_{k}^{f l i p}}$，后者是包含一定的错误。然后我们重新计算前${k}$个量化特征之和得到 $\boldsymbol{F}^{flip}_{k}$，而后计算这个包含错误的特征与输入的feature$\boldsymbol F$的残差${\boldsymbol F}-\boldsymbol F_k^{flip}$用来作为下一个scale的输入feature。整体算法如下：

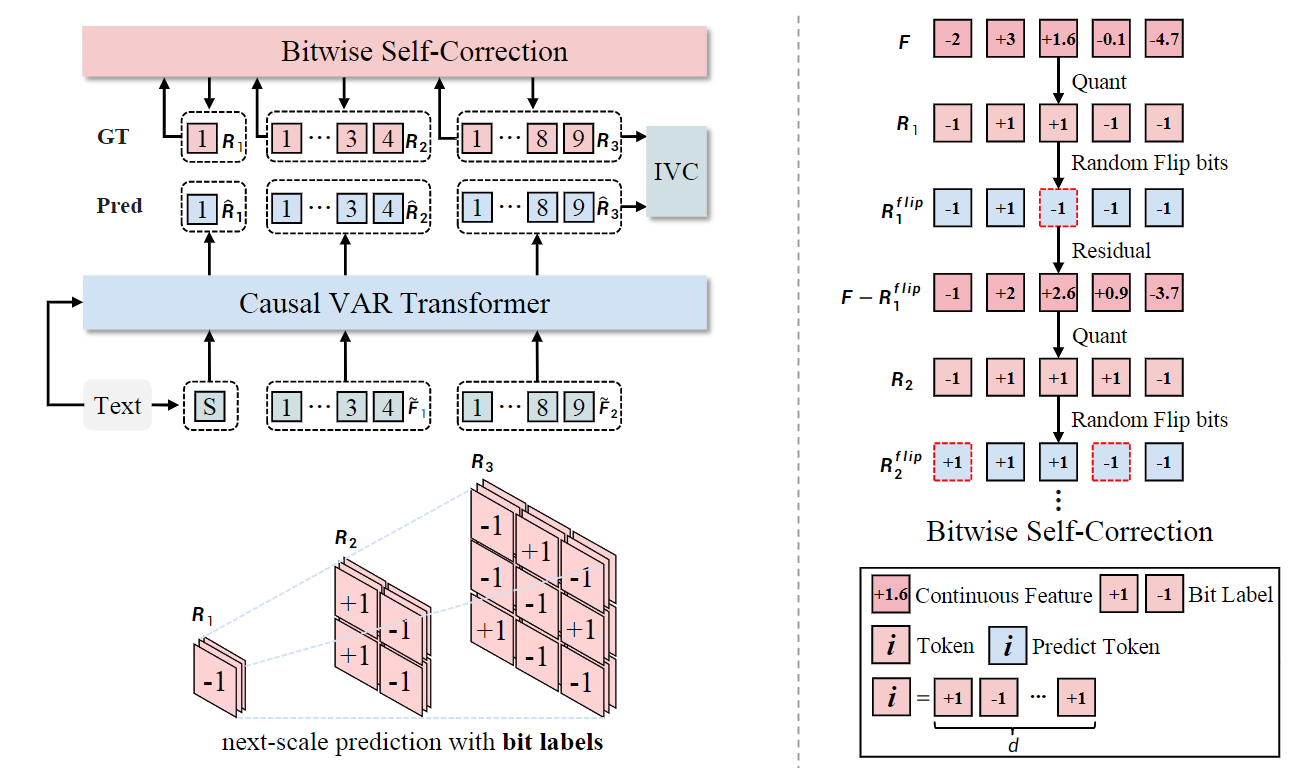
  简单来说BSC就是通过修改Transformer的输入和标签来实现，设在第$k$个scale时会翻转，在以$\boldsymbol{R}_{<k}$生成$\widetilde{\boldsymbol R}_k$时还是按未翻转作为GT；而将翻转后的作为下一次输入从而生成$\widetilde{\boldsymbol R}_{k+1}$，而此时的GT也对应修改。所以BSC相当于让模型学习不同的残差组合方式，从而增强对推理时scale的误差累计的鲁棒性。

这里右图的transformer输入有误，应该是[S]、第一个scale、第二个scale……这里[S]之后就直接是第二个scale的token map了。

其他细节

  除了BSQ、IVC和BSC这三个最主要的改进点之外，还有一些细节值得关注。文本特征使用Flan-T5提取，不仅映射为第一个embedding$\in\mathbb R^{B\times 1\times h}$生成第一个scale的token map；而且用cross attention加入（不知道为什么不用AdaLN）。此外Infinity和VAR最大的区别是支持不同分辨率的生成，这需要对不同的分辨率预先定义scale序列$\{(h_k,w_k)\}^K$。同时由于scale的不同，量化得到的token map数量也不同，因此VAR那种可学习的绝对位置编码就不适用了。Infinity使用了2D-RoPE，同时保留了可学习的scale embedding。训练的时候使用256->512->1024多阶段，这也是常规策略了。

总结

  具体的实验部分就不介绍了，我们在最开始已经看过了。总的来说Infinity最大的创新个人认为在于BSC。仔细看下来bitwise self-correction虽然也可以理解为在训练过程中“加噪”，但和diffusion的加噪还是很不同的。BSC本质上相当于模拟了推理时的误差累计，让模型学习在某个scale上出错的情况下能“圆回来”。

  不过不得不说故事讲的很好，起了Infinity名字，强行把codebook size变成$2^{64}$，超过了int32表示范围，圆了codebook无限大的故事。虽然也有一些实验证明了这种极端扩展的效果，不过文中没有给利用率的指标（当然这种情况下codebook利用率的计算也比较耗时），是否值得还是需要商榷的。

References

1. Infinity∞: Scaling Bitwise AutoRegressive Modeling for High-Resolution Image Synthesis, arXiv 2024 - Infinity
   Jian Han, Jinlai Liu, Yi Jiang, Bin Yan, Yuqi Zhang, Zehuan Yuan, Bingyue Peng, Xiaobing Liu @ByteDance, 2024.12| [[arXiv PDF]](https://arxiv.org/pdf/2412.04431)