前言
本文介绍DDPM算法,文章为[1]。
从DPM到DDPM
我们在上一篇文章中介绍了DPM的框架:
接下来我们就看看DDPM完善了哪些细节。
前向Markov核$q(\boldsymbol x_{t}|\boldsymbol x_{t-1})$
首先我们设前向Markov核$q(\boldsymbol x_{t}|\boldsymbol x_{t-1})\sim \mathcal N(\boldsymbol \mu_t,\boldsymbol \Sigma_t)$。下面我们详细讨论一下均值与协方差的具体形式。由我们的假设可知,任意时刻的噪音图像(专业术语为 latent)$\boldsymbol x^{(t)}$应该仅与上一时刻的latent:$\boldsymbol x_{t-1}$及一标准高斯噪声$\boldsymbol\varepsilon_t\sim \mathcal N(\boldsymbol 0, \boldsymbol I)$有关。由重参数技巧,我们设:
$$ \boldsymbol x_t=A_t\boldsymbol x_{t-1}+B_t \boldsymbol\varepsilon_t,\quad \boldsymbol\varepsilon_t\sim \mathcal N(\boldsymbol 0,\boldsymbol I)\tag{1} $$
因此:
$$ \begin{equation}\begin{aligned} \boldsymbol{x}_t =&\, A_t \boldsymbol{x}_{t-1} + B_t \boldsymbol{\varepsilon}_t \\ =&\, A_t \big(A_{t-1} \boldsymbol{x}_{t-2} + B_{t-1} \boldsymbol{\varepsilon}_{t-1}\big) + B_t \boldsymbol{\varepsilon}_t \\ =&\,\cdots\\ =&\,(A_t\cdots A_1) \boldsymbol{x}_0 + \underbrace{(A_t\cdots A_2)B_1 \boldsymbol{\varepsilon}_1 + (A_t\cdots A_3)B_2 \boldsymbol{\varepsilon}_2 + \cdots + A_tB_{t-1} \boldsymbol{\varepsilon}_{t-1} + B_t \boldsymbol{\varepsilon}_t}_{\boldsymbol\epsilon} \end{aligned}\label{eq:expand}\end{equation} $$
由于$\boldsymbol \varepsilon_i$独立同分布,因此$\boldsymbol\epsilon \sim \mathcal N\Big(\boldsymbol 0,(A_t\cdots A_2)^2B_1^2 + (A_t\cdots A_3)^2B_2^2 + \cdots + A_t^2B_{t-1}^2 + B_t^2\Big)$。由于均值已经是零向量了,那么很自然地我们希望:$\boldsymbol 0,(A_t\cdots A_2)^2B_1^2 + (A_t\cdots A_3)^2B_2^2 + \cdots + A_t^2B_{t-1}^2 + B_t^2=1$。最为简洁的设置是:
$$ A_i^2+B_i^2=1,\quad i=1,\cdots,t $$
如果我们取:$B_t=\sqrt{\beta_t}$,则立刻有$A_t=\sqrt{1-\beta_t}$。也即前向扩散核$q(\boldsymbol x_{t}|\boldsymbol x_{t-1})\sim \mathcal N(\sqrt{1-\beta_t} \boldsymbol x_{t-1},\beta_t\boldsymbol I)$。此时:
$$ \boldsymbol x_t=\sqrt{\bar{\alpha}_t}\boldsymbol x_0+\sqrt{1-\bar{\alpha}_t}\boldsymbol\epsilon,\quad,\bar{\alpha}_t=\prod_{k=0}^t (1-\beta_k),\; \boldsymbol\epsilon\sim \mathcal N(\boldsymbol 0,\boldsymbol I)\tag{2} $$
这样便极大地简化了正向扩散的过程,可以一步直接求出$\boldsymbol x_t$。如果我们对$\beta_t$设计一个scheduler使得$\bar{\alpha}_t\to 0$,便可以认为前向过程将$\boldsymbol x_0$(近似)完全转化为了标准高斯噪声。
训练目标
在DPM中我们的训练目标包括两部分:
$$ \begin{align} \min\mathcal L&=\min\Big(L_0+\sum_{t=2}^T L_t\Big)\\ where:\qquad L_0&=-\mathbb E_{q(\boldsymbol x_1|\boldsymbol x_0)}[\log p_{\boldsymbol\theta}(\boldsymbol x_0|\boldsymbol x_1)]\\ L_t&=\mathbb E_{q(\boldsymbol x_{t-1},\boldsymbol x_{t+1}|\boldsymbol x_0)}[KL(q(\boldsymbol x_t|\boldsymbol x_{t-1})\|p_{\boldsymbol\theta}(\boldsymbol x_t|\boldsymbol x_{t+1}))] \end{align}\tag{3} $$
对于$L_t$我们当然是用Monte Carlo进行估计,但我们需要对$\boldsymbol x_{t-1}$与$\boldsymbol x_{t+1}$进行估计,这在实践中可能导致方差过大的风险(采样的随机变量越多,越难以估计损失函数)。而且这个$\boldsymbol x_{t-1}$与$\boldsymbol x_{t+1}$还分别处于前向与反向两个不同的阶段,无端增加了计算量。因此我们希望将$L_t$中的$q(\boldsymbol x_t|\boldsymbol x_{t-1})$换成与$\boldsymbol x_{t+1}$有关的量。由Markov性:$q(\boldsymbol x_t|\boldsymbol x_{t-1})=q(\boldsymbol x_t|\boldsymbol x_{t-1},{\color{Red}\boldsymbol x_0})$,而且由Bayes定理:
$$ q(\boldsymbol x_t|\boldsymbol x_{t-1},\boldsymbol x_0)=\frac{q(\boldsymbol x_{t-1}|\boldsymbol x_t,\boldsymbol x_0)q(\boldsymbol x_t|\boldsymbol x_0)}{q(\boldsymbol x_{t-1}|\boldsymbol x_0)}\tag{4} $$
因此我们重新展开对数似然:(见[2])
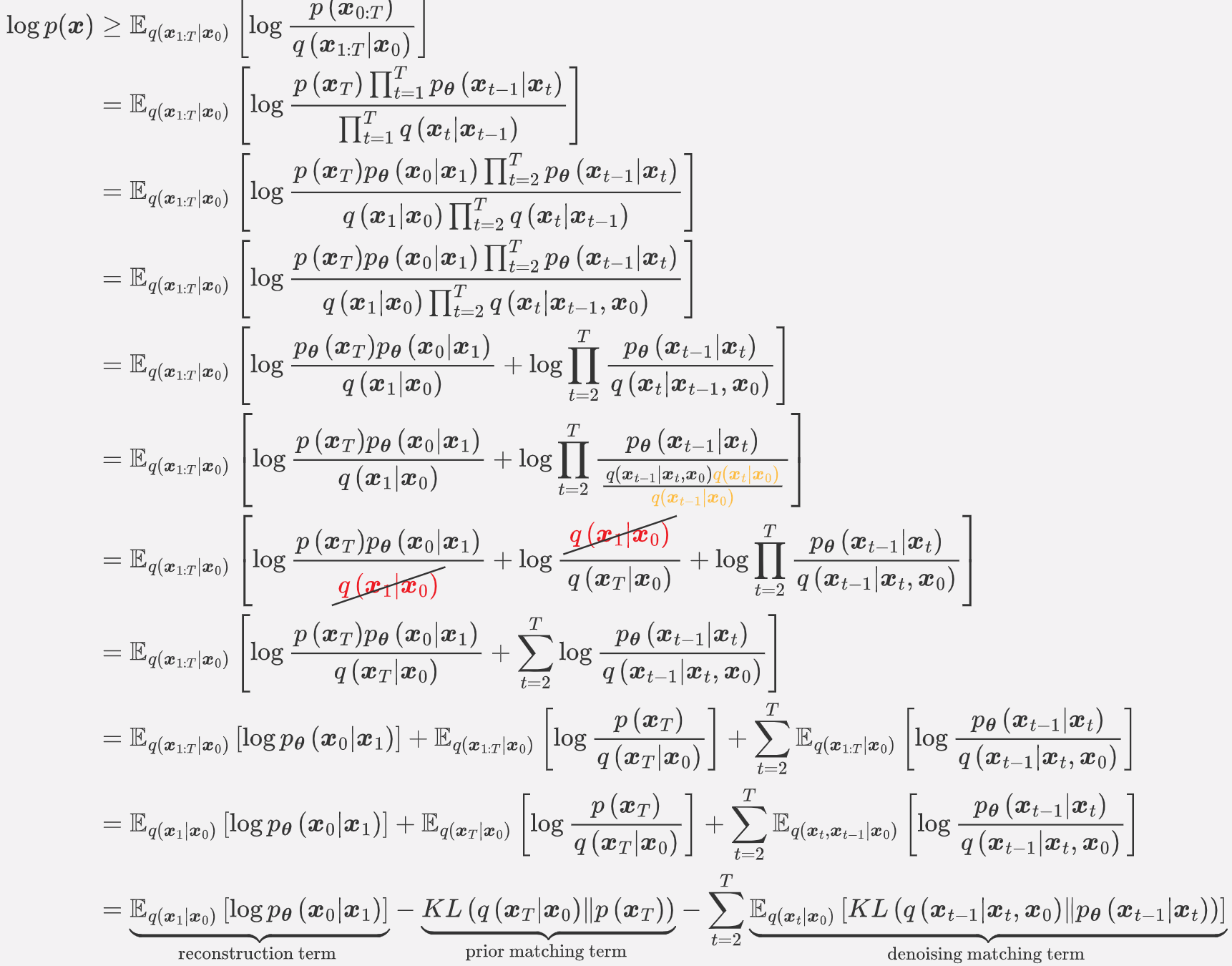
此时我们对比DPM中的推导,可见重建损失与先验匹配没有什么区别,唯一的区别是一致性指标:
$$ \mathbb E_{q(\boldsymbol x_{t-1},\boldsymbol x_{t+1}|\boldsymbol x_0)}[KL(q(\boldsymbol x_t|\boldsymbol x_{t-1})\|p_{\boldsymbol\theta}(\boldsymbol x_t|\boldsymbol x_{t+1}))] $$
变成了降噪匹配项:
$$ \mathbb{E}_{q\left(\boldsymbol{x}_{t} | \boldsymbol{x}_{0}\right)}\left[KL\left(q\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_{0}\right) \| p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}\right)\right)\right]\tag{6} $$
这样便将前向与后向之间的KL转换成了 真实降噪过程$q(\boldsymbol x_{t-1}|\boldsymbol x_t,\boldsymbol x_0)$与人为构造的参数化的降噪过程$p_{\boldsymbol\theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)$之间的KL,从而避免了方差过大的问题。
真实降噪过程$q(\boldsymbol x_{t-1}|\boldsymbol x_t,\boldsymbol x_0)$
那么现在又一个问题出现了,如何由:
$$ \begin{align} q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_{t}, \boldsymbol{x}_0) = q(\boldsymbol{x}_{t} | \boldsymbol{x}_{t - 1}, \boldsymbol{x}_0)\frac{q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_0)}{q(\boldsymbol{x}_{t} | \boldsymbol{x}_0)} \\ q(\boldsymbol{x}_{t} | \boldsymbol{x}_0)\sim\mathcal{N}(\boldsymbol{x}_{t}; \sqrt{\bar{\alpha}_t}\boldsymbol{x}_{0}, (1-\bar{\alpha}_t)\boldsymbol I)\\ q(\boldsymbol{x}_{t} | \boldsymbol{x}_{t-1}, \boldsymbol{x}_0)\sim\mathcal{N}(\boldsymbol{x}_{t};\sqrt{1 - \beta_t}\boldsymbol{x}_{t - 1},\beta_t\boldsymbol I) \end{align}\tag{7} $$
推导出$q(\boldsymbol x_{t-1}|\boldsymbol x_{t},\boldsymbol x_0)$的形式?(下面的推导以一维为例,$n$维同理类似)代入式子我们有:
$$ \begin{align} q( x_{t-1}|x_t, x_0)&=\frac{1}{\sqrt{2\pi\beta_t}}\exp\left(-\frac{(x_t-\sqrt{1-\beta_t}x_{t-1})^2}{2\beta_t} \right)\\ &\times \frac{1}{\sqrt{2\pi (1-\bar{\alpha}_{t-1})}}\exp\left(-\frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2}{2(1-\bar{\alpha}_{t-1})} \right)\\ &\times \sqrt{2\pi(1-\bar\alpha_{t})}\exp\left(\frac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{2(1-\bar\alpha_t)} \right)\\ &=\frac{1}{C(x_t,x_0)}\cdot\frac{1}{\sqrt{2\pi \cdot\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t}}\exp\left\{-\frac{1}{2}\left[\frac{\left[{\color{Red}x_{t-1}}- \left(\frac{\sqrt{1-\beta_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0 \right)\right]^2}{\left(\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \right)^2}\right] \right\} \end{align}\tag{8} $$
所以我们可以近似地认为:
$$ \begin{align} q(\boldsymbol x_{t-1}|\boldsymbol x_{t},\boldsymbol x_0)&\sim \mathcal N(\boldsymbol x_{t-1}; \tilde{\boldsymbol\mu}(\boldsymbol x_t,\boldsymbol x_0),\tilde{\boldsymbol\beta}_t)\\ where:\qquad \tilde{\boldsymbol\mu}(\boldsymbol x_t,\boldsymbol x_0)&=\frac{\sqrt{1-\beta_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}\boldsymbol x_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}\boldsymbol x_0\\ \tilde{\boldsymbol\beta}_t&=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t\cdot\boldsymbol I \end{align}\tag{9} $$
再由(2)式逆推消掉上式$\tilde{\boldsymbol \mu}(\boldsymbol x_t,\boldsymbol x_0)$中的$\boldsymbol x_0$:
$$ \tilde{\boldsymbol \mu}_t(\boldsymbol x_t)=\frac{1}{\sqrt{1-\beta_t}}\left(\boldsymbol x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\boldsymbol\epsilon \right)\tag{10} $$
这样我们便得到了(6)式中真实降噪过程$q(\boldsymbol x_{t-1}|\boldsymbol x_t,\boldsymbol x_0)$的具体形式。
最后:参数化降噪过程$p_{\boldsymbol\theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)$
现在,我们只需要确定我们构造的参数化降噪过程$p_{\boldsymbol\theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)$了。对于$q(\boldsymbol x_{t-1}|\boldsymbol x_t,\boldsymbol x_0)$,我们忽略了很多常数项才保住Gaussian的形式,那么自然而然地,我们取$p_{\boldsymbol\theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)$也为一高斯Markov核:
$$ p_{\boldsymbol\theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)\sim\mathcal N(\boldsymbol x_{t-1};\tilde{\boldsymbol \mu}_{\boldsymbol\theta}(\boldsymbol x_t),\tilde{\boldsymbol\beta}_{\boldsymbol\theta,t})\tag{11} $$
同时又注意到$\tilde{\boldsymbol \beta}_t$为一常数,没有学习的价值,因此我们取:$\tilde{\boldsymbol \beta}_{\boldsymbol\theta,t}=\tilde{\boldsymbol\beta}_t$,所以我们只需要让$\tilde{\boldsymbol \mu}_t(\boldsymbol x_t)$与$\tilde{\boldsymbol \mu}_{\boldsymbol\theta}(\boldsymbol x_t)$尽量接近即可。进一步地,观察(10)我们能发现,$\boldsymbol x_t$在去噪过程中是已知的,所以唯一具有不确定性的即是$\boldsymbol \epsilon_t$,所以我们只需要预测一个噪声$\boldsymbol\epsilon_{\boldsymbol\theta}(\boldsymbol x_t)$,使得其与生成$\boldsymbol x_t$的噪声$\boldsymbol\epsilon$的MSE最小即可。
最后的最后:训练与采样
当然上述表述略带直观,我们需要从(6)式出发得出最终的损失函数:
$$ L_t=\mathbb{E}_{\boldsymbol x_0,\boldsymbol\epsilon}\left[\frac{\beta_t^2}{2(1-\beta_t)(1-\bar{\alpha}_t)|\tilde{\boldsymbol \beta}_t|^2}\|\boldsymbol\epsilon-\boldsymbol\epsilon_{\boldsymbol\theta}(\boldsymbol x_t) \|^2 \right]\tag{12} $$
忽略掉常数项与重建损失$L_0$,则训练损失函数为:
$$ L_{simple}=\mathbb{E}_{\boldsymbol x_0,\boldsymbol\epsilon}\bigg[\|\boldsymbol\epsilon-\boldsymbol\epsilon_{\boldsymbol\theta}(\boldsymbol x_t) \|^2 \bigg]\tag{13} $$
(从结果来看看,确实很 simple!)
但如果直接将整个重建过程的$L_{simple}$之和作为损失函数,即:$\sum_{t=1}^T L_{simple, t}$,由于$T$往往特别大,训练效率将极其低下。因此,DDPM的作者创造性地随机在重建过程中取一个$L_{simple,t}$作为最终的训练损失,也即:
$$ L=\mathbb{E}_{t\sim\mathcal U\{1,\cdots,t\},\boldsymbol x_0\sim q(\boldsymbol x_0),\boldsymbol\epsilon\sim \mathcal N(\boldsymbol 0,\boldsymbol I)}\bigg[\|\boldsymbol\epsilon-\boldsymbol\epsilon_{\boldsymbol\theta}(\boldsymbol x_t) \|^2 \bigg]\tag{14} $$
训练好之后,我们就可以从$\boldsymbol x_t$执行$T$次(11)式得到最终的结果了。同时为了加入随机性,每一步加上$\tilde{\boldsymbol\beta}_t\boldsymbol z,\boldsymbol z\sim\mathcal N(\boldsymbol 0,\boldsymbol I)$。
训练与采样的流程如下:
![训练与采样(图源[1])](https://hjhgjghhg-1304275113.cos.ap-shanghai.myqcloud.com/usr/img/Diffusion%20Model%EF%BC%88%E4%BA%8C%EF%BC%89%EF%BC%9ADDPM/%E8%AE%AD%E7%BB%83%E4%B8%8E%E9%87%87%E6%A0%B7.png)
References
- Denoising Diffusion Probabilistic Models, NeurIPS 2020 -DDPM
Jonathan Ho, Ajay Jain, Pieter Abbeel [[NeurIPS pdf]](https://proceedings.neurips.cc//paper/2020/file/4c5bcfec8584af0d967f1ab10179ca4b-Paper.pdf) [[arXiv pdf]](https://arxiv.org/pdf/2006.11239.pdf) - Understanding Diffusion Models: A Unified Perspective, arXiv
Calvin Luo, 2022 [[arXiv pdf]](https://arxiv.org/pdf/2208.11970.pdf) - 生成扩散模型漫谈(一):DDPM = 拆楼 + 建楼
- How diffusion models work: the math from scratch
- Course:CPSC522/Diffusion Probabilistic Model
- What are Diffusion Models?
