Diffusion Model（一）：概述与框架

前言

  本文我们介绍扩散模型的框架。如果读者对随机分析有了解的话，提起“扩散”应该会立刻联想起Ito过程或者SDE；而其他（特别是有物理背景）的读者或许会想到热力学的相关东西。事实上扩散模型也确实可以从多个视角理解，作为本系列的第一篇，本文介绍扩散模型思想的开山之作：Deep Unsupervised Learning using Nonequilibrium Thermodynamics, ICML 2015 [1]。由于这篇文章是从概率视角提出了一种模型框架，因此有的文章也把这个框架称为Diffusion Probabilistic Model (DPM)。

思路

  大家或多或少应该了解过扩散模型的大致思路：首先通过一个Markov过程向真实数据分布中添加噪声，经过$T$步得到一个simple, tractable的分布（例如$\mathcal N(\boldsymbol 0,\boldsymbol I)$），如果模型能学会该过程，那么反过来，模型就能实现从随机噪音得到真实数据。接下来我们详细讨论“前向”和“后向”两个阶段。

前向

  设真实数据服从分布：$\boldsymbol x_0\sim q(\boldsymbol x_0)$（事实上$\boldsymbol x_0$是某个服从$q(\boldsymbol x_0)$的随机变量$X_0$采样得到的样本，由于额外研究$X_0$没有过多意义，在下文中我们不额外区分$X_0$和$\boldsymbol x_0$，下文也并非严谨的数学语言，理解意思即可）。我们通过一个Markov扩散核函数$T_{\pi}(\boldsymbol y|\boldsymbol y';\beta)$将其转变为另一分布$\pi(\boldsymbol y)$。其中$\beta$为扩散系数。显然地：

$$ \pi(\boldsymbol y) = \int T_\pi(\boldsymbol y|\boldsymbol y;\beta)\pi(\boldsymbol y')\text d\boldsymbol y'\tag{1} $$

  记：

$$ q(\boldsymbol x_{t}|\boldsymbol x_{t-1})=T_\pi(\boldsymbol x_{t}|\boldsymbol x_{t-1};\beta_t)\tag{2} $$

  由Markov性，我们有：

$$ q(\boldsymbol x_{0\cdots T})=q(\boldsymbol x_0)q(\boldsymbol x_1|\boldsymbol x_0)q(\boldsymbol x_2|\boldsymbol x_1,\boldsymbol x_0)\cdots q(\boldsymbol x_T|\boldsymbol x_{T-1},\cdots ,\boldsymbol x_0)=q(\boldsymbol x_0)\prod_{t=1}^T q(\boldsymbol x_T|\boldsymbol x_{T-1})\tag{3} $$

其中$q(\boldsymbol x_{0\cdots T})=q(\boldsymbol x_{0},\cdots,\boldsymbol x_{T}$。为了方便计算，我们不妨取kernel为：

$$ q(\boldsymbol x_{t}|\boldsymbol x_{t-1})=T_\pi(\boldsymbol x_{t}|\boldsymbol x_{t-1};\beta_t)\sim \mathcal N(\boldsymbol \mu_t,\boldsymbol \Sigma_t) \tag{4} $$

  此处从$\boldsymbol x_{t-1}$到$\boldsymbol x_t$的Markov核$q(\boldsymbol x_t|\boldsymbol x_{t-1})$的意思即是：

$$ \boldsymbol x_t\sim q(\boldsymbol x_{t}|\boldsymbol x_{t-1}) $$

这里$q$表示分布，不要被写法误导认为$q(\boldsymbol x|\boldsymbol x_{t-1})$是条件概率了~

![Latent samples（图源[1]）](https://hjhgjghhg-1304275113.cos.ap-shanghai.myqcloud.com/usr/img/Diffusion%20Model%EF%BC%88%E4%B8%80%EF%BC%89%EF%BC%9A%E6%A6%82%E8%BF%B0%E4%B8%8E%E6%A1%86%E6%9E%B6/Latent%20samples.png)

其中均值与协方差的具体形式我们还不知道，唯一知道的是$\boldsymbol \mu_t$与$\boldsymbol\Sigma_t$仅与上一时刻的latent：$\boldsymbol x_{t-1}$及一标准高斯噪声$\boldsymbol\varepsilon_t\sim \mathcal N(\boldsymbol 0, \boldsymbol I)$有关。
  这样我们便完成了从真实分布$q(\boldsymbol x_0)$到高斯噪音的“拆解”。

反向

  现在我们只需要完成完全相反的逆过程就可实现从$\boldsymbol z\sim \mathcal N(\boldsymbol 0, \boldsymbol I)$到真实数据分布的转换。可问题是反向过程是从$T$到$0$，$\boldsymbol x_{t-1}$对$\boldsymbol x_t$是不可见的，仅在少数情况下能解析地求解$\boldsymbol x_{t-1}$。此处我们不妨假设我们同样使用$T$步的参数化的Markov核$p_{\boldsymbol \theta}(\boldsymbol x_{t-1}|\boldsymbol x_t),t=T,\cdots,1$将$\boldsymbol x_T$转换成$\boldsymbol x_0$，其中$p_{\boldsymbol \theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)$对标的是$q(\boldsymbol x_t|\boldsymbol x_{t-1})$。类似（3）式，我们有：

$$ p_{\boldsymbol \theta}(\boldsymbol x_{0,\cdots,T})=p_{\boldsymbol \theta}(\boldsymbol x_T)\prod_{t=1}^Tp_{\boldsymbol \theta}(\boldsymbol x_{t-1}|\boldsymbol x_{t})\tag{7} $$

似然

  显然地下一步我们便是极大化对数似然：

$$ \max \log p_{\boldsymbol \theta}(\boldsymbol x_0)\tag{8} $$

对$\log p_{\boldsymbol \theta}(\boldsymbol x_0)$展开可得：（以下来源于[2]）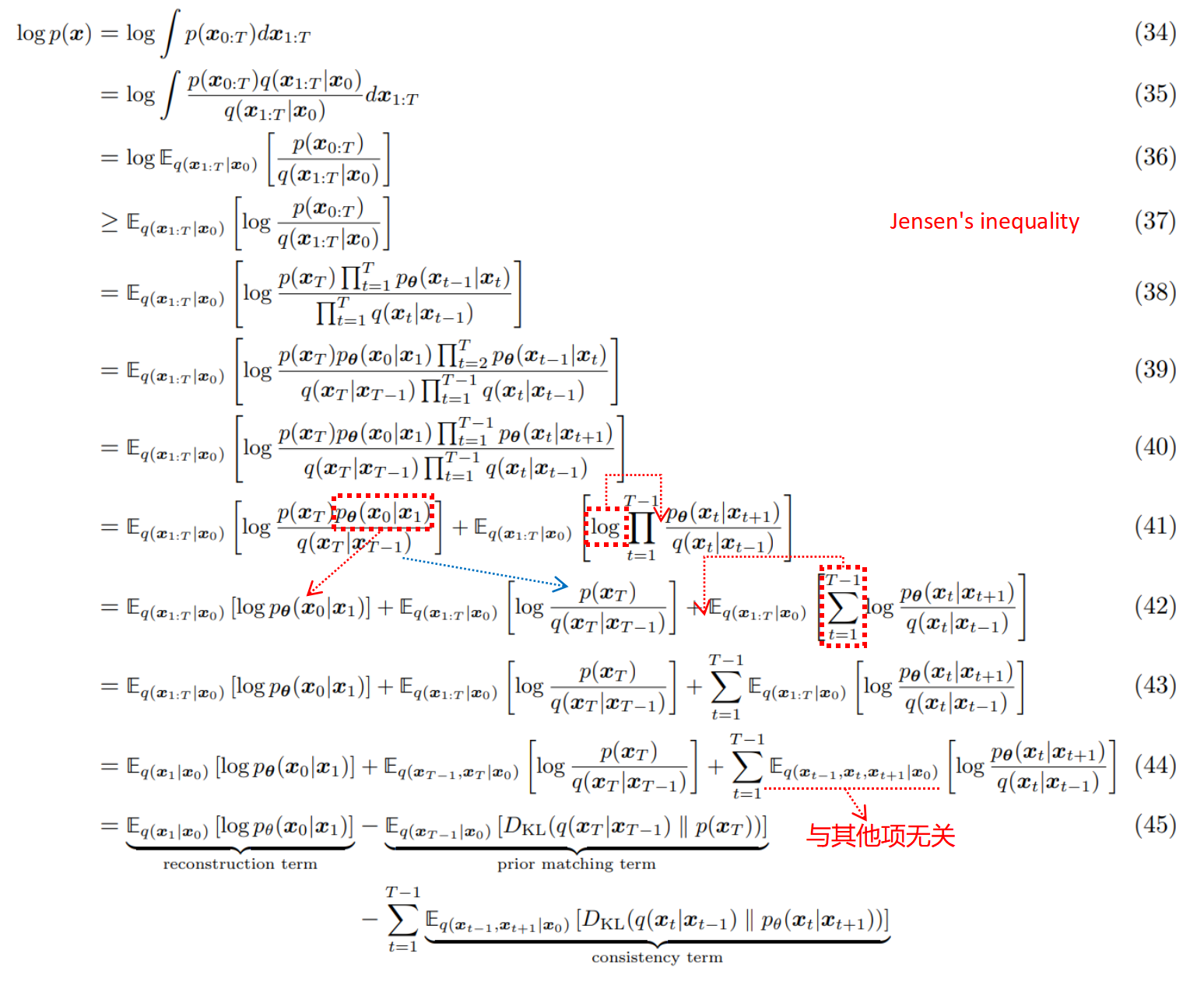

  其分成了三个部分，我们拆解分析一下：

（1）$L_0=-\mathbb E_{q(\boldsymbol x_1|\boldsymbol x_0)}[\log p_{\boldsymbol\theta}(\boldsymbol x_0|\boldsymbol x_1)]$，重建概率：刻画的是给定第一步latent：$\boldsymbol x_1$（从反向的过程来看是最后一步latent）重建得到$\boldsymbol x_0$的对数概率期望；

（2）$L_T=KL(q(\boldsymbol x_{T-1}|\boldsymbol x_0)\| p(\boldsymbol x_T))$，先验匹配：刻画前向的最后一步latent$\boldsymbol x_{t-1}$与标准高斯噪声的差异。这一项中没有可训练的参数，可以忽略。而且直观上而言当$T\to \infty$，应该有$L_T\to 0$。

（3）$L_t=\mathbb E_{q(\boldsymbol x_{t-1},\boldsymbol x_{t+1}|\boldsymbol x_0)}[KL(q(\boldsymbol x_t|\boldsymbol x_{t-1})|p_{\boldsymbol\theta}(\boldsymbol x_t|\boldsymbol x_{t+1}))]$，一致性指标：刻画的是从$\boldsymbol x_{t-1}$前向得到的$\boldsymbol x_t$与从$\boldsymbol x_{t-1}$反向重建得到的$\boldsymbol x_t$之间的差异（用KL散度刻画）。

总结

![DPM流程（图源[2]）](https://hjhgjghhg-1304275113.cos.ap-shanghai.myqcloud.com/usr/img/Diffusion%20Model%EF%BC%88%E4%B8%80%EF%BC%89%EF%BC%9A%E6%A6%82%E8%BF%B0%E4%B8%8E%E6%A1%86%E6%9E%B6/DPM%E6%B5%81%E7%A8%8B.png)

  我们总结一下DPM提出了一个怎样的框架。首先从真实数据分布$\boldsymbol x_0$开始，通过一系列的Markov核$q(\boldsymbol x_t|\boldsymbol x_{t-1})$变换为（近似）标准高斯噪声$\boldsymbol x_T$；而后再通过一参数化的Markov核$p_{\boldsymbol \theta}(\boldsymbol x_{t-1}|\boldsymbol x_t)$将标准高斯噪声重建为真实数据分布。整体架构的训练任务为：

$$ \begin{align} \min\mathcal L&=\min\Big(L_0+\sum_{t=2}^T L_t\Big)\\ where:\qquad L_0&=-\mathbb E_{q(\boldsymbol x_1|\boldsymbol x_0)}[\log p_{\boldsymbol\theta}(\boldsymbol x_0|\boldsymbol x_1)]\\ L_t&=\mathbb E_{q(\boldsymbol x_{t-1},\boldsymbol x_{t+1}|\boldsymbol x_0)}[KL(q(\boldsymbol x_t|\boldsymbol x_{t-1})|p_{\boldsymbol\theta}(\boldsymbol x_t|\boldsymbol x_{t+1}))] \end{align} $$

  可显然地，DPM仅仅只是一个框架，离实际使用还有很多问题需要回答。例如前向过程的$\boldsymbol \mu_t$与$\boldsymbol \Sigma_t$如何确定？后向的参数化核$p_{\boldsymbol\theta}(\cdot,\cdot)$如何设计？真正完善DPM使其大放异彩，则要等到5年之后的《Denoising Diffusion Probabilistic Model》了。

References

1. Deep Unsupervised Learning using Nonequilibrium Thermodynamics, ICML 2015
   Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, Surya Ganguli, 2015.03 [[ICML pdf]](http://proceedings.mlr.press/v37/sohl-dickstein15.pdf) [[arXiv pdf]](https://arxiv.org/pdf/1503.03585.pdf) [[Project]](https://github.com/Sohl-Dickstein/Diffusion-Probabilistic-Models)
2. Understanding Diffusion Models: A Unified Perspective, arXiv
   Calvin Luo, 2022 [[arXiv pdf]](https://arxiv.org/pdf/2208.11970.pdf)