前言
本章我们介绍VAE的结构与思路。
自编码器(AE)
自编码器(Auto-Encoder,AE)是 无监督表征学习 的经典算法,其包含一个编码器(Encoder):$f:=\mathbb{R}^n\to\mathbb{R}^d$;与一个解码器(Decoder):$g:=\mathbb{R}^d\to\mathbb{R}^n$。AE的底层逻辑仍然是神经网络的通用近似定理,因此其天然适合压缩、重建等学习恒等映射的任务。
但此时每个数据被映射至一个固定向量,从 生成任务 的视角看该表征学习方法发生了严重的过拟合。一个简单的解决办法是 将输入映射到分布! 李宏毅老师的这张图[1]很能说明问题:
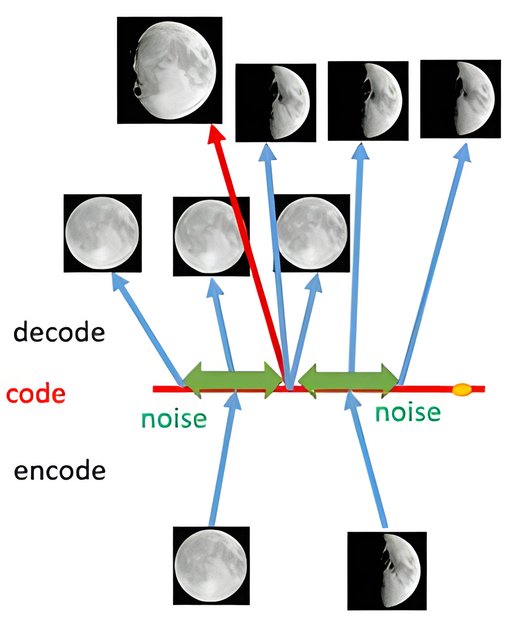
那么,现在出现了两个最大的问题: 加入什么噪音呢?如何加入噪音呢? 变分自编码器(VAE)给出了这两个问题的答案。
变分自编码器(VAE)
Kingma(Adam的作者之一)与Welling首次对这两个问题进行了完成的推导与阐述 [3]。我们首先回顾生成问题:设有一批独立同分布的数据样本$\{\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}\}$,我们希望通过某种参数化方法得到其分布$p_{\boldsymbol{\theta}}(\boldsymbol{x})$,迂回一下则有:
$$ p_{\boldsymbol\theta}\left(\boldsymbol{x}\right)=\int p_{\boldsymbol\theta}\left(\boldsymbol{x} | \boldsymbol{z}\right) p_{\boldsymbol\theta}(\boldsymbol{z}) d \boldsymbol{z} \tag{1} $$
我们首先明确几个概念:
- 先验:$p_{\boldsymbol\theta}(\boldsymbol{z})$
- 条件:$p_{\boldsymbol\theta}\left(\boldsymbol{x} | \boldsymbol{z}\right)$
- 后验:$p_{\boldsymbol\theta}\left(\boldsymbol{z} | \boldsymbol{x}\right)$
对于第一个问题,由:Wiener's Tauberian theorem [2],先验可简单取为标准高斯分布:$\boldsymbol{z}\sim \mathcal{N}(\boldsymbol 0,\boldsymbol{\mathrm I})$。在此观点下,VAE可视为由若干个高斯分布的混合,每个输入对应一个高斯分布。也即我们的目标是先将输入映射至(接近)高斯分布,再从其中还原。
作者或许受到了EM算法的影响,针对EM算法无法应用于本问题的缺陷,考虑了难以直接计算的后验:$p_{\boldsymbol\theta}\left(\boldsymbol{z} | \boldsymbol{x}\right)$。我们先按照原论文的思路理解一遍VAE。
推断
为了保持灵活性,我们将后验记为:$q_{\boldsymbol\phi}\left(\boldsymbol{z} | \boldsymbol{x}\right)$。为了简便我们取:$\boldsymbol\phi\sim \mathcal N(\boldsymbol 0, \boldsymbol{\mathrm I})$。为了体现上文介绍的专属性,使用神经网络为每个输入对应的后验配上$\boldsymbol \mu$和$\boldsymbol \sigma^2$,也即原论文中说的:
..., we’ll assume the true (but intractable) posterior takes on a approximate Gaussian form with an approximately diagonal covariance. In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:
$$ \log q_{\boldsymbol{\phi}}\left(\boldsymbol{z} | \boldsymbol{x}^{(i)}\right)=\log \mathcal{N}\left(\boldsymbol{z} ; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)} \boldsymbol{\mathrm I}\right) $$
where the mean and s.d. of the approximate posterior, $\boldsymbol \mu^{(i)}$ and $\boldsymbol\sigma^{(i)}$, are outputs of the encoding MLP, i.e. nonlinear functions of datapoint $\boldsymbol x^{(i)}$ and the variational parameters $\boldsymbol \phi$.
值得注意的是,为了满足$\boldsymbol{z}\sim \mathcal{N}(\boldsymbol 0,\boldsymbol{\mathrm I})$的假设,我们需要约束$q_{\boldsymbol\phi}(\boldsymbol z | \boldsymbol x^{(i)})$向标准正态分布对齐。这是由于:
$$ p_{\boldsymbol\theta}(\boldsymbol z)=\int p_{\boldsymbol\theta}(\boldsymbol z|\boldsymbol x)p_{\boldsymbol\theta}(\boldsymbol x)\text d\boldsymbol x=\mathcal N(\boldsymbol 0,\boldsymbol{\mathrm I}) \tag{2} $$
现在,我们完成了第一步“推断”,通过神经网络“求解”后验$q_{\boldsymbol\phi}\left(\boldsymbol{z} | \boldsymbol{x}\right)$,从而将输入$\{\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}\}$映射至服从标准正态分布的隐变量$\boldsymbol z$。
损失函数
接下来就是从后验$q_{\boldsymbol\phi}\left(\boldsymbol{z} | \boldsymbol{x}\right)$中重建分布了。回到最开始要求解的目标式:$p_{\boldsymbol\theta}\left(\boldsymbol{x}\right)=\int p_{\boldsymbol\theta}\left(\boldsymbol{x} | \boldsymbol{z}\right) p_{\boldsymbol\theta}(\boldsymbol{z}) d \boldsymbol{z}$,由极大似然,我们需要最大化:
$$ \max_{\boldsymbol \theta} L_{\boldsymbol\theta}=\max_{\boldsymbol\theta} \sum_{\boldsymbol x}\log p_{\boldsymbol\theta}(\boldsymbol x) \tag{3} $$
其中:
$$ \begin{align*} \log p_{\boldsymbol \theta}(\boldsymbol{x})&=\int q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x}) \log p_{\boldsymbol \theta}(\boldsymbol{x}) \text d \boldsymbol{z} \tag{4}\\ &=\int q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x}) \log \left(\frac{p_{\boldsymbol \theta}(\boldsymbol{z}, \boldsymbol{x})}{p_{\boldsymbol \theta}(\boldsymbol{z} | \boldsymbol{x})}\right) \text d \boldsymbol{z}=\int q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x}) \log \left(\frac{p_{\boldsymbol \theta}(\boldsymbol{z}, \boldsymbol{x})}{q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x})} \frac{q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x})}{p_{\boldsymbol \theta}(\boldsymbol{z} | \boldsymbol{x})}\right) \text d \boldsymbol{z} \tag{5}\\ &=\underbrace{\int q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x}) \log \left(\frac{p_{\boldsymbol \theta}(\boldsymbol{z}, \boldsymbol{x})}{q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x})}\right) \text d \boldsymbol{z}}_{ELBO}+\underbrace{\int q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x}) \log \left(\frac{q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x})}{p_{\boldsymbol \theta}(\boldsymbol{z} | \boldsymbol{x})}\right) \text d \boldsymbol{z}}_{KL}\tag{6} \\ &\underbrace{\geq \int q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x}) \log \left(\frac{p_{\boldsymbol \theta}(\boldsymbol{x} | \boldsymbol{z}) p_{\boldsymbol \theta}(\boldsymbol{z})}{q_{\boldsymbol \phi}(\boldsymbol{z} | \boldsymbol{x})}\right) \text d \boldsymbol{z} }_{ELBO} \tag{7} \end{align*} $$
(6)式中第二项为KL散度:$KL(q_{\boldsymbol\phi}(\boldsymbol z|\boldsymbol x)\|p_{\boldsymbol\theta}(\boldsymbol z|\boldsymbol x))$;第一项记为证据下界ELBO(Evidence Lower Bound)。由于KL散度$\geq 0$,所以:
$$ \begin{align} \max_{\boldsymbol\theta}\sum_{\boldsymbol x}\log p_{\boldsymbol\theta}(\boldsymbol x)&=\max_{\boldsymbol\theta}\sum_{\boldsymbol x}ELBO(\boldsymbol x;\boldsymbol\theta,\boldsymbol\phi)\\ &=\max_{\boldsymbol\theta} \mathbb{E}_{\boldsymbol z\sim q_{\boldsymbol\phi}(\boldsymbol z|\boldsymbol x)}\log p_{\boldsymbol\theta}(\boldsymbol x|\boldsymbol z) -KL(q_{\boldsymbol \phi}(\boldsymbol z|\boldsymbol x)\| p_{\boldsymbol \theta}(\boldsymbol z))\tag{8} \end{align} $$
对于$\log p_{\boldsymbol\theta}(\boldsymbol x| \boldsymbol z)$直接说结果:若$\boldsymbol x$为二值向量,需要对decoder用sigmoid函数激活,然后用交叉熵作为损失函数,这相当于$p_{\boldsymbol \theta}(\boldsymbol x| \boldsymbol z)$取伯努利分布;其余一般情况下我们用MSE作为损失函数,这相当于$p_{\boldsymbol \theta}(\boldsymbol x| \boldsymbol z)$取高斯分布。推导可参考[4]与论文的Appendix C。
对于$KL(q_{\boldsymbol \phi}(\boldsymbol z|\boldsymbol x)\| p_{\boldsymbol \theta}(\boldsymbol z))$,通常可直接计算。给定$D$维空间中的两个正态分布$\mathcal{N}\left(\boldsymbol\mu_{1}, \boldsymbol{\Sigma}_{1}\right)$和$\mathcal{N}\left(\boldsymbol\mu_{2}, \boldsymbol{\Sigma}_{2}\right)$, 其$\mathrm{KL}$散度为:
$$ \begin{align} &KL\left(\mathcal{N}\left(\boldsymbol\mu_{1},\boldsymbol{\Sigma}_{1}\right)\|\mathcal{N}\left(\boldsymbol\mu_{2}, \boldsymbol{\Sigma}_{2}\right)\right)\\ =\ &\frac{1}{2}\left(\operatorname{tr}\left(\boldsymbol{\Sigma}_{2}^{-1} \boldsymbol{\Sigma}_{1}\right)+\left(\boldsymbol\mu_{2}-\boldsymbol\mu_{1}\right)^{\top} \boldsymbol{\Sigma}_{2}^{-1}\left(\boldsymbol\mu_{2}-\boldsymbol\mu_{1}\right)-D+\log \frac{\left|\boldsymbol{\Sigma}_{2}\right|}{\left|\boldsymbol{\Sigma}_{1}\right|}\right) \end{align}\tag{9} $$
所以,代入:$p_{\boldsymbol\theta}(\boldsymbol z)=\mathcal N(\boldsymbol 0,\boldsymbol{\mathrm I}),\ q_{\boldsymbol \phi}(\boldsymbol z|\boldsymbol x)=\mathcal N(\boldsymbol\mu, \boldsymbol\sigma^2)$,则:
$$ \begin{align} KL(q_{\boldsymbol \phi}(\boldsymbol z|\boldsymbol x)\| p_{\boldsymbol \theta}(\boldsymbol z))&=\frac 12\Bigg(\text{tr}(\boldsymbol\sigma^2\boldsymbol{\mathrm I})+\boldsymbol\mu^\top\boldsymbol\mu-d-\log(|\boldsymbol\sigma^2\boldsymbol{\mathrm I}|) \Bigg)\\ &=\frac 12 \sum_{i=1}^d \Big(\sigma^{2(i)}+\mu^{2(i)}-\log \sigma^{2(i)}-1 \Big) \end{align} \tag{10} $$
总体而言,8式的第二项为后验与先验之间的距离,也即我们在推断部分约束$q_{\boldsymbol\phi}(\boldsymbol z | \boldsymbol x^{(i)})$向标准正态分布对齐的部分;而第一项则是常规重建损失。[5]中的一个公式更清晰地展示了损失的各个部分:
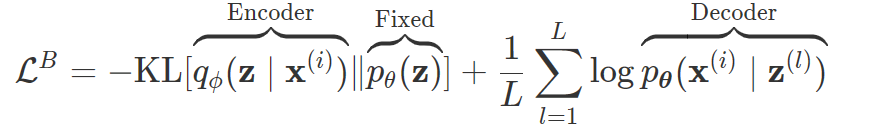
最后一公里
最后还有一个小细节,对于8式的第一项:$\mathbb{E}_{\boldsymbol z\sim q_{\boldsymbol\phi}(\boldsymbol z|\boldsymbol x)}\log p_{\boldsymbol\theta}(\boldsymbol x|\boldsymbol z)$,此时我们是按分布$q_{\boldsymbol\phi}(\boldsymbol z|\boldsymbol x)$来采样$\boldsymbol z$的。采样是一个随机过程,因此不能反向传播梯度。为了使其可训练,作者引入了重新参数化技巧(The Reparameterization Trick)。注意到:(以一元情况为例)
$$ \begin{aligned}&\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(z-\mu)^2}{2\sigma^2}\right)dz \\ =\ & \frac{1}{\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\frac{z-\mu}{\sigma}\right)^2\right]d\left(\frac{z-\mu}{\sigma}\right)\end{aligned}\tag{11} $$
从而我们有结论:
从$\mathcal{N}(\mu,\sigma^2)$中采样一个$z$,相当于从$\mathcal{N}(0,\mathrm I)$中采样一个$\varepsilon$,然后让$Z=\mu + \varepsilon \times \sigma$。
自此,VAE最核心的部分介绍完毕了,其网络结构如下图所示(图源[8]):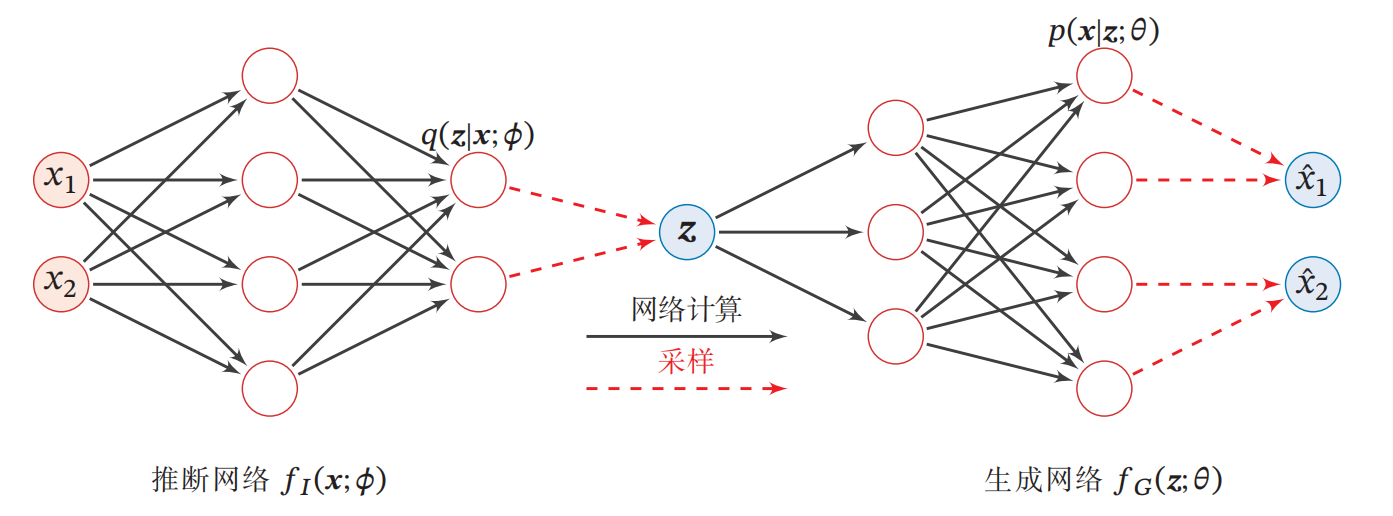
可见两个参数:$\boldsymbol\phi$和$\boldsymbol\theta$分别为推断网络(Encoder)和生成网络(Decoder)的参数。下一章我们将结合代码进一步深入理解VAE。
References
- https://www.bilibili.com/video/av15889450/?p=33
- Wiener's Tauberian theorem
- Diederik P Kingma, Max Welling, Auto-Encoding Variational Bayes [[v11 PDF]](https://arxiv.org/pdf/1312.6114.pdf)
- https://spaces.ac.cn/archives/5343/comment-page-7#%E7%94%9F%E6%88%90%E6%A8%A1%E5%9E%8B%E8%BF%91%E4%BC%BC
- 变分自编码器(一):原来是这么一回事
- The Reparameterization Trick (gregorygundersen.com)
- (四)2022-11-07 VAE & GAN - 知乎 (zhihu.com)
- 邱锡鹏,神经网络与深度学习
