优化器十六：AdamW

前言

  本文介绍AdamW算法。

$L_2$正则

  在机器学习建模过程中，正则化是控制模型复杂度，对抗过拟合，增强鲁棒性，追求更优预测效果的重要手段。而参数范数惩罚作为最古老而有效的正则化策略在深度学习出现之前就已经被使用了数十年。考虑ERM框架，设有数据集$\boldsymbol{T}$上的损失函数$L(\boldsymbol{\theta},\boldsymbol{T})$，则添加参数范数惩罚后的正则化损失为：

$$ L^{reg}(\boldsymbol{\theta},\boldsymbol{T})=L(\boldsymbol{\theta},\boldsymbol{T})+\alpha \Omega(\boldsymbol{\theta})\tag{1} $$

其中$\alpha\in[0,\infty)$为平衡范数惩罚项与标准目标函数的超参。在所有范数惩罚项中，$L_2$正则应用最为广泛。其形式为：

$$ L^{reg}(\boldsymbol{\theta},\boldsymbol{T})=L(\boldsymbol{\theta},\boldsymbol{T})+\frac{\alpha}{2}\|\boldsymbol{\theta}\|_2^2 \tag{2} $$

  关于如何理解$L_2$正则，有从Ridge回归角度分析的，有从贝叶斯推断角度分析的，还有从抗干扰性与鲁棒性角度理解的，更多内容可参见[1]，这里就不展开了。

权重衰减

  那么应用了$L_2$正则后的参数迭代具有怎样的形式呢？我们先来看SGD，设原来的迭代式为：$\boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta\cdot \boldsymbol{g}^{(\tau)}$，容易证明，添加了正则化项：$\frac{\lambda}{2\eta}\|\boldsymbol{\theta}^{(\tau)}\|_2^2$后，迭代式变为：

$$ \boldsymbol{\theta}^{(\tau+1)}=(1-\lambda)\boldsymbol{\theta}^{(\tau)}-\eta\cdot \boldsymbol{g}^{(\tau)}\tag{3} $$

由于$0<1-\lambda<1$，这会使得整个优化过程中参数$\boldsymbol{\theta}$有“收缩”到0的倾向，于是Hanson & Pratt称这种迭代方式为“权重衰减”（Weight Decay）。由于$L_2$正则与权重衰减的等价性，这两个概念一直混淆不清，甚至一度作为对方的别称。在实际实现中，以下两种方式都存在，且是等价的：

  而在自适应算法中这种等价性是否还存在呢？我们来研究研究。设有正则化的损失：$L^{reg}(\boldsymbol{\theta}^{(\tau)},\boldsymbol{T})=L(\boldsymbol{\theta}^{(\tau)},\boldsymbol{T})+\frac{\lambda'}{2}\|\boldsymbol{\theta}^{(\tau)}\|_2^2$，其梯度为：$\boldsymbol{g}^{(\tau)}_{reg}=\boldsymbol{g}^{(\tau)}+\lambda'\boldsymbol{\theta}^{(\tau)}$，某个自适应算法的迭代式为：

$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta\cdot\boldsymbol{M}^{(\tau)}\cdot \boldsymbol{g}^{(\tau)}_{reg}=\boldsymbol{\theta}^{(\tau)} -\eta\cdot \boldsymbol{M}^{(\tau)}\cdot \boldsymbol{g}^{(\tau)}-\eta\lambda'\cdot \boldsymbol{M}^{(\tau)}\cdot \boldsymbol{\theta}^{(\tau)}\tag{4} $$

其中$\boldsymbol{M}$为某个自适应算子，例如在AdaGrad中$\boldsymbol{M}^{(\tau)}=1/\sqrt{\varepsilon\boldsymbol{1}+\sum\limits_{k=1}^{\tau}\boldsymbol{g}^{(k)} \odot\boldsymbol{g}^{(k)} }$，由于是自适应算法而不是SGD，则必有：

$$ \boldsymbol{M}\neq k\boldsymbol{I}\tag{5} $$

  现在设式（4）与权重衰减项等价，即存在$\lambda$使得（4）与下式等价：

$$ \boldsymbol{\theta}^{(\tau+1)}=(1-\lambda)\boldsymbol{\theta}^{(\tau)}-\eta\cdot \boldsymbol{M}^{(\tau)}\cdot \boldsymbol{g}^{(\tau)}\tag{6} $$

  比对可知，此时$\lambda\boldsymbol{\theta}^{(\tau)}=\eta\lambda'\cdot\boldsymbol{M}^{(\tau)}\cdot \boldsymbol{\theta}^{(\tau)}$，由于$\boldsymbol{M}\neq k\boldsymbol{I}$，则该等式不可能成立，因此在 自适应算法中，L2正则化与权重衰减不等价！ 也即以下两种算法是不等价的：

解耦权重衰减

  既然$L_2$正则与权重衰减在自适应算法中不等价，那么一个自然的问题是：究竟谁更有效？对于自适应算法，由于其使用梯度的二阶矩进行梯度缩放，所以带$L_2$正则的自适应算法迭代式可化为：

$$ \begin{align} \boldsymbol{\theta}^{(\tau+1)}&= \boldsymbol{\theta}^{(\tau)} -\eta\cdot \boldsymbol{M}^{(\tau)}\cdot \boldsymbol{g}^{(\tau)}-\eta\lambda'\cdot \boldsymbol{M}^{(\tau)}\cdot \boldsymbol{\theta}^{(\tau)}\\ &\approx \boldsymbol{\theta}^{(\tau)} -\eta\cdot \boldsymbol{M}^{(\tau)}\cdot \boldsymbol{g}^{(\tau)}-\eta\lambda'\cdot \underbrace{\frac{1}{\|\boldsymbol{\theta}^{(\tau)}\|}\cdot \boldsymbol{\theta}^{(\tau)}}_{\text{sign}(\boldsymbol{\theta}^{(\tau)})} \end{align} \tag{7} $$

此时$L_2$正则的作用约等于往优化过程里边加入$-\eta\lambda'\cdot\text{sign}(\boldsymbol{\theta}^{(\tau)})$而不是$-\eta\lambda'\cdot\boldsymbol{\theta}^{(\tau)}$，也就是说每个元素的惩罚都很均匀，而不是绝对值更大的元素惩罚更大，这部分抵消了$L_2$正则的作用，所以理论上而言，对于自适应方法权重衰减的效果应该是由于$L_2$正则的。那么有没有实验结果论证呢？文中最重要的结果如下：

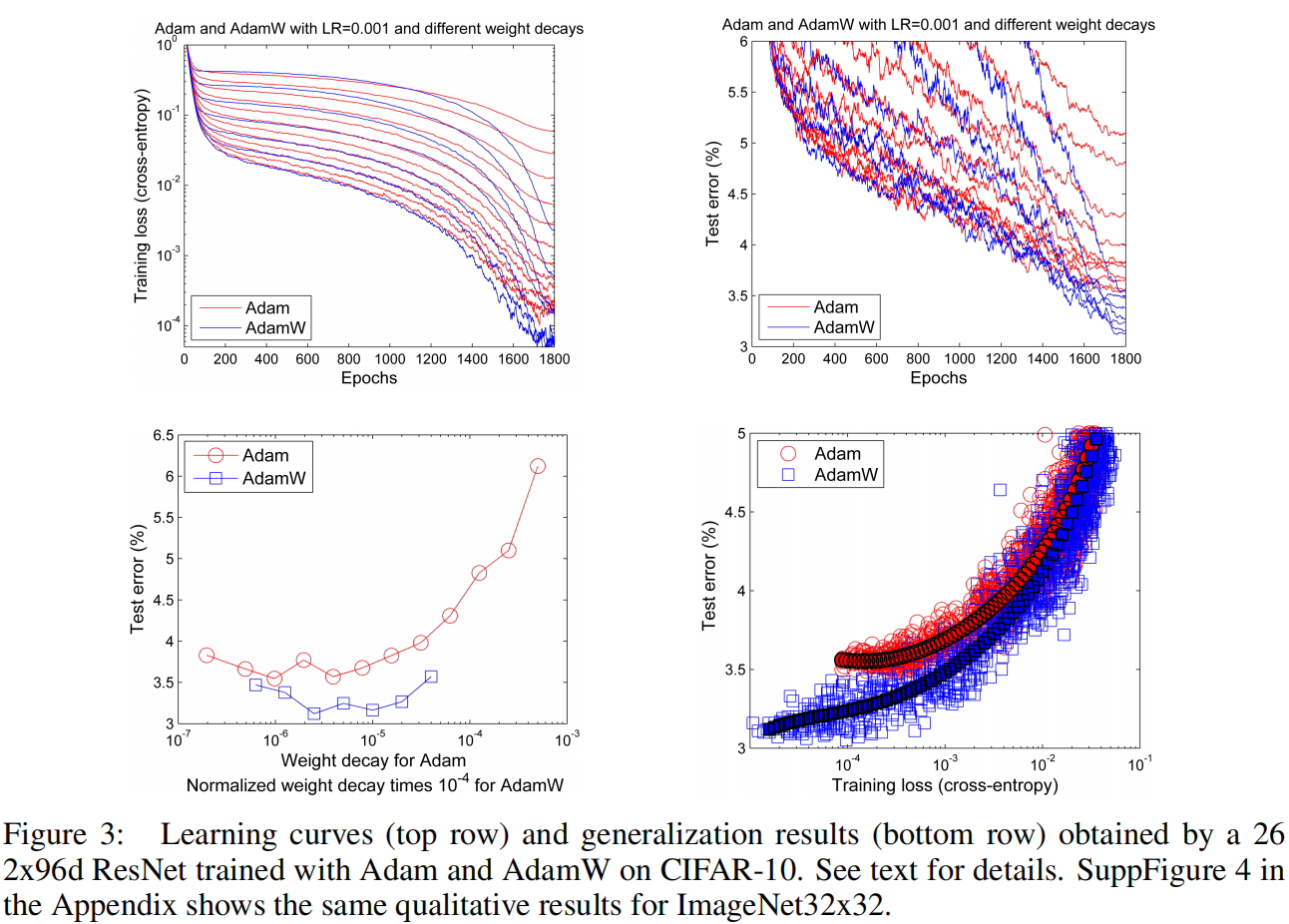
  可见解耦权重衰减后的Adam（AdamW）大概降低了15%左右的测试误差。文中还有一些其他的结果，都证明了Adam+权重衰减优于Adam+$L_2$正则。

References

1. 理解机器学习中的 L2 正则化
2. Comparing biases for minimal network construction with back-propagation，Stephen Jos´e Hanson and Lorien Y Pratt，1st NeurIPS，1988
3. (AdamW) Decoupled Weight Decay Regularization，Ilya Loshchilov, Frank Hutter，ICLR 2019