前言
本文介绍引入符号函数的算法SignSGD与SignUM。
基本形式
关于引入符号,其实说来形式非常简单,我们以最简单的SGD为例:
$$ \text{SGD}:\boldsymbol{\theta}^{(\tau)}=\boldsymbol{\theta}^{(\tau-1)}-\eta^{(\tau)}\cdot\boldsymbol{g}^{(\tau)}\tag{1} $$
引入符号函数就是在更新向量$\boldsymbol{g}^{(\tau)}$外套一个符号算子:
$$ \text{sign}(x)= \begin{cases} 1&, x>0\\ -1&,x<0 \end{cases} $$
则SignSGD的基本形式为:
$$ \text{SignSGD}:\boldsymbol{\theta}^{(\tau)}=\boldsymbol{\theta}^{(\tau-1)}-\eta^{(\tau)}\cdot\text{sign}(\boldsymbol{g}^{(\tau)})\tag{2} $$
当然这里的sign算子是element-wise的。我们也可以加上HB动量,就是SignUM算法:
$$ \begin{equation}\text{SignUM}:=\left\{\begin{aligned} &\boldsymbol{m}^{(\tau)} = \beta \boldsymbol{m}^{(\tau-1)} + \left(1 - \beta\right) \boldsymbol{g}^{(\tau)} \\ &\boldsymbol{u}^{(\tau)} = \text{sign}\big(\boldsymbol{m}^{(\tau)}\big) \\ &\boldsymbol{\theta}^{(\tau)} = \boldsymbol{\theta}^{(\tau-1)} - \eta^{(\tau)}\cdot \boldsymbol{u}^{(\tau)} \end{aligned}\right.\end{equation} $$
相较于SGD和HB,这样一个小小的改动究竟合不合理?此外有没有什么优势呢?
直观理解
0.从梯度下降说起
对于机器学习特别是深度学习而言,目前所有主流算法都是基于梯度的,而不论算法架构怎么改,梯度真正有用的其实是方向而非大小,所以只保留更新方向是合理的。
1.节省通信成本
符号函数可以看做一个二值量化的过程。在分布式机器学习中,计算端得到的梯度先经sign处理后,传输给服务器时就可以用INT8而不是用FLOAT32,这样便可以降低分布式计算中的传输成本。事实上,这正是SignSGD的设计初衷。
2.自适应方向
我们回顾一下Adam的参数迭代式:
$$ \text{Adam w/o bias correction}:\boldsymbol{\theta}^{(\tau)}=\boldsymbol{\theta}^{(\tau-1)}-\eta^{(\tau)}\cdot\frac{\boldsymbol{m}^{(\tau)}}{\sqrt{\boldsymbol{v}^{(\tau)}}}\tag{4} $$
其中分子分母分别是梯度一阶矩和二阶原点矩的估计,具体实现就是分别对梯度和梯度的平方取EMA(分母还要开方)。在Adam的文章中,作者并没有给出这么做比较理论的解释,所谓信噪比的观点也比较无趣。而直到17年,一篇ICML2018上与SignSGD同时期的工作给出了一个更为深刻的视角:
在浮点数的意义下不妨假设$m^{(\tau)}_i\neq 0$,有:
$$ \frac{\boldsymbol{m}^{(\tau)}}{\sqrt{\boldsymbol{v}^{(\tau)}}}=\frac{\text{sign}(\boldsymbol{m}^{(\tau)})}{\sqrt{\frac{\boldsymbol{v}^{(\tau)}}{\left(\boldsymbol{m}^{(\tau)}\right)^2}}}=\frac{\text{sign}(\boldsymbol{m}^{(\tau)})}{\sqrt{1+\frac{\boldsymbol{v}^{(\tau)}-\left(\boldsymbol{m}^{(\tau)}\right)^2}{\left(\boldsymbol{m}^{(\tau)}\right)^2}}}\tag{5} $$
其中分母是一个无量纲量,它与全局学习率$\eta$共同决定了更新的步长;而真正更新的方向仅由$\text{sign}(\boldsymbol{m}^{(\tau)})$决定。因此 自适应 算法可以拆解为两个部分: 自适应方向 与 自适应步长,后者在Dissecting Adam中称为variance adaptation。那么现在问题来了,究竟哪个方面才是Adam的精髓呢?Dissecting Adam与今年ICLR 2023上的一篇文章:
通过大量的实验说明了一个非常重要的结论:
有图有真相:(其中M-SSD就是SignUM)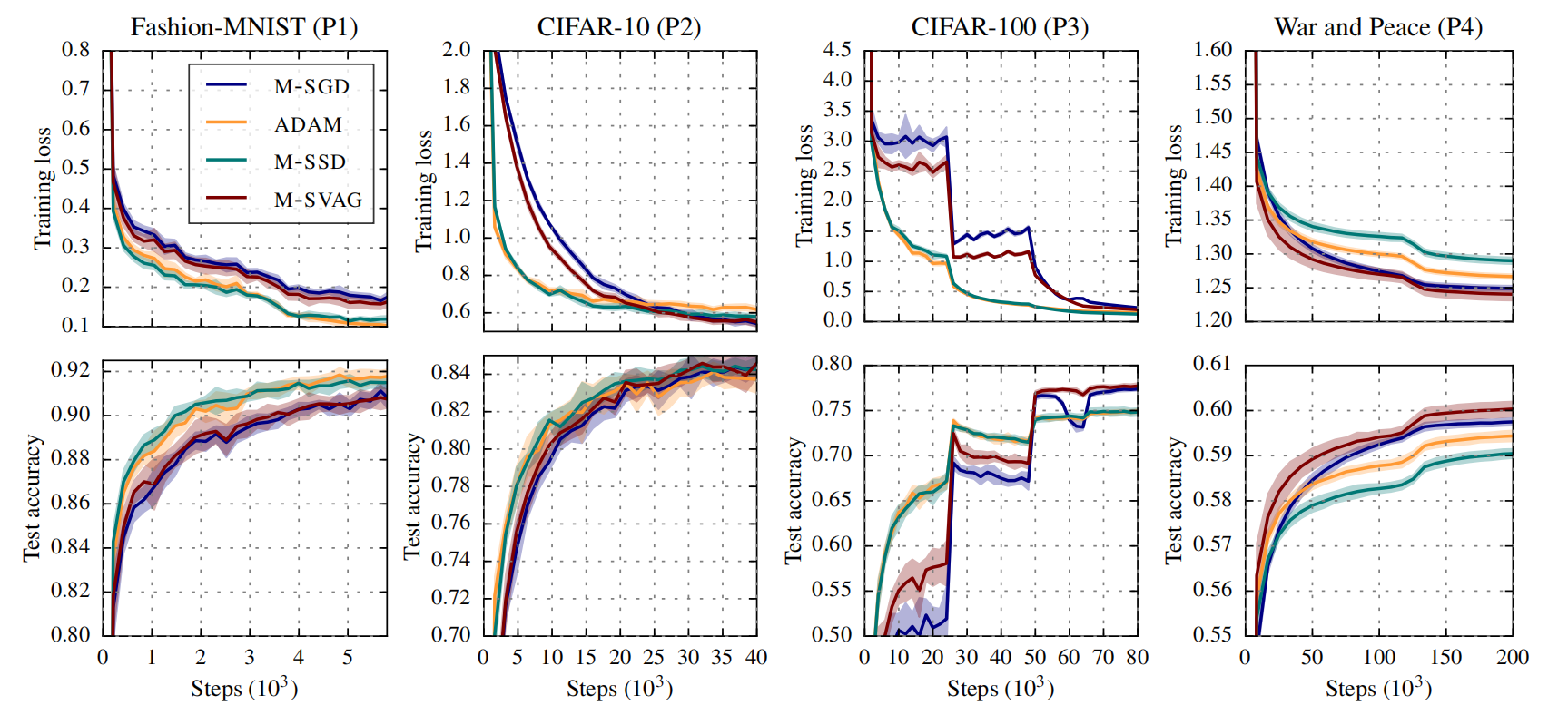
进而我们可以得出Dissecting Adam的一个核心结论:
We have argued that ADAM combines two components: taking signs and variance adaptation. Our experiments show that the sign aspect is by far the dominant one.
这样启示我们仅用符号函数与动量来构建更新量的想法是可行的。
3.速度与显存
对比SignUM与Adam:
$$ \begin{equation}\text{Adam}:=\left\{\begin{aligned} &\boldsymbol{m}^{(\tau)} = \beta_1 \boldsymbol{m}^{(\tau-1)} + \left(1 - \beta_1\right) \boldsymbol{g}^{(\tau)}\\ &\boldsymbol{v}^{(\tau)} = \beta_2 \boldsymbol{v}^{(\tau-1)} + \left(1 - \beta_2\right) \left(\boldsymbol{g}^{(\tau)}\right)^2\\ &\hat{\boldsymbol{m}}^{(\tau)} = \boldsymbol{m}^{(\tau)}\left/\left(1 - \beta_1^\tau\right)\right.\\ &\hat{\boldsymbol{v}}^{(\tau)} = \boldsymbol{v}^{(\tau)}\left/\left(1 - \beta_2^\tau\right)\right.\\ &\boldsymbol{u}^{(\tau)} =\hat{\boldsymbol{m}}^{(\tau)}\left/\left(\sqrt{\hat{\boldsymbol{v}}^{(\tau)}} + \varepsilon\right)\right.\\ &\boldsymbol{\theta}^{(\tau)} = \boldsymbol{\theta}^{(\tau-1)} - \eta^{(\tau)}\boldsymbol{u}^{(\tau)} \end{aligned}\right.\end{equation}\tag{6} $$
结果很明显,SignUM相比Adam参数更少(少了个$\varepsilon$),少缓存了一组参数$\boldsymbol{v}^{(\tau)}$(所以更省显存),并且去掉了Adam更新过程中计算量大的除法和开根号运算(所以更快)。
综合上述的理论与实践分析,我们可以认为用符号函数的框架:
$$ \text{Sign based Adaptive Methods}:\boldsymbol{\theta}^{(\tau)}=\boldsymbol{\theta}^{(\tau-1)}-\eta^{(\tau)}\cdot\text{sign}(\boldsymbol{u}^{(\tau)}))\tag{7} $$
来代替现有的自适应算法框架:
$$ \text{Adaptive Methods}:\boldsymbol{\theta}^{(\tau)}=\boldsymbol{\theta}^{(\tau-1)}-\eta^{(\tau)}\cdot\frac{\boldsymbol{m}^{(\tau)}}{\boldsymbol{v}^{(\tau)}}\tag{8} $$
是合理的。事实上Dissecting Adam正是基于这一点将现有的自适应算法都称为Stochastic Sign Descent,本文出于提出的时间顺序还是将符号函数自适应算法归纳为Adam类之外的一类。
代码实现
下面我们介绍一下SignSGD和SignUM的PyTorch实现。对于SignSGD则很简单,取个符号函数就可以了:
class signSGD(Optimizer):
def __init__(self, params, lr=0.01):
defaults = dict(lr=lr)
super(signSGD, self).__init__(params, defaults)
def step(self, closure=None):
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
# take sign of gradient
grad = torch.sign(p.grad)
# make update
p.data -= group['lr'] * grad对于SignUM而言则需要缓存一下一阶矩:
class signUM(Optimizer):
def __init__(self, params, lr=0.01, momentum=0):
defaults = dict(lr=lr, momentum=momentum)
super(signUM, self).__init__(params, defaults)
def __setstate__(self, state):
super(signUM, self).__setstate__(state)
def step(self):
for group in self.param_groups:
for p in group['params']:
if p.grad is None:
continue
grad = p.grad.data
state = self.state[p]
# State initialization
if len(state) == 0:
state['step'] = 0
# Exponential moving average of gradient values
state['exp_avg'] = torch.zeros_like(p.data, memory_format=torch.preserve_format)
momentum = group['momentum']
exp_avg = state['exp_avg']
state['step'] += 1
# update EMA of gradient
exp_avg.mul_(momentum).add_(grad, alpha=1 - momentum)
# take sign of gradient (or EMA of gradient)
update = torch.sign(exp_avg)
# make update
p.data.add_(update, alpha=-group["lr"])一个细节
可能有的读者会有疑问,对于0取符号后仍然是0,这会不会对训练产生什么影响呢?事实上SignSGD的作者考虑到了这样一个问题,并且在ResNet+CIFAR10上实验比较了 sign(0)->0 与随机将符号后的0变为±1的 sign(0)->±1,结果如下:
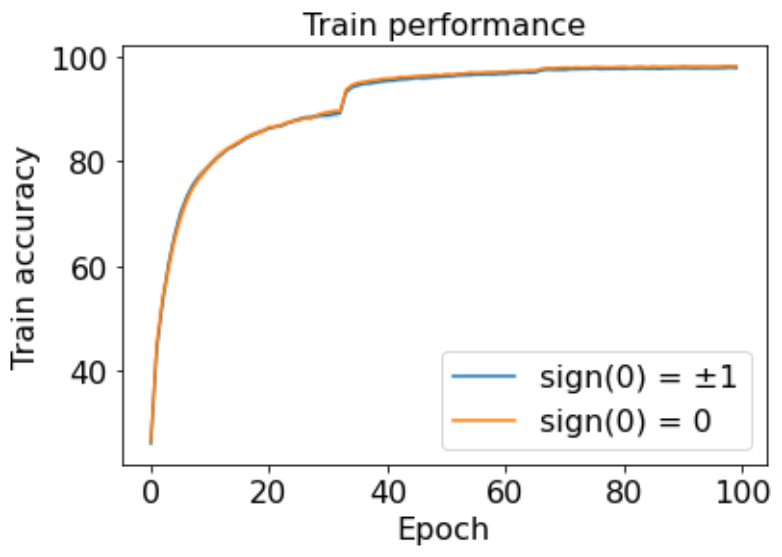
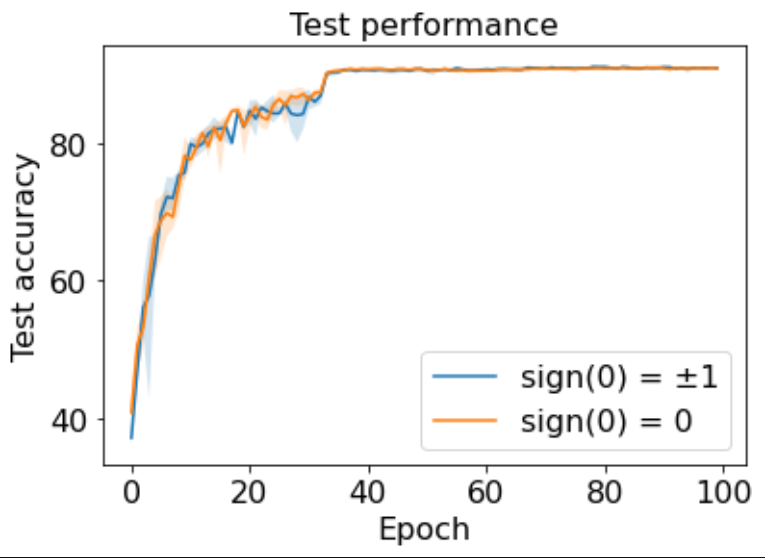
结果二者的区别微乎其微,这也说明现有实现是合理的,不用考虑0的情况。
References
- (SignSGD) SignSGD: Compressed Optimisation for Non-Convex Problems,Jeremy Bernstein, Yu-Xiang Wang, Kamyar Azizzadenesheli, Anima Anandkumar,ICML 2018 [[ICML PDF]](http://proceedings.mlr.press/v80/bernstein18a/bernstein18a.pdf) [[Newest Version PDF]](https://arxiv.org/pdf/1802.04434.pdf) [[Official PyTorch Implementation]](https://github.com/jxbz/signSGD)
- Dissecting Adam: The Sign, Magnitude and Variance of Stochastic Gradients,Lukas Balles, Philipp Hennig,ICML 2018,2017 [[ICML PDF]](http://proceedings.mlr.press/v80/balles18a/balles18a.pdf) [[Newest Version PDF]](https://arxiv.org/pdf/1705.07774.pdf)
- Noise Is Not the Main Factor Behind the Gap Between Sgd and Adam on Transformers, But Sign Descent Might Be,Frederik Kunstner, Jacques Chen, J. Wilder Lavington, Mark Schmidt,ICLR 2023,2023 [[ICLR PDF]](https://openreview.net/pdf?id=a65YK0cqH8g)
