优化器九：自适应算法与AdaGrad

前言

  本文我们介绍AdaGrad算法。

自适应算法与AdaGrad

  我们知道，所有优化方法都是迭代算法，其可以表示为：

$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}+\eta^{(\tau)}\cdot \boldsymbol{d}^{(\tau)}\tag{1} $$

  在之前的文章中，我们介绍了SGD、MSGD、SUM等算法，从本质上而言，这些算法都是从优化方向$\boldsymbol{d}^{(\tau)}$的角度进行改进。对于步长（或称为学习率）我们通常取为常数或多项式衰减。但是实际中手动调参非常痛苦，而且对于神经网络这种高维的非凸函数，各层乃至各维对于学习率的敏感程度是不同的，具体而言在训练过程中，不同参数的改变程度不同。对于某些参数，可能经过大量迭代更新，已经优化到了极小值附近，不需要再进行较大程度的改变。但是有些参数前期改变较小，经过许多次更新后其梯度分量才变大，需要继续大幅更新参数。沿着这个思路，John Duchi等在2011年提出了AdaGrad（Adaptive Gradient Algorithm）算法，去掉一维搜索后应用于工程实践中的算法即为：

$$ \theta^{(\tau+1)}_i=\theta^{(\tau)}_i-\frac{\eta}{\sqrt{\sum\limits_{k=1}^{\tau}\left(g^{(k)}_i \right)^2+\varepsilon}}\cdot g^{(\tau)}_i\tag{2} $$

其中$x_i$表示向量$\boldsymbol{x}$的第$i$维分量，$\varepsilon>0$是避免分母为零的调节项，一般取$10^{-8}$左右的量级。本质上而言，AdaGrad是为每一个参数分配了一个参考了历史更新信息的学习率：

$$ \eta^{(\tau)}_i =\frac{\eta}{\sqrt{\sum\limits_{k=1}^{\tau}\left(g^{(k)}_i \right)^2+\varepsilon}}\tag{3} $$

  引入Hadamard积算子$\odot$，则我们可以把（2）写成向量的形式：

$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\frac{\eta}{\sqrt{\varepsilon\boldsymbol{1}+\sum\limits_{k=1}^{\tau}\boldsymbol{g}^{(k)} \odot\boldsymbol{g}^{(k)} }}\odot \boldsymbol{g}^{(\tau)}\tag{4} $$

AdaGrad的理论分析

  AdaGrad的收敛速度如何呢？为了表述简便，设$\boldsymbol{\theta}\in\mathbb{R}^{P}$。首先我们来看凸函数的情况。

1.$L$-光滑+凸

  设$\mathcal L\in \mathcal F_{0,L}^{1,1}$，由凸性：

$$ \mathcal L(\boldsymbol{\theta}^{(\tau)})-\mathcal L(\boldsymbol{\theta}^*)\leq \left\langle \boldsymbol{g}^{(\tau)} ,\boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^* \right\rangle=\sum_{i=1}^P g^{(\tau)}_i \left(\theta^{(\tau)}_i-\theta^*_i \right)\tag{5} $$

  结合（3）（4），对于第$i$个分量我们有：（为了分析起来方便我们去掉$\varepsilon$）

$$ \theta^{(\tau+1)}_i=\theta^{(\tau)}_i-\eta^{(\tau)}_i\cdot g^{(\tau)}_i,\eta^{(\tau)}_i=\frac{\eta}{\sqrt{\sum\limits_{k=1}^{\tau}\left(g^{(k)}_i \right)^2}} \tag{6} $$

在（6）两边减去$\theta^*_i$再平方，我们有：

$$ g^{(\tau)}_i\left(\theta^{(\tau)}_i-\theta^*_i \right)=\frac{1}{2\eta^{(\tau)}_i}\left[\left(\theta^{(\tau)}_i-\theta^*_i \right)^2- \left(\theta^{(\tau+1)}_i-\theta^*_i \right)^2\right]+\frac12 \eta^{(\tau)}_i \left(g^{(\tau)}_i \right)^2\tag{7} $$

  我们假设变量每一维离最优解不会太远：$\mathbb{E}\left[\left(\theta^{(\tau)}_i-\theta^*_i \right)^2\right]\leq D_i^2$，随机梯度每一维的平方有界：$\mathbb{E}\left[\left(g^{(\tau)}_i \right)^2\right]\leq G_i^2$，则由（7）我们有：

$$ \begin{align} \sum_{k=1}^\tau \mathbb{E}\left[g^{(k)}_i\left(\theta^{(k)}_i-\theta^*_i \right)\right]&\leq \mathbb{E}\left[\frac{D_i^2}{2\eta^{(\tau)}_i}\right]+\sum_{k=1}^\tau \mathbb{E}\left[\frac{\eta_i^{(k)}}{2}\left(g^{(k)}_i \right)^2\right]\\ &=\frac{D_i^2}{2\eta}\sqrt{\sum\limits_{k=1}^{\tau}\mathbb{E}\left[\left(g^{(k)}_i \right)^2\right]}+\frac\eta2\sum_{k=1}^\tau \mathbb{E}\bigg[\frac{\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\left(g^{(s)}_i\right)^2}}\bigg]&代入\eta^{(\tau)}_i\\ &\leq \frac{D_i^2G_i}{2\eta}\sqrt{\tau}+\frac\eta2\underbrace{\sum_{k=1}^\tau\mathbb{E}\bigg[ \frac{\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\left(g^{(s)}_i \right)^2}}\bigg]}_{S}\tag{8} \end{align} $$

  把$S$单独拿出来分析，我们有：

$$ \begin{align} \sum_{k=1}^\tau\mathbb{E}\bigg[ \frac{\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\left(g^{(s)}_i \right)^2}}\bigg]&= \sum_{k=1}^\tau \mathbb{E}\bigg[\frac{2\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\left(g^{(s)}_i \right)^2}+\sqrt{\sum\limits_{s=1}^{k}\left(g^{(s)}_i \right)^2}}\bigg]\\ &\leq \mathbb{E}\bigg[\frac{\left(g^{(1)}_i \right)^2}{\sqrt{\left(g^{(1)}_i \right)^2}}\bigg]+\sum_{k=2}^\tau \mathbb{E}\bigg[\frac{2\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\left(g^{(s)}_i \right)^2}+\sqrt{\sum\limits_{s=1}^{\color{Red}k-1}\left(g^{(s)}_i \right)^2}}\bigg]\\ &=\mathbb{E}\bigg[\sqrt{\left(g^{(1)}_i \right)^2}\bigg]+\sum_{k=2}^\tau \left(2\sqrt{\sum\limits_{s=1}^{k}\mathbb{E}\bigg[\left(g^{(s)}_i \right)^2\bigg]}-2\sqrt{\sum\limits_{s=1}^{k-1}\mathbb{E}\bigg[\left(g^{(s)}_i \right)^2\bigg]} \right)\\ &= 2\sqrt{\sum\limits_{s=1}^{\tau}\mathbb{E}\bigg[\left(g^{(s)}_i \right)^2\bigg]}-\mathbb{E}\left[\sqrt{\left(g^{(1)}_i \right)^2}\right]\leq 2G_i\sqrt{\tau}\tag{9} \end{align} $$

  此外，我们考察迭代序列$\{\boldsymbol{\theta}^{(\tau)}\}$的Cesáro平均：

$$ \tilde{\boldsymbol{\theta}}^{(\tau)}=\frac{1}{\tau}\sum_{k=1}^\tau \boldsymbol{\theta}^{(k)}\tag{10} $$

其对应的优化误差记为：$\tilde{\epsilon}(\tau)=\mathcal L(\tilde{\boldsymbol{\theta}}^{(\tau)})-\mathcal L(\boldsymbol{\theta^*})$。考虑算子：$\mathbb{E}[\cdot]=\mathbb{E}_{\boldsymbol{\xi}_{i_1}}\cdot\mathbb{E}_{\boldsymbol{\xi}_{i_\tau}}[\cdot]$，我们有：

$$ \begin{align} \mathbb{E}[\tilde{\epsilon}(\tau)]&\leq \frac{1}\tau\sum_{k=1}^\tau \mathbb{E}[\epsilon(k)]&Jensen不等式\\ &\leq \frac1\tau\sum_{i=1}^P\sum_{k=1}^\tau g^{(k)}_i \left(\theta^{(k)}_i-\theta^*_i \right) & 代入(5)\\ & \leq \sum_{i=1}^P\left[\frac{D_i^2}{2\eta}+\eta \right]\frac{G_i}{\sqrt{\tau}}&代入(8)(9) \end{align} $$

  所以，我们在凸的情况下有如下定理：

定理1：

  设$\mathcal L\in\mathcal F_{0,L}^{1,1}$，且：

$$ \mathbb{E}\left[\left(\theta^{(\tau)}_i-\theta^*_i \right)^2\right]\leq D_i^2,\mathbb{E}\left[\left(g^{(\tau)}_i \right)^2\right]\leq G_i^2 $$

则：

$$ \mathbb{E}[\tilde{\epsilon}(\tau)]\leq \sum_{i=1}^P\left[\frac{D_i^2}{2\eta}+\eta \right]\frac{G_i}{\sqrt{\tau}}=O(\frac{1}{\sqrt\tau}) $$

这与SGD的收敛速度阶数是相同的。

1.$L$-光滑

  对于非凸的情况，参考资料3给出了收敛速度：$\mathbb{E}[\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)})\|^2]\leq O(\frac{\ln \tau}{\sqrt\tau})$，这里就不重复造轮子了。参考资料4有类似的结果。这与SGD也是同阶的。

AdaGrad的优劣

  作为第一种自适应方法，AdaGrad 算法的一个最明显的优点是不需要人工调整学习率。Dean 等人发现AdaGrad能显著提高SGD的
鲁棒性，并将其用于谷歌的大型神经网络训练（见参考资料5），如下图：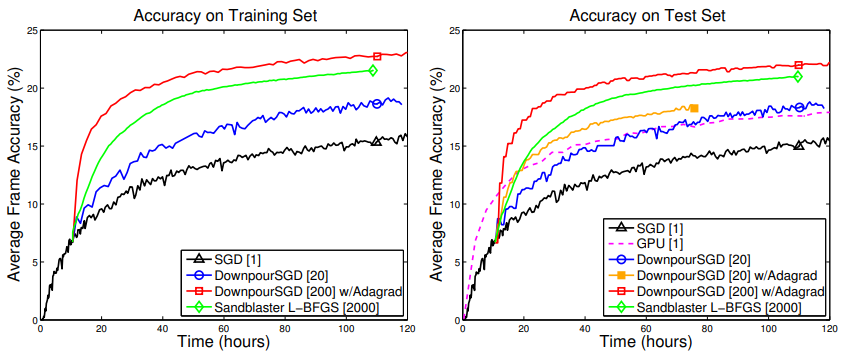

  此外著名的GloVe词向量也是用AdaGrad训练的，因为低频词比高频词需要更大的更新。
  而AdaGrad的缺点也是很显然的，历史梯度无节制地累加导致了学习率快速衰减至一个极小的数, 这使得训练后期优化效率很低。

AdaGrad的PyTorch实现

  PyTorch中已经含有了AdaGrad的实现，它是一种multi-stage的形式：

$$ \begin{align} \boldsymbol{v}^{(\tau)}&=\boldsymbol{v}^{(\tau-1)}+\boldsymbol{g}^{(\tau)}\odot\boldsymbol{g}^{(\tau)}\\ \boldsymbol{\theta}^{(\tau+1)}&=\boldsymbol{\theta}^{(\tau)}-\frac{\eta}{\sqrt{\boldsymbol{v}^{(\tau)}}+\varepsilon}\odot\boldsymbol{g}^{(\tau)} \end{align} $$

其中$\boldsymbol{v}^{(0)}=\boldsymbol{0}$。这种实现方式避免了存储$\tau$时刻之前的所有梯度信息。此外在实现时注意element-wise的平方我们可以使用addcmul方法，更快。加法与开方也要注意是否是原地操作。

class AdaGrad(Optimizer):
    def __init__(self, params, lr=1e-3, eps=1e-10):
        if not 0.0 <= lr:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if not 0.0 <= eps:
            raise ValueError("Invalid epsilon value: {}".format(eps))
        
        defaults = dict(lr=lr, eps=eps)
        super(AdaGrad, self).__init__(params, defaults)
        
        for group in self.param_groups:
            for p in group['params']:
                state = self.state[p]
                state['step'] = 0
                state['sum'] = torch.full_like(p, 0, memory_format=torch.preserve_format)

    @torch.no_grad()
    def step(self):
        for group in self.param_groups:
            params_with_grad = []
            grads = []
            state_sums = []
        
            for p in group['params']:
                if p.grad is not None:
                    params_with_grad.append(p)
                    grads.append(p.grad)
                    state = self.state[p]
                    state_sums.append(state['sum'])

            for (param, grad, state_sum) in zip(params_with_grad, grads, state_sums):
                state_sum.addcmul_(grad, grad, value=1)
                std = state_sum.sqrt().add_(group['eps'])
                param.addcdiv_(grad, std, value=-group['lr'])

AdaGrad的变种

1. AdaGrad-Norm

  参考资料7提出了一种AdaGrad的变种算法：

$$ \begin{align} v^{(\tau)}&=v^{(\tau-1)}+{\color{Red}\|\boldsymbol{g}^{(\tau)}\|^2}\\ \boldsymbol{\theta}^{(\tau+1)}&=\boldsymbol{\theta}^{(\tau)}-\frac{\eta}{\sqrt{v^{(\tau)}}+\varepsilon}\cdot\boldsymbol{g}^{(\tau)} \end{align} $$

其中$v^{(0)}=0$。也就是说累计的并不是梯度而是梯度范数，同样是参考了历史梯度信息但舍弃了element-wise的方式。在泛化能力能方面较AdaGrad更好，但是范数的计算引入了额外的计算量，而且收敛速度上没有阶数的提升。

2.Weighted-AdaGrad

  一个更为自然的思路是为累加的每一时刻的随机梯度赋予一权重，也即：

$$ \begin{align} \boldsymbol v^{(\tau)}&=\boldsymbol v^{(\tau-1)}+{\color{Red}\beta(\tau)}\cdot\boldsymbol{g}^{(\tau)}\odot \boldsymbol{g}^{(\tau)} \\ \boldsymbol{\theta}^{(\tau+1)}&=\boldsymbol{\theta}^{(\tau)}-\underbrace{\frac{\color{Red}\beta(\tau)}{\sqrt{\boldsymbol v^{(\tau)}}}}_{\boldsymbol{\eta}^{(\tau)}}\cdot\boldsymbol{g}^{(\tau)} \end{align} $$

鉴于AdaGrad学习率衰减太快导致对后期梯度不敏感的缺陷，我们取权重序列为一个单增序列：$\beta(1)\leq \beta(2)\leq \cdots$。我们简单研究一下它在凸情况下的表现。此时（7）式可以复用，对于（8）式我们可以将其改为：

$$ \begin{align} \sum_{k=1}^\tau \mathbb{E}\left[g^{(k)}_i\left(\theta^{(k)}_i-\theta^*_i \right)\right]&\leq \mathbb{E}\left[\frac{D_i^2}{2\eta^{(\tau)}_i}\right]+\sum_{k=1}^\tau \mathbb{E}\left[\frac{\eta_i^{(k)}}{2}\left(g^{(k)}_i \right)^2\right]\\ &=\frac{D_i^2}{2\beta(\tau)}\underbrace{\sqrt{\sum\limits_{k=1}^{\tau}\beta(k)\mathbb{E}\left[\left(g^{(k)}_i \right)^2\right]}}_{A_1}+\frac12\underbrace{\sum_{k=1}^\tau \mathbb{E}\bigg[\frac{\beta(k)\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\beta(s)\left(g^{(s)}_i\right)^2}}\bigg]}_{A_2}\tag{11} \end{align} $$

  对于$A_1$我们有：$A_1\leq G_i\sqrt{\sum\limits_{k=1}^\tau \beta(k)}$，对于$A_2$，类似于（9）式，我们有：

$$ \begin{align} \sum_{k=1}^\tau \mathbb{E}\bigg[\frac{\beta(k)\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\beta(s)\left(g^{(s)}_i\right)^2}}\bigg]&=\sum_{k=1}^\tau \mathbb{E}\bigg[\frac{2\beta(k)\left(g^{(k)}_i \right)^2}{\sqrt{\sum\limits_{s=1}^{k}\beta(s)\left(g^{(s)}_i\right)^2}+\sqrt{\sum\limits_{s=1}^{k}\beta(s)\left(g^{(s)}_i\right)^2}}\bigg]\\ &\leq \mathbb{E}\left[\sqrt{\beta(1)\left(g^{(1)}_i \right)^2}\right]+\sum_{k=2}^\tau \left(2\sqrt{\sum\limits_{s=1}^{k}\beta(s)\mathbb{E}\bigg[\left(g^{(s)}_i \right)^2\bigg]}-2\sqrt{\sum\limits_{s=1}^{k-1}\beta(s)\mathbb{E}\bigg[\left(g^{(s)}_i \right)^2\bigg]} \right)\\ &\leq 2G_i\sqrt{\sum\limits_{k=1}^\tau \beta(k)}\tag{12} \end{align} $$

  所以：

$$ \begin{align} \mathbb{E}[\tilde{\epsilon}(\tau)]&\leq \frac{1}\tau\sum_{k=1}^\tau \mathbb{E}[\epsilon(k)]&Jensen不等式\\ &\leq \frac1\tau\sum_{i=1}^P\sum_{k=1}^\tau g^{(k)}_i \left(\theta^{(k)}_i-\theta^*_i \right) & 代入(5)\\ & \leq \sum_{i=1}^P\left[\frac{D_i^2}{2\beta(\tau)}+1 \right]G_i\cdot\frac{\sqrt{\sum\limits_{k=1}^\tau \beta(k)}}{\tau} &代入(11)(12) \end{align} $$

  当$\beta(\tau)\equiv 1$时，显然Weighted-AdaGrad退化成了$\eta=1$时的AdaGrad，而当$\beta(\tau)=\beta\sqrt{\tau}$时，$\mathbb{E}[\tilde{\epsilon}(\tau)]\leq O(\tau^{-\frac 14})$；当$\beta(\tau)=\beta\log\tau$时，$\mathbb{E}[\tilde{\epsilon}(\tau)]\leq O(\sqrt{\frac{\log \tau}{\tau}})$。所以Weighted-AdaGrad虽然能够使得新样本权重增加，学习率衰减变慢，但理论上的收敛速度慢于AdaGrad，而且很容易溢出。
  事实上这种给每个时刻累加的随机梯度一个权重的思路是正确的，但是具体操作不应该是新梯度提权，而应该是旧梯度降权。如果权重以指数速度衰减，则即是RMSProp算法，我们将在下一篇文章中介绍。

References

1. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization，John Duchi et al，Journal of machine learning research（JMLR），2011
2. 【科研喂饭】深度学习算法收敛性证明之Adagrad
3. A simple convergence proof of adam and adagrad，Alexandre Défossez et al，arXiv preprint arXiv:2003.02395，2020
4. **On the Convergence of Adaptive Gradient Methods for
   Nonconvex Optimization*，Dongruo Zhou et al*，arXiv preprint arXiv:1808.05671，2018
5. Large scale distributed deep networks，Jeffrey Dean，Advances in Neural Information Processing Systems（NIPS），2012
6. https://pytorch.org/docs/stable/generated/torch.optim.Adagrad.html#torch.optim.Adagrad
7. **AdaGrad stepsizes: Sharp convergence over nonconvex
   landscapes*，Rachel Ward*，The Journal of Machine Learning Research（JMLR），2020