前言
本文介绍一个经典的基于动量的加速算法:Heavy-ball method。
一、回顾SGD
在之前的文章中:
我们介绍了SGD与Mini-Batch SGD:
$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta^{(\tau)} \cdot g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]}) \tag{1} $$
它相对于GD在计算效率上有显著提升,同时还具有一定的正则化效果。同时我们也分析了它的一些缺点。我们来看下面的两个例子。
考虑ERM问题:
$$ \min\mathcal{L}(\theta_1,\theta_2)=\frac{1}{N}\sum_{i=1}^N \xi_{[i]}^2\cdot l(\theta_1,\theta_2)\tag{2} $$
其中$\xi\sim N(\frac 12,\sigma^2)$。那么在期望的意义下,$\mathcal L$关于$\theta_1,\theta_2$的曲线即为$l$的曲线!这样我们便可以用ERM的观点去研究各种二元函数。首先我们取$l(\theta_1,\theta_2)=\theta_1^2-\theta_2^2$,考察在鞍点附近的性能:

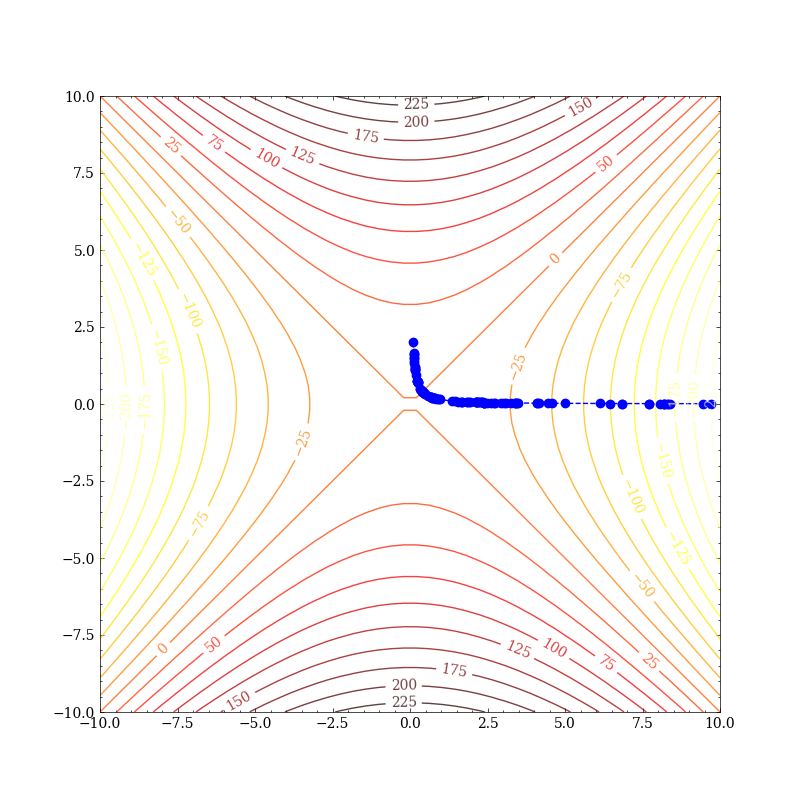
可以看出虽然SGD能逃离鞍点,但仍花费了很长的时间。我们再来看局部最小的情况。取:
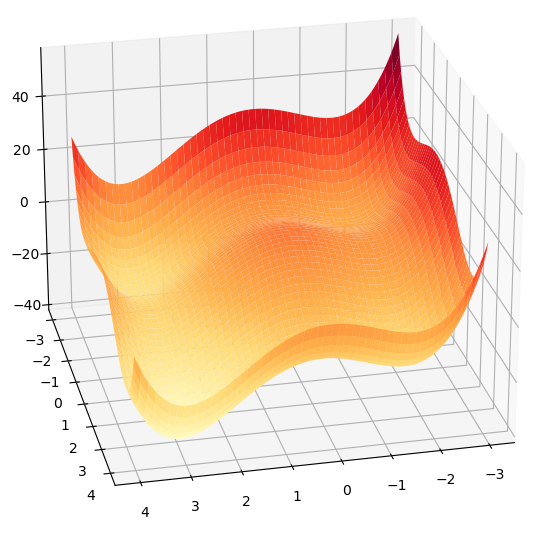
$$ \begin{align} l(\theta_1,\theta_2)&=(\theta_1 + 2) * (\theta_1 + 1) * (\theta_1 - 1) * (\theta_1 / 2 - 2)\\ &+(\theta_2 +2) * (\theta_2 + 1) * (\theta_2 - 1) * (\theta_2 / 2 - 2) \end{align} $$
其图像为:
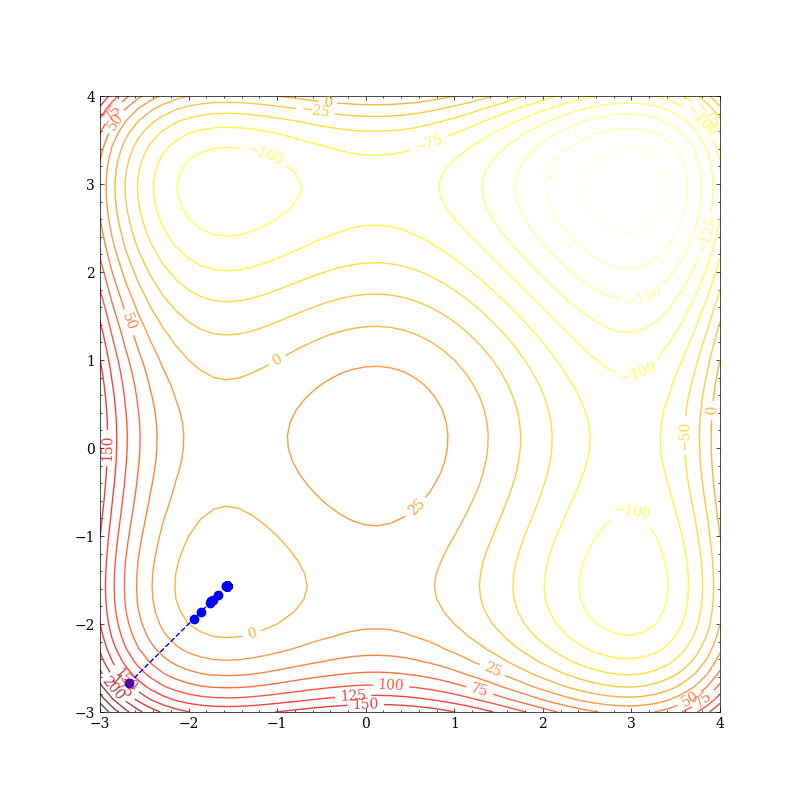
在学习率为0.01时,很容易便掉到了局部最优里:
我们再取$l$为罗森布洛克函数(Rosenbrock function):
$$ l(\theta_1,\theta_2)=(1-\theta_1)^2+100(\theta_2-\theta_1^2)^2 $$
容易知道,它具有全局最小值点$(1,1)$,而且有一个狭长的“峡谷”结构。我们将其取个对数(见右图,图源参考资料1)看得更加清楚:


我们从$(-2,2)$开始,使用SGD优化,会发现我们的参数一直在峡谷中震荡(前200次迭代):

如果我们把每个点的梯度按两个坐标轴方向分解(图源参考资料2):
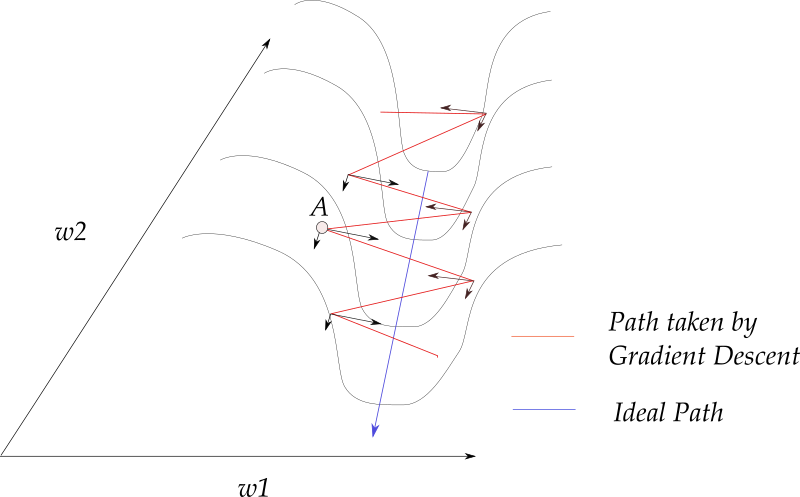
我们会发现,梯度的方向几乎垂直于峡谷的“长轴”(long axis),梯度下降方法在峡谷的“短轴”(short axis)方向上来回振荡,并且仅沿着峡谷的长轴非常缓慢的移动。这个问题在参考资料3中被称为病态曲率问题。
And if the only directions of significant decrease in f are ones of low curvature, the optimization may become too slow to be practical and even appear to halt altogether, creating the false impression of a local minimum.
那么我们能不能从SGD出发,设计一种改进算法来缓解上述的三个问题呢?
二、SGD+Momentum
Polyak在1964年将动量项引入SGD(参考资料4),即:
$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta^{(\tau)} \cdot g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})+\beta^{(\tau)}\cdot (\boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^{(\tau-1)}) \tag{3} $$
其中$\beta\in(0,1)$。我们将上式称为Heavy-ball method(HB)。为啥要叫这么奇怪的名字呢?我们在下一篇文章中会介绍到。
三、直观理解
HB相较于SGD看上去不就是加上了一个动量项$\beta^{(\tau)} (\boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^{(\tau-1)})$嘛,是怎么缓解我们上面提到的三个问题呢?
直观上而言,HB方法每一步迭代在进行梯度下降的同时,将更新的历史信息加入到参数更新上。更准确地而言,除了当前的随机梯度之外,还包含了历史梯度的指数平均:
$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta^{(\tau)}g(\boldsymbol{\theta}^{(\tau)},\boldsymbol{\xi}_{[i_\tau]})+\sum_{k=1}^{\tau} \eta^{(k-1)}\beta^{(\tau)}\cdots \beta^{(k)}g(\boldsymbol{\theta}^{(k-1)},\boldsymbol{\xi}_{[i_{k-1}]})\tag{4} $$
对于参数各维度曲率不一致的情况(例如上述的病态曲率问题),HB能够使得梯度下降在方向一致的维度上加速,在梯度震荡明显的维度上减速使得算法能更快地通过峡谷。
此外从训练的整体过程而言,训练的初期梯度的迭代方向基本都是一致的,动量加速法会加速参数收敛;在训练后期,梯度的迭代方向变化很大,很容易在最优值点附近震荡,动量加速法会起到减小更新的幅度,使得参数逐渐逼近最优值点。
所以,HB在鞍点、病态曲率问题上应该比SGD表现更好;而且收敛速度应该更快。那么理论上能否证明上述结论呢?
四、统一符号
首先我们统一一下记号,在之前的文章中记号有点不清晰,我们使用参考资料5中的表述,记满足$k$阶连续可微且其$p(\leq k)$阶导函数Lipschitz连续,即:
$$ \|f^{(p)}(\boldsymbol{x})-f^{(p)}(\boldsymbol{y}) \|\leq L\|\boldsymbol{x} -\boldsymbol{y}\| $$
的所有函数$f$构成的集合为$\mathcal C_{L}^{k,p}$,特别地,若$f\in\mathcal C^{1,1}_L$,则称$f$为Lipschitz光滑,简称$L$-光滑。若$f$是$k$阶连续可微的且$f$为$\mu$-强凸,则记$f\in\mathcal F_\mu^{k}$。我们结合上述两个条件,若$f$是$k$阶连续可微、其$p(\leq k)$阶导函数Lipschitz连续、$f$为$\mu$-强凸,则记$f\in\mathcal F_{\mu,L}^{k,p}$。特别地,当$\mu=0$时则为普通凸函数。
此外,在下文中我们简记随机梯度$g(\boldsymbol{\theta}^{(k-1)},\boldsymbol{\xi}_{[i_{k-1}]})$为$\boldsymbol{g}_{\tau}$。
五、HB+GD
加上动量项之后,理论分析的难度大了很多,所以哪怕HB方法提出了将近60年了,对于它的理论分析仍然是不太充分的。我们首先来热热身,首先来看将HB应用于Vanilla Gradient Descent的情况,也即:
$$ \boldsymbol{\theta}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}-\eta^{(\tau)} \cdot \nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)})+\beta^{(\tau)}\cdot (\boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^{(\tau-1)}) \tag{5} $$
我们复习一下GD的收敛性:
| 条件 | $\tau(\epsilon)$ | $\epsilon(\tau)$ | $\tau_S(\epsilon)$ | 收敛速度 |
|---|---|---|---|---|
| $\mathcal C^{1,1}_{L}$ | - | - | $\Omega(\frac 1 {\epsilon^2})$ | 次线性收敛 |
| $\mathcal F_{0,\mu}^{1,1}$ | $\Omega(\frac 1\epsilon)$ | $O(\frac{1}{\tau})$ | $\Omega(\frac 1 {\epsilon^2})$ | 次线性收敛 |
| $\mathcal F_{\mu,L}^{1,1}$ | $\Omega((\log \frac{1}{\epsilon})/\log \frac{\kappa}{\kappa-1})$ | $O\left((1-\kappa^{-1})^\tau \right)$ | $\Omega((\log \frac{1}{\epsilon^2})/\log \frac{\kappa}{\kappa-1})$ | 线性收敛 |
5.1:$L$-光滑+$\mu$-强凸
首先我们来看最好分析的$L$-光滑+$\mu$-强凸的情况。事实上Polyak在1964提出HB时就顺带证明了这种情况下的收敛性,见参考资料4的Section2,这里就不重复造轮子了。
定理1:
若$\mathcal L\in \mathcal F_{\mu,L}^{2,1}$,且:
$$ \eta^{(\tau)}\equiv \eta=\frac{4}{(\sqrt L+\sqrt m)^2},\ \beta^{(\tau)}\equiv\beta=\left( \frac{\sqrt \kappa-1}{\sqrt \kappa+1}\right)^2 $$
则:
$$ \|\boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^* \|^2\leq O\left(\left( \frac{\sqrt \kappa-1}{\sqrt \kappa+1}\right)^\tau \right)\tag{6} $$
容易知道,$\frac{\sqrt \kappa-1}{\sqrt \kappa+1}\leq 1-\kappa^{-1}$,当且仅当$\kappa=1$时取等号。所以,HB是要比GD收敛更快的,而且条件数越大收敛更快!
对于序列$\{\epsilon(\tau) \}$的分析,可见参考资料6的定理4,具体地:
定理2:
若$\mathcal L\in \mathcal F_{\mu,L}^{1,1}$,且:
$$ \eta^{(\tau)}\equiv \eta\in\left(0,\frac 2L \right),\ \beta^{(\tau)}\equiv\beta\in\left(0,\frac{\mu\eta}{4}+\frac 12\sqrt{\frac{\mu^2\eta^2}4+4(1-\frac{L\eta}{2})} \right) $$
则:
$$ \epsilon(\tau)\leq O(\rho^\tau),\ \rho\in(0,1) $$
$\rho$的具体表达很复杂,这里就不展开了,读者可以参阅原文。比较定理1、2,可见定理2对$\mathcal L$的条件更松,但是不能与GD比较收敛速度了。
5.2:$L$-光滑+凸
对于$L$-光滑+凸的情况,参考资料6的定理1给出了如下结论:
定理3:
若$\mathcal L\in \mathcal F_{0,L}^{1,1}$,且:
$$ \eta^{(\tau)}\equiv \eta\in\left(0,\frac {2(1-\beta)}{L} \right),\ \beta^{(\tau)}\equiv\beta\in(0, 1) $$
则:
$$ \mathcal L\left(\bar{\boldsymbol{\theta}}^{(\tau)}\right)-\mathcal L(\boldsymbol{\theta}^*) \leq\left\{\begin{array}{ll} \frac{\left\|\boldsymbol{\theta}^{(0)}-\boldsymbol{\theta}^*\right\|^{2}}{2\tau}\left(\frac{L \beta}{1-\beta}+\frac{1-\beta}{\eta}\right), & \text { if } \eta \in\left(0, \frac{1-\beta}{L}\right) \\ \frac{\left\|\boldsymbol{\theta}^{(0)}-\boldsymbol{\theta}^*\right\|^{2}}{2\tau\cdot(2(1-\beta)-\eta L)}\left(L \beta+\frac{(1-\beta)^{2}}{\eta}\right), & \text { if } \eta \in\left[\frac{1-\beta}{L}, \frac{2(1-\beta)}{L}\right) \end{array}\right. $$
其中:$\bar{\boldsymbol{\theta}}^{(\tau)}=\frac{1}{\tau}\sum_{k=1}^\tau \boldsymbol{\theta}^{(k)}$。显然,$\epsilon(\tau)\leq \mathcal L\left(\bar{\boldsymbol{\theta}}^{(\tau)}\right)-\mathcal L(\boldsymbol{\theta}^*)$,所以$\epsilon(\tau)\leq O(\frac{1}{\tau})$。
5.3:$L$-光滑
最后我们简要看一下非凸情况下的分析。参考资料7给出了收敛性:
定理4:
若$\mathcal L\in \mathcal C_{L}^{1,1}$,且:
$$ \eta^{(\tau)}\equiv \eta\in\left(0,\frac {2(1-\beta)}{L} \right),\ \beta^{(\tau)}\equiv\beta\in(0, 1) $$
则:
$$ \lim_{\tau\to\infty}\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)}) \|=0 $$
对于收敛速度,参考文献8证明了:
定理4:
若$\mathcal L\in \mathcal C_{L}^{1,1}$,且:
$$ \eta^{(\tau)}\equiv \eta\in\left(0,\frac {2(1-\beta)}{L} \right),\ \beta^{(\tau)}\equiv\beta\in(0, 1) $$
则:
$$ \min\limits_{0\leq k\leq \tau}\|\boldsymbol{\theta}^{(k+1)}-\boldsymbol{\theta}^{(k)}\|^2=O\left(\frac 1\tau \right) $$
由于$\eta^{(\tau)}$与$\beta^{(\tau)}$都是定值,我们可以认为序列$\{\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)}) \|^2 \}$的收敛速度同样是$O\left(\frac 1\tau \right)$。对于步长衰减的情况,此处不再赘述。
回头来看,好像只有在$\mathcal F_{\mu,L}^{2,1}$下HB对GD有加速效果,其他情况只是得到了同阶的收敛速度。此外,参考资料6值得一读,证明的技巧还是蛮巧妙的,在下一部分HB+SGD中也有用到。7、8就不推荐读了。
六、HB+SGD
现在我们探讨将HB方法应用于SGD上的收敛性能。我们已经有了SGD的基础了,那么SGD与GD相比,难点在于哪呢?就在于是用随机梯度$\boldsymbol{g}_{\tau}$的二阶矩。如果我们写成:$\boldsymbol{g}_{\tau}=\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)})+\boldsymbol{\delta}_\tau$,首先$\mathbb{E}[\| \boldsymbol{\delta}_{\tau}\|]=0$,而且我们可以自然地引入约束:
$$ \mathbb{E}[\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)}) \|^2]\leq G^2,\mathbb{E}[\|\boldsymbol{\delta}_{\tau} \|^2]\leq \delta^2\tag{7} $$
这样可以极大地简化证明的难度。在这一思路下,参考资料9分析了HB的收敛性能。但是它定理1、2的证明有严重问题,在求和的时候假设$\eta^{(\tau)}$是定值,然后求出结果后再令$\eta^{(\tau)}$为各种形式。现在我们自己动手来证明一下。
首先设$\mathcal L\in\mathcal F_{0,L}^{1,1}$,对于HB+SGD的原始形式(3),我们将其写为:
$$ \boldsymbol{\theta}^{(\tau+1)}+\boldsymbol{p}^{(\tau+1)}=\boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\frac{\eta^{(\tau)}}{1-\beta^{(\tau)}}\boldsymbol{g}_\tau,\ \boldsymbol{p}^{(\tau)}=\frac{\beta^{(\tau)}}{1-\beta^{(\tau)}}(\boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^{(\tau-1)})\tag{8} $$
假设我们已经有了$\boldsymbol{\theta}^{(0)},\boldsymbol{\theta}^{(1)}$,则上式从$\tau=1$开始迭代。两边减去$\boldsymbol{\theta}^*$再平方,我们有:
$$ \begin{align} &\mathbb{E}[\|\boldsymbol{\theta}^{(\tau+1)}+\boldsymbol{p}^{(\tau+1)}-\boldsymbol{\theta}^* \|^2] \\ =\ &\mathbb{E}[\|\boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\boldsymbol{\theta}^* \|^2]+\left(\frac{\eta^{(\tau)}}{1-\beta^{(\tau)}} \right)^2\mathbb{E}\left[\|\boldsymbol{g}_{\tau} \|^2\right] -\frac{2\eta^{(\tau)}}{1-\beta^{(\tau)}}\mathbb{E}\left[\left\langle \boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\boldsymbol{\theta}^*,\boldsymbol{g}_{\tau} \right\rangle\right]\\ \leq\ &\mathbb{E}[\|\boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\boldsymbol{\theta}^* \|^2]+\left(\frac{\eta^{(\tau)}}{1-\beta^{(\tau)}} \right)^2(G^2+\delta^2)\\ &-\frac{2\eta^{(\tau)}}{1-\beta^{(\tau)}}\mathbb{E}\left[\left\langle \boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^*,\boldsymbol{g}_{\tau} \right\rangle\right]-\frac{2\eta^{(\tau)}\beta^{(\tau)}}{(1-\beta^{(\tau)})^2}\mathbb{E}\left[\left\langle \boldsymbol{\theta}^{(\tau)}-\boldsymbol{\theta}^{(\tau-1)},\boldsymbol{g}_{\tau} \right\rangle\right]\tag{9}\\ \leq\ &\mathbb{E}[\|\boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\boldsymbol{\theta}^* \|^2]+\left(\frac{\eta^{(\tau)}}{1-\beta^{(\tau)}} \right)^2(G^2+\delta^2)\\ &-\frac{2\eta^{(\tau)}}{1-\beta^{(\tau)}}\mathbb{E}\left[ \mathcal L(\boldsymbol{\theta}^{(\tau)})-\mathcal L(\boldsymbol{\theta}^*)\right]-\frac{2\eta^{(\tau)}\beta^{(\tau)}}{(1-\beta^{(\tau)})^2}\mathbb{E}\left[\mathcal L(\boldsymbol{\theta}^{(\tau)})-\mathcal L(\boldsymbol{\theta}^{(\tau-1)}) \right]\tag{10}\\ \end{align} $$
其中(9)到(10)利用了凸性:
$$ \mathcal L(\boldsymbol{y})-\mathcal L(\boldsymbol{x})\geq \left\langle \nabla\mathcal L(\boldsymbol{x}),\boldsymbol{y}-\boldsymbol{x} \right\rangle\tag{10} $$
我们记:$\mathbb{E}[\|\boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\boldsymbol{\theta}^* \|^2]=A_\tau$,同时如果$\beta^{(\tau)}\equiv \beta\in(0,1)$,则:
$$ \begin{align} \tau\mathbb{E}[\epsilon(\tau)]\leq\ & \frac{1-\beta}{2}\sum_{k=1}^\tau \frac1{\eta^{(k)}}(A_k-A_{k+1})+\frac{\beta}{1-\beta}\mathbb{E}[\epsilon(0)]+\frac{G^2+\delta^2}{2(1-\beta)}\sum_{k=1}^\tau \eta^{(k)}\tag{11}\\ \leq\ & \frac{\beta}{1-\beta}\mathbb{E}[\epsilon(0)]+\frac{G^2+\delta^2}{2(1-\beta)}\sum_{k=1}^\tau \eta^{(k)}+\frac{1-\beta}{2}\left(\frac{A_1}{\eta^{(1)}}-\frac{A_{\tau+1}}{\eta^{(\tau)}} \right)\\ &+\frac{1-\beta}{2}\sum_{k=1}^{\tau-1}\left(\frac{1}{\eta^{(k+1)}}-\frac 1{\eta^{(k)}} \right)A_{k+1}\tag{12} \end{align} $$
如果我们进一步假设:$A_k\leq D^2$,所以:
$$ \tau\mathbb{E}[\epsilon(\tau)]\leq \frac{\beta}{1-\beta}\mathbb{E}[\epsilon(0)]+\frac{G^2+\delta^2}{2(1-\beta)}\sum_{k=1}^\tau \eta^{(k)}+\frac{(1-\beta)D^2}{2\eta^{(\tau)}}\tag{13} $$
取$\eta^{(\tau)}=\frac{c}{\sqrt{\tau}},c>0$,则:
$$ \begin{align} \mathbb{E}[\epsilon(\tau)]&\leq \frac{\beta\mathbb{E}[\epsilon(0)]}{(1-\beta)\tau}+\frac{(G^2+\delta^2)(2c\sqrt \tau-c)}{2(1-\beta)\tau}+\frac{(1-\beta)D^2}{2c\sqrt\tau}\\ &=\frac{2\beta\mathbb{E}[\epsilon(0)]-c(G^2+\delta^2)}{2(1-\beta)\tau}+\frac{2c^2(G^2+\delta^2)+(1-\beta)^2D^2}{2c(1-\beta)\sqrt\tau}\tag{14} \end{align} $$
上述证明与我们在优化器四:SGD的收敛性能中对一般凸函数的推导是一致的,都只运用了凸性,没有利用$L$-光滑。整理一下,我们有如下定理:
定理5:
若$\mathcal L\in\mathcal F_{0,L}^{1,1}$,且:
$$ \mathbb{E}[\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)}) \|^2]\leq G^2,\mathbb{E}[\|\boldsymbol{\delta}_{\tau} \|^2]\leq \delta^2,\mathbb{E}[\|\boldsymbol{\theta}^{(\tau)}+\boldsymbol{p}^{(\tau)}-\boldsymbol{\theta}^* \|^2]\leq D^2,\eta^{(\tau)}=\frac{c}{\sqrt{\tau}},c\geq \frac{2\beta\mathbb{E}[\epsilon(0)]}{G^2+\delta^2} $$
则:
$$ \mathbb{E}[\epsilon(\tau)]\leq\frac{2c^2(G^2+\delta^2)+(1-\beta)^2D^2}{2c(1-\beta)\sqrt\tau}=O(\frac{1}{\sqrt{\tau}}) $$
对于非凸的$L$-光滑情况,参考资料9给出了分析:
定理6:
若$\mathcal L\in\mathcal C_{L}^{1,1}$,且:
$$ \mathbb{E}[\|\boldsymbol{\delta}_\tau \|^2]\leq \delta^2,\|\nabla \mathcal L(\boldsymbol{\theta}) \|^2\leq G^2,\eta^{(\tau)}=\frac{c}{\sqrt\tau},c\leq \frac{1-\beta}{2L} $$
则:
$$ \min_{k=1,\cdots,\tau} \mathbb{E}[\|\nabla \mathcal{L}(\boldsymbol{\theta}^{(\tau)}) \|^2]\leq \frac{2(1-\beta)^4\epsilon(0)+c^2\big[L\beta^2(G^2+\delta^2)+L(1-\beta^2)\delta^2 \big]}{c(1-\beta)^3\sqrt\tau}=O(\frac{1}{\sqrt\tau}) $$
小结
关于HB的收敛性能就介绍到这里。有趣的是,我们一直在说动量加速,可事实上我们只在HB+GD在$\mathcal F_{\mu,L}^{1,1}$下证明了加速效果,还没有文献证明HB对SGD有加速效果,本文和其他的一些工作只取得了同阶或是稍慢一些的收敛速度。
关于HB,我们可以把它写成一种multi-stage的形式:
$$ \begin{cases} \boldsymbol{m}^{(\tau)}=\beta\boldsymbol{m}^{(\tau-1)}-\eta^{(\tau)}\boldsymbol{g}_{\tau} \\ \boldsymbol{\theta}^{(\tau+1)} = \boldsymbol{\theta}^{(\tau)} + \boldsymbol{m}^{(\tau)} \end{cases} $$
其中$\tau\geq 1,\boldsymbol{m}^{(0)}=\boldsymbol{\theta}^{(1)}-\boldsymbol{\theta}^{(0)}$。有的文献采用一种normalized形式:
$$ \begin{cases} \boldsymbol{m}^{(\tau)}=\beta^{(\tau)}\boldsymbol{m}^{(\tau-1)}-(1-\beta^{(\tau)})\boldsymbol{g}_{\tau} \\ \boldsymbol{\theta}^{(\tau+1)} = \boldsymbol{\theta}^{(\tau)} + \eta^{(\tau)}\boldsymbol{m}^{(\tau)} \end{cases} $$
在一些情况下取得了比原始形式下稍快一些的结果,如参考文献10。还有在非光滑、变$\beta$等情况下的分析,这里就不赘述了。
References
- http://www.cs.toronto.edu/~asamir/cifar/HFO_James.pdf
- https://blog.paperspace.com/intro-to-optimization-momentum-rmsprop-adam/
- Deep learning via Hessian-free optimization,James Martens,Proceedings of the 27th International Conference on Machine Learning(ICML 2010),2010
- Some methods of speeding up the convergence of iteration methods,Boris T. Polyak,USSR Computational Mathematics and Mathematical Physics,Volume 4 Issue 5 Pages 1-17,1964
- Introductory Lectures on Convex Optimization: A Basic Course,Yurii Nesterov,Springer Science & Business Media,2004
- **Global convergence of the Heavy-ball method for convex
optimization*,Euhanna Ghadimi et al*,2015 European Control Conference (ECC),2014 - Heavy-ball method in nonconvex optimization problems,Zavriev, S.K. and F.V. Kostyuk,Computational Mathematics and Modeling, 1993
- iPiano: Inertial Proximal Algorithm for Nonconvex Optimization,Peter Ochs et al,SIAM,2014
- Unified convergence analysis of stochastic momentum methods for convex and non-convex optimization,Tianbao Yang et al,arXiv preprint arXiv:1604.03257,2016
- An improved analysis of stochastic gradient descent with momentum,Yanli Liu,Proceedings of the 34th International Conference on Neural Information Processing Systems(NeurIPS),2020
